Data-Constrained Modelling of Material Microstructures and Properties

Although the X-ray CT and threshold image segmentation approach is widely used in the R&D community for sample-nondestructive (SND) characterization of internal microstructures of various materials [1], it is subjective and imposes an arbitrary length-scale cut-off at the X-ray CT voxel size. It generally assumes that each X-ray imaging voxel has a discrete material composition. That is, there are no finer structures smaller than the X-ray imaging voxels. The smallest X-ray CT voxel size is at the order 1/1000 of the sample size. In other words, the mainstream X-ray CT approach is inadequate to characterize material internal structures smaller than the order of 1/1000 of the sample size. This makes it not suitable for materials with multi-scale internal structures such as tight oil & gas reservoirs including shale, carbonate and tight sandstone; manufactured materials such as 3D-printed metal components, and corrosion inhibitive print primers [2-4]. As image segmentation is based on the X-ray CT slice image grey-scale, it is not sensitive enough to discriminate material compositions with similar X-ray attenuation properties.

The problem is addressed with the recent development in data-constrained modelling (DCM) method using quantitative X-ray CT [5,6]. By integrating statistical physics and multi-energy quantitative X-ray CT, DCM Video 1 explicitly reconstructs 3D microscopic distributions of materials and incorporates fine structures below X-ray CT image resolution as voxel compositional partial volumes. This offers a more accurate 3D representation of a material microstructure and enables more quantitative modelling of its properties. The DCM formulation will be presented in the next section, followed by a selection on case studies and references.

For DCM, a material sample is represented numerically on a simple cubic grid of N = N_x × N_y × N_z cubic vowels. On the nth voxel where n=1,2,.....,N, the DCM model minimizes the following objective function:

The problem is addressed with the recent development in data-constrained modelling (DCM) method using quantitative X-ray CT [5,6]. By integrating statistical physics and multi-energy quantitative X-ray CT, DCM Video 1 explicitly reconstructs 3D microscopic distributions of materials and incorporates fine structures below X-ray CT image resolution as voxel compositional partial volumes. This offers a more accurate 3D representation of a material microstructure and enables more quantitative modelling of its properties. The DCM formulation will be presented in the next section, followed by a selection on case studies and references.

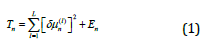
This is equivalent to minimize the discrepancy between the expected and the measured linear absorption coefficients and to maximize Boltzmann distribution probability [7]. In Equation (1), δμ_n^(l) is the difference between the expected and CT reconstructed linear absorption coefficients, and E_n is the dimensionless phenomenological interaction energy [5,8]. The optimization is achieved by adjusting the volume fraction variables V_n^(m) (m=0,1,....,M) for each material composition m, where M is the total number of non-void compositions, subject to the following constraints

Numerical solution to the above has been implemented as a DCM software [5,6]. Figure 1 is a typical main window of the DCM software. In DCM, sub-voxel structures are incorporated as coexistence of multiple compositions in the same voxels.

Figure 1: DCM software main display window for a case-study on cold-spayed Ti sample.

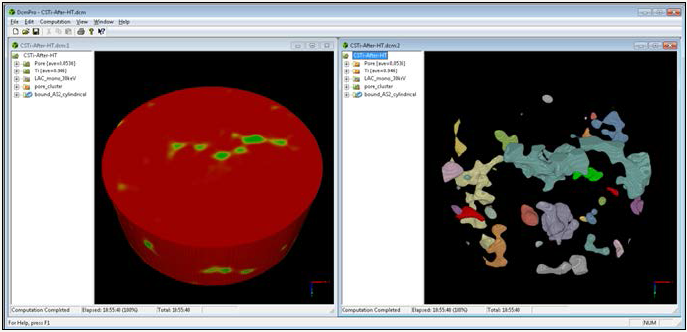
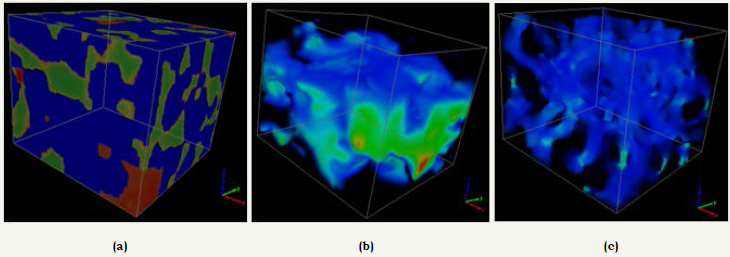
Figure 2: Microstructure and properties of a CIPS sandstone sample.

2a: Compositional distribution where quartz is displayed as blue, calcite as red and pores as green. Coexistences of multiple compositions in the same voxels are displayed as mixed colours.

_2b: Induced electric potential when the pores are filled with the sea water and an external potential difference is applied along the Z-axis.

_2c: Fluid speed distribution when a pressure difference is applied along the Z-axis.

As a demonstration case study for synthetic CIPS (Calcite Insitu Precipitation System) sandstone, which consists of quartz grains cemented by calcite, and pores? It was X-ray imaged at beam energies 35 and 45keV. The multi-energy X-ray datasets were analyzed using the DCM non-linear optimization algorithm [5]. The procedures of the analysis are demonstrated by the accompanying video https://research.csiro.au/static/dcm/DCM-CIPS-sandstoneweb- demo.mp4. Each voxel represents a sample volume of microns. Assuming the pores are filled with the sea water, its electrical conductivity and permittivity had been calculated using a finitedifference DCM plugin [9]. Its fluid permeability was calculated using a DCM plugin for partially percolating voxels [10,11]. Its composition distribution, induced voltage and fluid flow speed are illustrated in Figure 2.

1. Arns CH, Bauget F, Ghous A, Sakellariou A, Senden TJ, et al. (2005) Digital core laboratory: Petrophysical analysis from 3D imaging of reservoir core fragments. Petrophysics 46(4): 260-277.
2. Yang YS, Liu KY, Mayo S, Tulloh A, Clennell B, et al. (2013) A dataconstrained modelling approach to sandstone microstructure characterization. J Petroleum Science & Technology 105: 76-83.
3. Ren YQ, King PC, Yang YS, Xiao TQ, Chu C, et al. (2017) Characterization of heat treatment-induced pore structure changes in cold-sprayed titanium, Materials Characterization 132: 69-75.
4. Hughes AE, Yang YS, Hardin SG, Tulloh A, Wang Y, et al. (2015) Diversity of internal structures in inhibited epoxy primers. AIMS Materials Science 2(4): 379-391.
5. Yang YS, Trinchi A, Tulloh A, Chu C (2016) A tutorial introduction to DCM quantitative characterization and modelling of material microstructures using monochromatic multi-energy X-Ray CT, XRM 2014: Proceedings of the 12th International Conference on X-Ray Microscopy 1696: 02002.
6. Yang S, Chu C, Tulloh A, Chen F (2017) DCM-A Software platform for advanced 3D materials modelling, characterisation and visualization. CSIRO Data Access Porta.
7. Thompson CJ (1988) Classical equilibrium statistical mechanics, Clarendon Press, Oxford, UK.
8. Yang YS (2017) A data-constrained non-linear optimisation approach to a data-constrained model for compositional microstructure prediction. In Lecture Notes in Information Technology 15: 198-205.
9. Yang S, Tulloh A, Clennell B (201) A DCM plug-in for microstructurebased computation of material sample electric conductivity and permittivity. CSIRO Data Access Portal, Australia.
10. Li R, Chu C, Yang S, Pereira G (2017) DCM plugin for partially percolating LBM single phase flow. CSIRO Data Access Portal, Australia.
11. Li R, Yang YS, Pan J, Pereira G, Taylor J, et al. (2014) Lattice Boltzmann modeling of permeability in porous materials with partially percolating voxels. Phys Rev E Stat Nonlin Soft Matter Phys 90(3): 033301.