Investigation of Thermodynamic-Kinetics of Polyester Dyeing with Liquid Disperse Dye

Polyethylene terepthalate is one of the most important synthetic fibers used today. It is the most utilized polyester commercially [1]. It is a versatile fiber having wide applications in textiles like apparel, home furnishing textiles, technical textiles, to name a few. Also blends of polyester with natural or other synthetic fibers are used to a large extent. Disperse dyes are most widely used dyes mainly for coloration of polyester fibers along with other synthetic fibers [2]. It is well known that polyester fibers are dyed using disperse dyes at higher temperatures, generally at 130 °C [3]. Most commonly, the disperse dyes used today are azo and anthraquinone based. On majority basis, they are monoazo and anthraquinone based disperse dyes [2]. They are mostly used in the form of fine solid powder which consists of dispersing agent as an aid. The dispersing agent is introduced in the process of grinding during the manufacture of disperse dyes [4]. However, the process of grinding is time consuming and significantly contributes to the cost of finished dye powder since it is energy intensive. Therefore, it would be beneficial for the dyestuff manufacturing industries if alternative route is developed wherein above-mentioned demerits are eliminated. In these regards, manufacturing of disperse dyes without mechanical grinding in liquid form could be an enlightening approach. Furthermore, modern process houses use automatic color kitchen to prepare requisite dye solutions in liquid form. They are transported automatically from color kitchen to the dyeing machine. So, it would be of great practical convenience if the dye itself is supplied to the dyer in liquid form instead of solid. Also, the phenomenon of dusting of dyes gets eliminated in this case. Therefore, an attempt was made to prepare disperse dyes in liquid form directly from its crude press cake using a suitable solvent. Some solvents are reported to increase the yield of disperse dyeing [5]. The dyeing process of fibers and/or textiles gets divided into four consistent processes; diffusion of dye in the solution, adsorption at the fiber surface, diffusion into the fibre and fixation of the dye to the fibre. The diffusion of dye into fiber depends on pH, temperature and uses auxiliary agents as well [6].

The chemical reactions involved in dyeing processes can be better understood by studying the adsorption kinetics and thermodynamic parameters. The dyeing kinetics of polyester fibers by disperse dyes have been studied by several authors [7-11]. Various mathematical models have also been used [12-14]. The present communication investigates the possibility of application of disperse dyes in liquid form in terms of their thermodynamic and kinetic parameters like adsorption isotherm, partition coefficient, standard affinity, changes in enthalpy and entropy, diffusion coefficient, activation energy of the diffusion. The parameters of liquid form are compared vis-à-vis those of commercial form. This is a novel disperse dye formulation and not been sufficiently concentrated upon previously. From the results obtained, this novel product can offer a very promising alternative to the dyes industry.

Materials

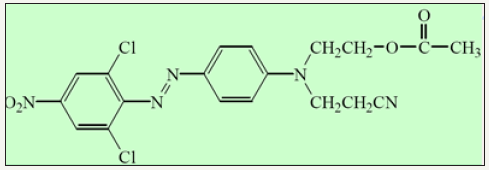
Ready for dyeing (RFD) polyester was procured from Tata Mills, (Mumbai, India). C. I. Disperse Orange 30 in crude form and commercial form was procured from Spectrum Dyes Pvt. Ltd. (Surat, India). The commercial form was used as obtained without further purification. The structure of C. I. Disperse Orange 30 is depicted in Figure 1. The lower homologue of polyethylene glycol (PEG) was of laboratory grade procured from S.D. Fine Chemicals Pvt. Ltd. All other chemicals and auxiliaries used were of laboratory grade procured from S.D. Fine Chemicals Pvt. Ltd. unless particularly mentioned.

Figure 1:CI Disperse orange 30.

Methods

Preparation of liquid form: Following formulation was used to prepare liquid form of crude dye;

Crude dye- 45-50%

Lower PEG homologue- 15-35%

Anionic dispersing agent- 20-40%

Water- balance

Total-100%

The formulation above was stirred by Remi Electrotechnik overhead stirrer for 24h at a speed of 1000rpm. After stirring, the solution was stored. This is the liquid form of crude disperse dye under consideration.

Dyeing equilibrium parameters:

A. Dye adsorption isotherm and partition coefficient

Adsorption isotherm gives the concentration of a substance adsorbed on a solid surface in relation to its concentration in the surrounding fluid when the system is at equilibrium at a constant temperature [2]. The Nernst isotherm is the simplest, given by the Equation (1).

C_f is the concentration of dye in fiber at equilibrium, C_s is concentration of dye in dye bath at equilibrium and K is a constant called as partition coefficient [2]. From the graph of C_f against C_s, Nernst isotherm can be determined from the slope of which, the partition coefficient K, can be obtained.

The Langmuir isotherm follows the Equation (2).

Cmax is the maximum number of adsorption sites that dye molecules can occupy in the fiber. From the graph of C_f/C_s against C_s, Langmuir isotherm can be obtained [2]. The Freundlich isotherm is described by the Equation (3).

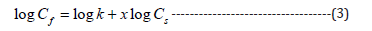
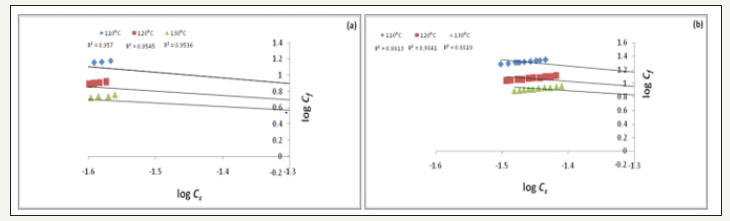
where, x is the exponent.

From the graph of log C_f against log C_s, the Freundlich isotherm can be determined [2,12]. To establish dye adsorption isotherm and study thermodynamic and kinetic parameters, dyeing process was carried out in a Flexi Dyer dyeing machine. Before dying, the fabric samples were scoured using 2g/l non-ionic surfactant at 60 °C for 30min. The temperatures used for dyeing were 110, 120 and 130 °C until equilibrium adsorption was obtained. The equilibrium was achieved within 3-4h depending on experimental conditions. To assure the achievement of equilibrium, experiments were prolonged at the desired temperatures for 5h. The material to liquor ratio used was 1:10,000 which could be considered as infinite liquor ratio. The pH was maintained at 4.5 during dyeing. After dyeing the samples were washed with cold acetone and dried [15]. The experimental data obtained were subjected to analyses for determination of adsorption isotherms. The equations of Nernst, Langmuir and Freundlich isotherms were applied. The best correlation coefficient would determine the adsorption isotherm. Also, the partition coefficients of dye between dyebath and the fiber were determined at different temperatures.

B. Standard affinity

The most basic thermodynamic parameter is the standard affinity (-Δμo) of the dye in dyeing solution towards fiber substrate. Standard affinity is an important quantitative measure of the tendency of dye to pass from one phase to the other [16]. This parameter was defined as a difference between the chemical potential of the dye in the fiber and the chemical potential of the dye in the dyeing solution. It is the measure of tendency of a dye to move from its standard state of solution to its standard state of fiber [17].

The standard affinity (-Δμo) of a dye can be calculated using Equation (4).

-Δμo, standard affinity (cal/mol); μ_f^o, standard chemical potentials of dye in a fiber; μ_s^o, standard chemical potentials of dye in a solution; R, gas constant (1.9872cal/mol K); T, absolute temperature (K); C_f, dye concentration in a fiber (mol/kg); C_s, dye concentration in a solution (mol/L); and K, partition coefficient.

C. Enthalpy change

For enthalpy calculation, Equation (5) was used. The enthalpy change can be obtained from the slope of graph of -Δμ_o/T against 1/T.

ΔH^o, heat of dyeing (cal/mol); -Δμ_o, standard affinity (cal/mol); T, absolute temperature (K); and C, integral constant.

D. Entropy change

The entropy change was calculated using Equation (6).

-Δμo, standard affinity (cal/mol); ΔHo, heat of dyeing (cal/mol); ΔSo, change in entropy (cal/mol.K); and T, absolute temperature (K).

E. Diffusion parameters

Diffusion coefficient

According to Equation (7), the diffusion coefficient was calculated from the plot that shows the relationship between Ct/Ceq and t1/2 at the initial stage of dyeing.

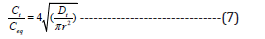
Ct, dye exhaustion at a time (t) (mol/kg); Ceq, dye exhaustion at the equilibrium (mol/kg); Dt, diffusion coefficient (cm2/min); and r, radius of fiber (cm).

t1/2 was calculated using Equation (8)

F. Activation energy of the diffusion

Using Equation (9), the activation energy of diffusion was calculated from the relationship between ln D and 1/T

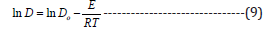
D, diffusion coefficient at a temperature T (cm2/min); Do, constant; E, activation energy; R, gas constant (1.9872 cal/mol.K); and T, absolute temperature (K).

G. Adsorption extent of dye on the fiber

The dye concentration in the dye bath was measured using Techcomp 8500 UV-visible spectrophotometer. Calibration was obtained using properly diluted stock solutions of dye. To grant validity of Beer’s law, N,N-dimethylformamide (DMF) was used as a solvent [18]. The dye concentration within the fiber was measured by extracting dye from fibers in boiling DMF and concentration of the extracted dye was measured using spectrophotometer.

Adsorption isotherm and standard affinity

The adsorption isotherms of C. I. Disperse Orange 30 in commercial form as well as in liquid form are shown in Figures 2-4. The equations of Nernst, Langmuir and Freundlich isotherms were applied to the data. It is well established that disperse dyeing of polyester follows solid solution theory. Thus, dye gets distributed in the dyebath and the fabric. This distribution is influenced by partition coefficient. This is the basic premise of Nernst isotherm and was reflected in the correlation coefficients. The best correlation coefficient was found for Nernst isotherm. Thereafter, partition coefficient was obtained from the Nernst isotherm. The partition coefficient values are summarized in Table 1.

Table 1:The partition coefficient (K) and standard affinity (-Δμo) of C. I. disperse orange 30 in commercial and liquid forms.

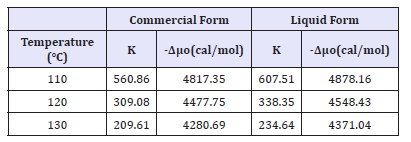
Figure 2:Nernst adsorption isotherm (a) Commercial form; (b) Liquid form.

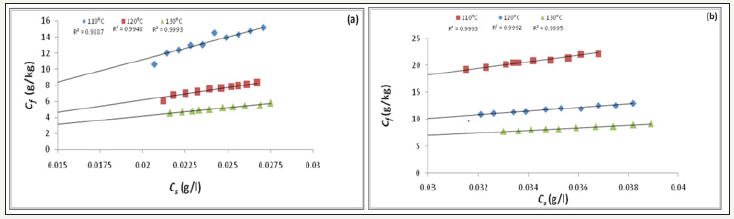
Figure 3:Langmuir adsorption isotherm (a) Commercial form; (b) Liquid form.

Figure 4:Freundlich adsorption isotherm (a) Commercial form; (b) Liquid form.

The partition coefficient of the liquid form of C. I. Disperse Orange 30 was found to be higher than corresponding partition coefficient of its commercial form. This clearly suggests that more dye gets transferred from dyebath to the fabric in case of liquid form. As temperature increases, the partition coefficient decreases for both forms of the dye. As dyeing is an exothermic reaction, the partition coefficients can be negatively affected by higher dyeing temperatures. From the partition coefficients, standard affinity was obtained using Equation (4). The standard affinity values are depicted in Table 1. Standard affinity is an indicative parameter of tendency of the dye molecules to get transferred from liquid phase to the solid phase. Standard affinity of liquid form is higher than that of the corresponding value of commercial form. This reflects the potential of liquid form to transfer higher amount of dye from liquid phase to solid phase than commercial form. That is, the tendency of the dye molecules for moving from its standard state in the dyebath to its standard state in the fiber is higher in case of liquid form.

Enthalpy and entropy changes

Figure 5:Plots of -Δμo/T against inverse of temperature (1/T) for computation of enthalpy change (a) Commercial form; (b) Liquid form

The adsorption of dye onto fibers is an exothermic process and releases heat energy [19]. Obviously, the dyeing conditions, such as types of fibers, dyes and the dyeing media affect the amount of released heat of dyeing. In fact, the enthalpy change in the dyeing system shows the amount of exothermic energy arising out of interaction between the polymeric chains of fiber and dye. Therefore, the enthalpy change is primarily considered as the measure of the adsorption strength of dyes [20]. Figure 5 demonstrates the linear relationship between (-Δμo/T) and (1/T) on the enthalpy change as shown in Equation (4). The enthalpy and entropy values for both the forms are depicted in Table 2.

Table 2:The enthalpy change (ΔHo) and entropy change (ΔSo) of C. I. Disperse orange 30 in commercial and liquid forms.

The enthalpy change for the liquid form is higher than that of the commercial form. This confirms that the adsorption of dye is higher in case of liquid form. The entropy change shows the extent of the reduced freedom of dye molecules after the completion of dyeing process. The negatively larger value of the entropy change represents the phenomenon that the mobility of the dye molecules is decreased after dyeing [16]. The entropy change for the liquid form is marginally higher in magnitude than the commercial form. Thus, it can be deduced that the decrease in the mobility of dye molecules after dyeing is comparable for both the forms.

Diffusion coefficient and activation energy of the diffusion

The dyeing process generally involves three continuous steps. The first step is the diffusion of dye through the aqueous dye bath onto the fiber. The second step is the adsorption of dye into the outer layer of the fiber. The last step is the diffusion of dye into the fiber matrix from the adsorbed surface. The second step, the actual adsorption process, is generally assumed to be much more rapid than either of the other diffusion steps. Of the two diffusion steps, the diffusion into the inner layer is much slower than the movement of dye through the aqueous solution due to the physical obstruction of dye diffusion presented by the network of fiber molecules for the dye molecules to diffuse into the fiber. It is expected that the free volume could be formed within the substrate. This free volume is regarded as the void being temporarily formed within the polymers by the thermal movement of molecular chains and the dye molecules penetrate such empty space [20]. Diffusion coefficients are summarized in Table 3.

Table 3:The diffusion coefficient (D) of C. I. Disperse orange 30 in commercial and liquid forms.

There is an increase in the diffusion coefficient with increase in temperature for both the forms of dye. As the temperature increases the strike rate of the dye also increases thereby increasing the mobility of the dye molecules in the bath and the fiber structure. The activation energy of the diffusion can be calculated using Equation (9) that is known as the Arrhenius equation. This parameter describes the dependence of the diffusion coefficient on the dyeing temperature and represents the energy barrier that a dye molecule should overcome to diffuse into the polymer molecules [21]. The activation energy of the diffusion can be obtained from the slope in the linear relationship between ln D and 1/T shown in Figure 6.

Figure 6:Plots of ln D against 1/T for computation of activation energy of the diffusion (a) Commercial form; (b) liquid form.

Table 4:The activation energy of the diffusion (ED) of C. I. Disperse orange 30 in commercial and liquid forms.

The calculated activation energy is presented in Table 4. The activation energy of the diffusion is less in the case of liquid form as compared to the commercial form. This suggests that dye molecule must overcome less energy barrier to diffuse into polymer molecule in liquid form than in commercial form.

Thermodynamic and kinetic parameters of commercial form and liquid form of C. I. Disperse Orange 30 were deeply investigated. The dyeing reactions for both the forms followed Nernst adsorption isotherm. Distribution coefficients were higher for liquid form demonstrating higher dye transfer than commercial form. The standard affinity of liquid form to polyester was also greater than that of commercial form to polyester indicating higher apparent depth of dyeing of liquid form on transfer of dye from dye bath to the fiber. Higher negative value of the enthalpy change was observed for liquid form than commercial form. On the other hand, the entropy change for both the forms was almost the same. There was an increase observed in diffusion coefficients with increase in temperature for both the forms. The activation energy of commercial form was higher than that of liquid form. From the study performed, it can be concluded that this novel route of manufacturing disperse dyes in liquid form introduces a potential economical alternative to the dyes industry.

Authors would like to express their gratitude to UGC for fellowship and consumable grant.

1. Fourné F (1999) Synthetic fibres, machines and equipment manufacture, properties. Hanser Publishers, Germany, p. 67.
2. Broadbent A (2001) Basic principles of textile coloration. Society of Dyer’s and Colourists, pp.1-579
3. Shore J (2002) Colorants and auxiliaries organic chemistry and application properties. Society of Dyers and Colourists, p 134.
4. Hunger C (2003) Industrial dyes chemistry, properties, application. Wiley-VCH, Germany, p. 134.
5. Nunn D (1979) The dyeing of synthetic-polymer and acetate fibres. Dyes company publications trust, p. 131.
6. Ujhelyiova A, Bolhova E, Oravkinova J, Tino R, Marcin A (2007) Dyes Pigm. 72: 212.
7. Peters R (1975) The physical chemistry of dyeing. Textile chemistry, Elsevier Scientific Publishing Company, p. 143.
8. Crank J (1968) Diffusion in polymers. Academic Press, London, UK.
9. Wang P, Ma J (1998) Dyes Pigm. 37: 121.
10. Etters J (1994) Textile Chemist and Colorist. 26: 17.
11. Park K, Koncar V (2004) AUTEX Research Journal. 4: 45.
12. Vickerstaff (1954) The physical chemistry of dyeing. Oliver and Boyd, London, UK, p. 90.
13. Cegarra J, Puente P (1967) Textile Research Journal. 37: 343.
14. Bird C (1975) The theory of coloration of textiles. In: Peters L (Ed.), The dyers company publications trust. England, p. 241.
15. Kim T, Son Y, Lim Y (2005) Dyes Pigm. 67: 229.
16. Vickerstaff (1954) The physical chemistry of dyeing. Oliver and Boyd, London, UK, p. 100.
17. Johnson A (1989) The theory of coloration of textiles. (2nd edn), Society of Dyers and Colorists, West Yorkshire, p. 255.
18. Golob V, Tusek L (1999) Dyes Pigm. 40: 211.
19. Navid R, Mohammad K, Seyed A, Maryam R (2012) Dyes Pigm. 94: 386.
20. Weigmann H (1977) Textile Research Journal. 47: 745.
21. Johnson A (1989) The theory of coloration of textiles. (2nd edn), Society of Dyers and Colorists, West Yorkshire, p. 396.