On Bubble Regeneration and Broadening with Implications for Decompression Protocols

Definitions and Acronyms

Standard (SI) and English units are employed. By convention, by usage or for ease, some nonstandard units are employed. Pressure and depth are both measured in feet-of-sea-water (fsw) and meters-of-sea-water (msw) with 1atm=33fsw=10msw to good approximation. Also used for scale lengths of bubbles are micron with 1micron=10−6m. Acronyms are employed herein. They are standard:

I. ANDI: Association of Nitrox Diving Instructors.

II. BM: Bubble phase model dividing the body into tissue compartments with halftimes that are coupled to inert gas diffusion across bubble film surfaces of exponential size distribution constrained in cumulative growth by a volume limit point.

III. Bubble broadening: Noted laboratory effect that small bubbles increase, and large bubbles decrease in number in liquid and solid systems due to concentration gradients that drive material from smaller bubbles to larger bubbles over time spans of hours to days.

IV. Bubble regeneration: Noted laboratory effect that pressurized distributions of bubbles in aqueous systems return to their original non-pressurized distributions in time spans of hours to days.

V. CCR: Closed circuit rebreather, a special RB system that allows the diver to fix the oxygen partial pressure in the breathing loop (setpoint).

VI. CMAS: Confederation Mondial des Activates Subaquatiques.

VII. Critical radius: Temporary bubble radius at equilibrium, that is, pressure inside the bubble just equals the sum of external ambient pressure and film surface tension.

VIII. DB: Data bank storing downloaded computer profiles in 5-10sec time-depth intervals.

IX. DCS: Crippling malady resulting from bubble formation and tissue damage in divers breathing compressed gases at depth and ascending too rapidly.

X. Decompression stop: Necessary pause in a diver ascent strategy to eliminate dissolved gas and/or bubbles safely and is model based with stops usually made in 10fsw increments.

XI. Deep stop: Decompression stop made in the deep zone to control bubble growth.

XII. DAN: Divers Alert Network.

XIII. Diveware: Diver staging software package usually based on USN, ZHL, VPM and RGBM algorithms mainly.

XIV. Diluent: Any mixed gas combination used with pure oxygen in the breathing loop of RBs.

XV. Diving algorithm: Combination of a gas transport and/or bubble model with coupled diver ascent strategy.

XVI. DOD: Department of Defense.

XVII. DOE: Department of Energy.

XVIII. Doppler: A device for counting bubbles in flowing blood that bounces acoustical signals off bubbles and measures change in frequency.

XIX. DSAT: Diving Science and Technology, a research arm of PADI.

XX. DSL: Diving Safety Laboratory, the European arm of DAN.

XXI. EAHx: Enriched air helium breathing mixture with oxygen fraction, x, above 21% often called helitrox.

XXII. EANx: Enriched air nitrox breathing mixture with oxygen fraction, x, above 21%.

XXIII. EOD: End of dive risk estimator computed after finishing dive and surfacing.

XXIV. ERDI: Emergency Response Diving International.

XXV. FDF: Finnish Diving Federation.

XXVI. GF: Gradient factor, multiplier of USN and ZHL critical gradients, G and H, that try to mimic BMs.

XXVII. GM: Dissolved gas model dividing the body into tissue compartments with arbitrary half times for uptake and elimination of inert gases with tissue tensions constrained by limit points.

XXVIII. GUE: Global Underwater Explorers.

XXIX. Heliox: Breathing gas mixture of helium and oxygen used in deep and decompression diving.

XXX. IANTD: International Association of Nitrox and Technical Divers.

XXXI. ICD: Isobaric counter diffusion, inert dissolved gases (helium, nitrogen) moving in opposite directions in tissue and blood.

XXXII. IDF: Irish Diving Federation.

XXXIII. LSW theory: Lifschitz-Slyasov-Wagner Ostwald bubble ripening theory and model.

XXXIV. M-values: Set of limiting tensions for dissolved gas buildup in tissue compartments at depth.

XXXV. Mirroring: The gas switching strategy on OC ascents of reducing the helium fraction and increasing the oxy-gen fraction in the same amount thereby keeping nitrogen constant.

XXXVI. Mixed gases: Combination of oxygen, nitrogen and helium gas mixtures breathed underwater.

XXXVII. NAUI: National Association of Underwater Instructors.

XXXVIII. NDL: No decompression limit, maximum allowable time at given depth permitting direct ascent to the surface.

XXXIX. NEDU: Naval Experimental Diving Unit, diver testing arm of the USN in Panama City.

XL. Nitrox: Breathing gas mixture of nitrogen and oxygen used in recreational diving.

XLI. OC: Open circuit, underwater breathing system using mixed gases from a tank exhausted upon exhalation.

XLII. Ostwald ripening; large bubble growth at the expense of small bubbles in liquid and solid systems.

XLIII. OT: Oxtox, pulmonary and/or central nervous system oxygen toxicity resulting from over exposure to oxygen at depth or high pressure.

XLIV. PADI: Professional Association of Diving Instructors. XLV. PDE: Project Dive Exploration, a computer dive profile collection project at DAN.

XLVI. Phase volume: Surfacing limit point for bubble growth under decompression.

XLVII. RB: Rebreather, underwater breathing system using mixed gases from a cannister that are recirculated after carbon dioxide is scrubbed with oxygen from another cannister injected into the breathing loop. recreational diving: air and nitrox nonstop diving.

XLVIII. RGBM algorithm: An American bubble staging model correlated with DCS computer outcomes by Wienke.

XLIX. RN: Royal Navy.

L. SDI: Scuba Diving International.

LI. Shallow stop: Decompression stop made in the shallow zone to eliminate dissolved gas.

LII. SI: Surface interval, time between dives.

LIII. SSI: Scuba Schools International.

LIV. TDI: Technical Diving International.

LV. Technical diving: Mixed gas (nitrogen, helium, oxygen),

OC and RB, deep and decompression diving.

LVI. TMX x/y: Trimix with oxygen fraction, x, helium fraction, y, and the rest nitrogen.

LVII. Trimix: Breathing gas mixture of helium, nitrogen and oxygen used in deep and decompression diving.

LVIII. USAF: United States Air Force.

LIX. USCG: United States Coast Guard.

LX. USN: United States Navy.

LXI. USN algorithm: An American dissolved gas staging model developed by Workman of the US Navy.

LXII. UTC: United Technologies Center, an Israeli company marketing a message sending-receiving underwater computer system (UDI) using sonar, GPS and underwater communications with range about 2 miles. VPM algorithm: an American bubble staging model based on gels by Yount.

LXIII. Z-values: Another set of limiting tensions extended to altitude and similar to M-values.

LXIV. ZHL algorithm: A Swiss dissolved gas staging model developed and tested at altitude by Buhlmann.

Introduction

Bubble birth, growth, evolution, destruction and elimination in the body of human divers are central issues in safe diver staging protocols from exposures at depth. Today, despite incredible technological advances in medical and physiological science, we really know very little about bubbles in vivo and their complex behavior under pressure and environmental changes. Measuring bubbles and their properties in vivo by invasive means often destroys or changes what is being measured. Measuring with noninvasive techniques is very limited. Doppler scoring of moving body bubbles is only able to count numbers. Experiments using materials with properties like blood and tissue can be useful as a starting point for simulating bubble behavior but of course blood and tissue are metabolic and perfused adding additional complexity and unknowns to coupled modeling and simulation. In this vein, therefore, we investigate bubble data and experiments in the laboratory to make some hypothetical estimates of possible impacts of bubble regeneration and broadening on diver staging regimens. We emphasize these are speculative based on experiments in the laboratory not in the field nor in divers. The fact that tissue and blood are both perfused and metabolic always throws wrenches into biophysical modeling. Simple rheological assignments of laboratory variables and physical constants doesn’t necessarily extrapolate to divers.

We take up bubble regeneration and broadening in model frameworks and experiments are briefly re-counted. Diving models are detailed, and features of the models impacted by regeneration and broadening are quantified. Comparative results for real diving are given in each case. Cases include OC and RG mixed gas diving in decompression and no decompression scenarios. Comparative results across these cases will be seen to be small to moderate for nominal exposures. Nonetheless, it is still important to spell out the techniques used to address bubble regeneration and broadening in general. To accomplish this, models (USN, ZHL, VPM, RGBM) are delineated with specific model constructs addressing bubble regeneration and broadening underscored. The starting points for model alterations are the permissible supersaturations which vary across and within USN, ZHL, VPM and RGBM staging protocols codified next. This analysis represents a first time ever estimate of hypothetical bubble regeneration and broadening impacts on decompression staging protocols within dissolved gas (GM) and bubble (BM) models.

Model Frameworks

Two well-known classes of models, dissolved gas (GM) and bubble (BM), are implemented and safely utilized in modern dive computers, diveware and dive tables. The USN [1] and ZHL [2] models are GM algorithms and stage ascents by requiring that dissolved gas limit points, called M, are never exceeded at any point on the ascent. The VPM and RGBM models are both BM algorithms. The VPM [3] and RGBM [4] are BM algorithms and stage ascents by requiring that excited bubble volumes, ϕ , never exceed a limit point, called the phase limit, Φ on surfacing. Both GM and BM models assign tissue compartments, τ , which quantify dissolved gas buildup and elimination during a dive. BM models also couple dissolved gas to bubbles by diffusion across bubble-tissue interfaces.

In all models, tissue compartments, τ , are first defined and span a range for both nitrogen and helium,

and dissolved gas tensions, p, for buildup and elimination in time, t, follow the well-known tissue equations for nitrogen and helium independently,

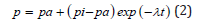
for pi initial tensions and pa ambient pressures for each species. The constant, λ, takes the usual form,

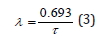
and helium, τ He, and nitrogen, τ N2, halftimes related by Graham’s law for bulk diffusion,

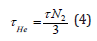
The total gas tension, Π, is the sum of helium, pHe, and nitrogen, pN2, components,

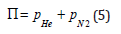
in each tissue compartments. Ambient partial pressures, pa, are simple functions of gas fractions, breathing mixture and depth, d, at sea level, that is, in fsw or msw,

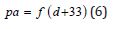
for fHe and fN2. Thus, in the tissue equations, nitrogen and helium exhibit different gas exchange properties. After this, GM and BM models diverge in staging regimens. GM staging algorithms rely on limit points to dissolved gas buildup and elimination while BM algorithms couple dissolved gas to diffusion across bubble interfaces and rely on separated bubble volumes to stage divers. Critical to all models is the permissible supersaturation permitted on the ascent and that is where bubble regeneration and broadening enter the staging protocols. The permissible supersaturations for the USN, ZHL, VPM and RGBM models, denoted G, H, X and Y respectively, follow.

Dissolved Gas Models (GM)

GM algorithms typically bring divers into the shallow zone for decompression (shallow stops). Ascent rates are nominally a slow 30fsw/min. Critical tensions, M, have little to nothing to do with actual bubble formation in the tissue and blood but are (statistical) medical limit points to observed nonstop diving outcomes using arbitrary tissue compartments, τ . The approach dates to Haldane and the 1900s and has been used extensively since then with little change and some tweaking of values. Much testing by World Navies has ensued on the medical side. Notable are the USN and ZHL models as follow:

USN model [1]

In the Workman USN approach, the permissible gas tension, Π, (nitro-gen plus helium) is limited by,

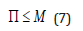
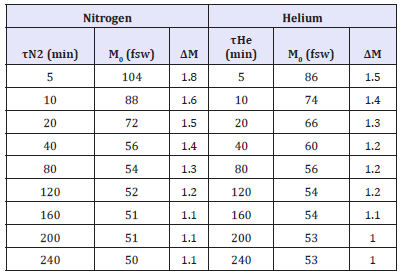
with M critical tensions listed in Table 1 for depth, d,

Table 1:Workman USN M-Values.

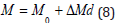
where depth, d, is the difference between total ambient pressure, P, and surface pressure, P0,

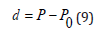
Corresponding permissible gradients, G, then satisfy,

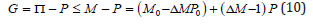
with P0 ambient pressure at the surface,

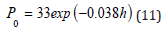
for elevation, h, in multiples of 1000ft. Bubble regeneration and broadening affect G and M to follow.

ZHL model [2]

The Buhlmann ZHL approach was tested at low altitude and is like the Workman USN approach, that is, the permissible gas tension, Π (nitrogen plus helium again), is limited by fit parameters, a and b, lumped in Table 2,

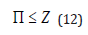
Table 2:Buhlmann swiss Z-values.

with critical tensions, Z, given by,

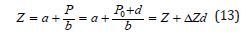
with,

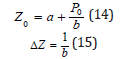
Accordingly, we have, critical gradient, H,

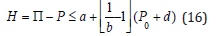
for constants, a and b, defining Z at sea level (P0=33fsw) in Table 2. The expressions put the ZHL Z-value model in the same computational framework as the USN M-value model. As with the USN model, H and Z will be affected by bubble regeneration and broadening.

Bubble Models

Similarly, BM algorithms are used across recreational and technical diving on both OC and RB systems. Technical divers mostly rely on BM algorithms or constructs called gradient factors (GF) which multiply M and Z values in GM approaches to mimic BM behavior in decompression diving. Staging starts in the deep zone and continues into the shallow zone (deep stops). Ascent rates are also 30fsw/min. Bubbles are assumed using empirical properties and exponential distributions in size but have never been really measured in humans. The phase volume limit point, Φ , is also deduced and fitted from diver exposure profiles using data from the LANL Data Bank within statistical correlations of bubble model and exposure data. Testing is nowhere near as extensive as dissolved gas approaches but is growing. The model relies on correlations with actual mixed gas diving across OC and RB, deep and decompression diving on arbitrary breathing mixtures. Application and use are growing, particularly in the technical diving sector over the past 20-25 years, with new computers implementing bubble models. In particular, the VPM and RGBM models are noteworthy and used extensively within recreational and technical diving sectors as follow:

Varying permeability model [3]

The tissue compartments in the Yount VPM for nitrogen consist of the set,

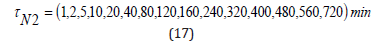
with the helium compartments scaling,

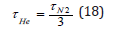
The VPM model links to bubble experiments in gels and related strata. In gel experiments, Yount separated gas diffusion across bubble interfaces into permeable and impermeable regions. For dive applications, the regions separate around 165fsw. Bubbles of nitrogen and helium are excited into growth by pressure changes during the dive from some minimum excitation radius, ε₀ , in the 0.6-micron range, with nitrogen bubbles slightly larger than helium bubbles and the excitation radius decreasing with increasing absolute pressure, P. The excitation radius separates growing from shrinking bubbles. The radial bubble distribution, n, in the VPM is given by,

with n0 an experimental normalization factor for gel sample size and β on the order of 1/ε micron−1 for diving applications. The staging protocol in the VPM limits the permissible supersaturation, X to prevent bubble growth on ascent,

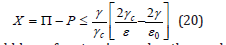
with γ the bubble surface tension and γc the crushing bubble surface tension, roughly 20dyne/cm and 150dyne/cm respectively. The critical radius, ε0, is an experimental metric, somewhere near 0.7 micron for both nitrogen and helium. For diving, VPM ascents are limited by W at each stage in the decompression and staging profiles are iterated to convergence across all stops. The effects of bubble regeneration and broadening in the VPM are tagged by changes to X and ε0 as will be seen and compared.

Reduced gradient bubble model [5]

Nitrogen tissue compartments in the Wienke RGBM range,

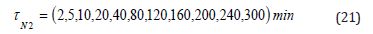
with helium compartments,

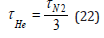
The bubble dynamical protocol in the RGBM model amounts to staging on the minimal seed number averaged, free-dissolved gradient, Y, across all tissue compartments for P permissible ambient pressure, Π total inert gas tissue tension, n excited bubble radial distribution (exponential), γ bubble surface tension and r bubble radius,

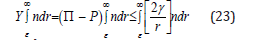
so that,

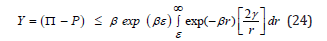
for ε the excitation radius at P, that is, for nitrogen

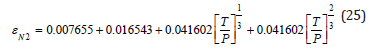
and helium,

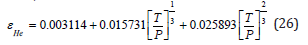
for T measured in absolute temperature, oK, and P in the usual diving pressure metric, fsw. Time spent at each stop is iteratively calculated so that the total separated phase, φ, is maintained at, or below, its limit point, Φ . This requires some computing power but is attainable in diver wrist computers presently marketed with the same said for the VPM. The USN and ZHL models are less complex for computer implementation. The limit point to phase separation, Φ , is near 600 micron3 and the distribution scaling length, β, is close to 0.60 micron−1 for both nitrogen and helium. Both excitation radii, ε, and surface tension, γ, are functions of ambient pressure and temperature and not constant. The equation-of-state (EOS) assigned to the bubble surface renders the surface tension below lipid estimates, on the order of 20dyne/cm and excitation radii are below 1 micron.

Well known USN, ZHL, VPM and RGBM algorithms implemented across a majority of marketed and tested dive computers, diveware and tables have seen widespread and safe usage [5,6] over many years with GM computers around since the 1970s and BM computers more recent and gaining in popularity since the 1990s especially in the technical diving community. With extensive computer implementations and safe utilization record without noted DCS nor oxtox spikes and staging issues, they can be considered user validated across nominal recreational and technical diving. It is also reasonable to assume they can and will be safely modified to accommodate diving beyond the envelope in the future.

Bubble Dynamics

Most questions of seed distributions, lifetimes, persistence and origins in the body are unanswered today. And while we have yet to measure microbubble distributions and lifetimes in the body, we can gain some insight from laboratory measurements and statistical mechanics. Microbubble distributions have been studied extensively. The biophysics work [7-13] details some interesting studies about microbubbles and properties in general and follows in abbreviated form.

Microbubbles typically exhibit size distributions that decrease exponentially in radius, r. Holography measurements of cavitation nuclei in water tunnels suggest,

with,

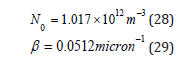
Experiments in gels also display exponential dependences in cavitation radii,

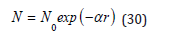
with,

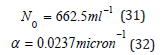
Both MRI and Doppler laser measurements of water and ice droplets in the atmosphere underline exponential decrease in number density as droplet diameter increases. Ice and water droplets in clouds typically range, 2micron≤r≤100micron. Dust and pollutants are also exponentially distributed, potentially serving as heterogeneous nucleation sites. It might be a surprise if micronuclei in the body were not exponentially distributed in number density versus size.

Lifetimes of cavitation voids are not known, nor measured, in the body. The radial growth equations provide a framework for estimation using nominal blood and tissue constants. Consider first the mass transfer equation,

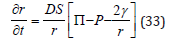
with all quantities as before, that is, r bubble radius, D diffusivity, S solubility, γ surface tension, P ambient pressure and Π total gas tension. The time to collapse, τ, can be obtained by integrating over time and radius, taking initial bubble radius, ri,

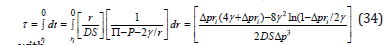
with,

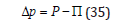
If surface tension is suppressed, we get,

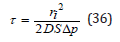
In both cases, small tension gradients, p and small transport coefficients, DS, lead to long collapse times and vice-versa. Large bubbles take a longer time to dissolve than small bubbles. Taking nominal transport coefficient for nitrogen, DS=56.9×10−6micron2/ secfsw, and initial bubble radius, ri=10.0 micron, for

Δp = 3.0 fsw and γ=40dynes/cm, we find

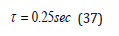
In the Rayleigh-Plesset picture [11,13], the radial growth equation takes the form, neglecting viscosity,

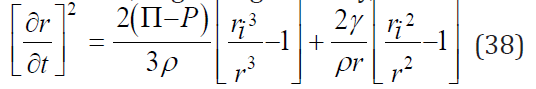
so that the collapse time by diffusion only is,

with,

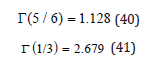
Suppressing the diffusion term in the growth equation, there similarly obtains,

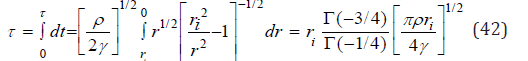
with,

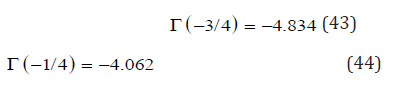
Collapse time in the Rayleigh-Plesset picture is linear in initial bubble radius, ri and inversely proportional to the square root of the tension gradient, p, or the surface tension, γ. Taking all quantities as previously, with density, ρ=1.15g/cm3, we find with surface tension suppressed,

and, for the diffusion term suppressed with only the surface tension term contributing,

Dissolution times above range,

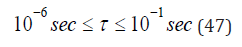
In the Yount model of persistent nuclei, within the permeable gas transfer region, seed nuclei lifetimes, τ, range,

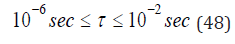
The collapse rate increases with both γ and p and inversely with ri. Small bubbles collapse more rapidly than large bubbles, with large bubble collapse driven most by outgassing diffusion gradients and small bubble collapse driven most by constrictive surface tension. Between these extrema, both diffusion and surface tension play a role. In any media, if stabilizing material attaches to micronuclei, the effective surface tension can be reduced considerably, and bubble collapse arrested temporarily, that is, as γ → 0 as a limit point. For small bubbles, this seems more plausible than for large bubbles because smaller amounts of material need adhere. For large bubbles, bubble collapse is not aided by surface tension as much as for small bubbles, with outgassing gradients taking longer to dissolve large bubbles than small ones. In both cases, collapse times are likely to lengthen over the short times estimated above. Additionally, external influences on the bubble, like crevices and surface discontinuities, may prevent bubble growth or collapse. All this adds to bubble complexities faced by modelers. The questions of regeneration and broadening are equally complex and follow.

Bubble Regeneration and Diving Implications

It is known that samples of knox gelatin, fingerling salmon and albino rats [7-9] display increased resistance to bubble formation following rapid application of bubble crushing pressures. The larger the com-pression pressures, the fewer bubbles that form with the same allowed supersaturation during decompression. Bubble models assume that gas nuclei are crushed by the mechanical strength of an initial compression and that the number of nuclei larger than the critical radius, ε, decreases. Presumably, surfactant molecules are forced out of the bubble skin into a possible reservoir outside where they remain available to retake their old positions in the bubble distributions. This is also the reason to make first dives deepest and subsequent dives shallower than the previous. While this has not been proven nor tested in the diver per se, it forms a plausible background to take a look at bubble regeneration effects in diver decompression staging.

It has also been shown theoretically [10] at equilibrium that the radial distribution of bubble nuclei is exponential and that a nuclear population, once crushed, stochastically restores itself over time scales of minutes to hours to days. This effect is seen every day in reactor coolants, bubble column processes, high speed flows and high temperature chemical reactions [11]. The higher the flow rates and temperatures, the shorter the regeneration times. In boiling water reactors for instance, regeneration times are in the 10sec range. Stationary decompressed gels in the laboratory exhibit long regeneration times of days. Bubble regeneration over varying time and size scales is seen in surf and breaking waves [12]. It seems that rapidly moving, turbulent and high temperature environments more readily support regeneration because of increased collisional dynamics and material disruption. The diver by comparison seems an unlikely candidate but perhaps tribonuncleation processes in tissue and blood [13] are strong enough to initiate bubble regeneration too. Nothing is presently known about possible regeneration times in humans and divers and the assumption has been that regeneration times are long compared to dive times. We will look at bubble regeneration effects on diver staging protocols for both short and long times. The time span for bubble regeneration in bubble models is a crucial element in calculations of NDLs and decompression staging.

USN and ZHL

Right off the bat, of course, USN and ZHL are dissolved gas models and not bubble models. But using the same techniques that were employed in the recreational RGBM [4,11] in defining bubble reduction factors as multipliers for critical tensions, M and Z, and permissible gradients, G and H, we can estimate reductions due to bubble regeneration in GMs. These reduction factors, ζ, take the form of critical tension multipliers all less than 1. Resulting reductions in critical tensions will then reduce NDLs and increase decompression staging times. The process is a bootstrap of reductions in the full RGBM to make pseudo-bubble regeneration in GMs just like the short SI, deeper-than-first and multiday diving fractions in the recreational RGBM implemented in meters, software and tables. The bubble model regeneration simulations next up obviously were performed first before any bootstrapping of the USN and ZHL algorithms. This is a little work, of course, and has been done before.

Therefore, after RGBM bootstrapping we take the gradient multiplier, ζ, as a measure of bubble redistribution reduction on critical parameters, M and Z, G and H, over time, t, in the range,

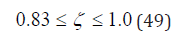
so that in the USN case,

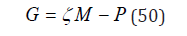
and for the ZHL,

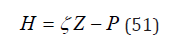
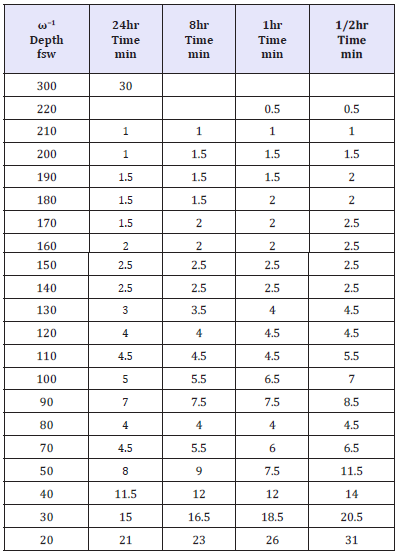
With ω−1 the time scale for bubble regeneration, we have in dive time, t,

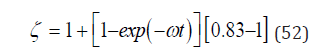
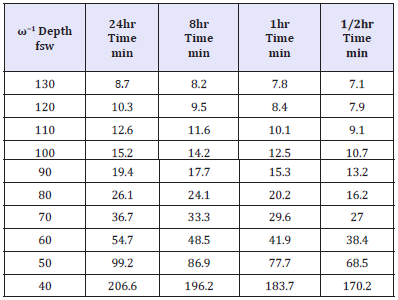
Comparative results follow in Table 3 which lists air NDLs with regeneration for ω−1 varying from 1 day down to 1/2hr using the USN model. The NDL reductions are small to moderate at depth but large in the shallower zones. The longer the regeneration time scale, ω−1, the lesser reduction in NDLs. For regeneration time scales roughly beyond 4hrs effects are relatively small and unimportant especially at increasing depth. Similar results obtain using BMs like VPM and RGBM as GMs and BMs converge for nonstop diving [13- 20].

Table 3:Air NDLs and regeneration.

VPM and RGBM

Dynamics described hold within the VPM with gel parameters and the RGBM with EOS fits in lipid and aqueous materials [11]. Both employ the similarity relationship for the equilibrium (surface) distribution excitation radius, ε0, and the crushed distribution excitation radius, εm, at depth as a function of ambient

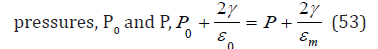
with P0 and ε0 surface values and P and εm values at depth. This relationship imparts bubble crushing at depth thereby yielding larger excitation radii, εm, than surface excitation radii, ε0. Larger excitation radii lead to decreased NDLs and longer decompression stop times. Possible regeneration during dive time, t, permits the crushed distribution to return to the equilibrium state within time spans, ω−1, such that excitation radii in time, ε(t), evolve from the relaxation relationship,

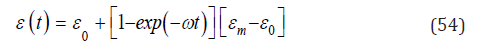
with similarity relationship then recast,

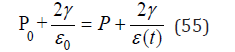
Table 4 tabulates decompression times for a 16/14 trimix dive down to 300fsw for 30min with a stop for 2min at 160fsw and switch to 20/10 trimix and another switch at 80fsw to EAN50 using the RGBM and assuming the critical radii, εm, relax over time scales, ω−1, The increases in decompression time are moderate too large for this extreme exposure when regeneration time scales, ω−1, drop into the 4-8hr range. Gel experiments do not suggest 1hr regeneration times, so we depart here for illustrative purposes.

Table 4:Decompression schedules for 16/14 trimix dive and regeneration.

Bubble Broadening and Diving Implications

Bubble broadening is a phenomenon observed by Ostwald [14] in 1897 whereby small bubbles diminish in size and large bubbles grow over time spans of hours to days. Concentration gradients (diffusion) drive the transport of material across bubble interfaces with small bubbles at higher concentrations than large bubbles because of their increased curvature and surface tension pressure. An everyday example is the re-crystalization of water within ice cream which gives old ice cream a gritty, crunchy texture. Larger ice crystals grow at the expense of smaller ones within the ice cream creating a coarser surface texture.

A systematic theory of bubble broadening developed by Lifshitz et al. [15] (LSW) suggests in supersaturated and solid solutions that the distribution mean bubble radius, rm, evolves in time as,

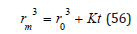
with r0 the unbroadened initial mean radius and K the transport coefficient a function of temperature, bubble surface tension, diffusivity, gas solubility and gas molar volume. For a wide range of experiments [16] the relationship holds with the transport coefficient, K, varying across materials of course. Two experiments of interest include the Kabalnov [17] and Del Cima studies. In the Kabalnov [17] fluorocarbon experiments, the LSW transport coefficient, K, was determined,

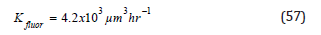
for the emulsion. Rheological scaling suggests the extrapolation to body blood and tissue,

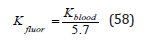
with,

In the Del Cima [18] glycerol-water studies, Kglycerol deviated from the LSW value,

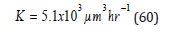
according to,

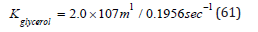
with,

and the fitted bubble number, nb, and distribution mean radius, rm, in time t, in a glycerol-water suspension were then given by,

for t in hrs and rm in micron (10−6m). Glycerol-water suspensions again are not blood and the transport coefficient in glycerol is empirically 1/7.8 the value in blood. To use the fitted expression from glycerol we then take for tissue and blood,

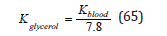
as an approximation. Other representations in different materials with rheological scaling will also be investigated in the future and the Kabalnov [17] study is sufficient here.

USN and ZHL

Analogous to the regeneration multipliers in GMs, bubble broadening multipliers can be introduced to reduce critical tensions, M and Z, and permissible supersaturations, G and H, with the same effects on NDLs and decompression staging times, that is, reduced NDLs and increasing decompression time. The procedure is the same as in the regeneration case but with different scaling and parameters. Accordingly, we bootstrap the reduction factors, χ, in the GMs to the NDL results of the full RGBM for assumed bubble broadening. Then as in the regeneration case, we take the critical tension multiplier, χ, as a measure of bubble broadening with commensurate reduction in M and Z plus G and H over dive time, t,

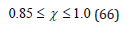
so that in the USN case,

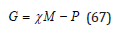
and for the ZHL,

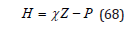
with ω−1 the time scale for bubble broadening. Time scale, ω−1, is again the crucial factor in the multipliers, χ. The evolution in dive time, t, is assumed over the range of χ above,

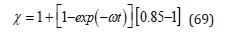
Using the multipliers, χ, in the ZHL, Table 5 tabulates broadening for a heliair (21/79 heliox or EAH21) CCR dive to 420fsw for 15min with setpoint 1.1atm. This is not an easy dive by any means, technical or otherwise.

Table 5:Decompression schedules for 420fsw CCR Divewith broadening.

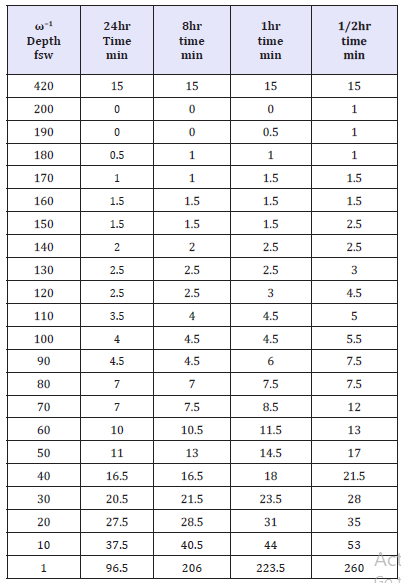
The schedule is a typical GM dissolved gas protocol with most time spent in the shallow zone. The broadening effects are large in the shallow zone for this extreme heliox CCR dive. Beyond 8hrs broadening time scales, ω−1, hypothetical effects are small. The same profile run with BMs exhibits the usual deeper stops and shorter run times [13] by about 10% to 16% with broadening effects similarly small beyond 8hrs broadening time scales.

VPM and RGBM

In bubble models, the excitation radii, ε, are central to the staging regimen. A simple approach to broadening is to require the integrals of the unbroadened and broadened distributions from excitation radius to ∞ to be equal. This obviously just scales the distributions to the excitation radii while conserving growing bubble numbers. The distributions are assumed to be exponential. The process is straightforward as follows.

Normalizing the initial distribution of bubbles to the unbroadened mean radius, r0, and the final distribution of bubbles to the broadened mean radius, rm, we have,

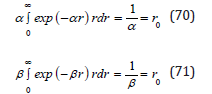
To find the broadened critical radius, εm, in terms of the unbroadened radius, ε0, we set the normalized integrals from critical radii to equal, thereby conserving growing bubble numbers,

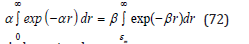
which yields in lowest order,

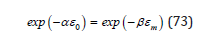
so that,

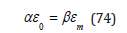
and the new critical radii, εm, in the VPM and RGBM obtain by simple scaling of the initial critical radii, ε0, by the ratio of broadened, rm, to unbroadened, r0, distribution mean radii,

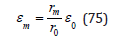
A higher order approximation scheme equates the integrals of growing bubbles over radius, r, that is

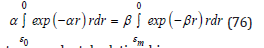
yielding a transcendental relationship

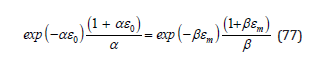
which is solvable numerically. The correction to the low order approximation is small and neglected herein.

Finally, as Doppler counting peaks in an hour or so suggesting bubble washout and since LSW bubble broadening increases linearily in time, the RGBM (and VPM) broadened critical radius, εm, is modulated with a relaxation time, ω−1, such that over dive time, t, the new modulated critical radius, ε(t), is given by,

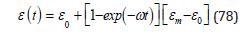
with relaxation halftime roughly 4hrs,

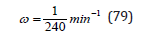
Modifications described hold for the VPM with gel parameters while the RGBM relies on fits in lipid and aqueous materials [14]. Both employ the similarity relationship,

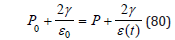
with P0 and ε0 surface values and P and ε(t) values at depth. This relationship imparts bubble crushing at depth thereby yielding larger excitation radii, ε(t), than surfacing excitation radii, ε0. The critical radius, ε(t), is then modulated over relaxation scales, ω, as described. The above relationship is also a staging criterion limiting ambient pressure, P, as a function of excitation radii, ε(t). Effects on three decompression dives on trimix and air with switches on the way up follow.

Table 6:Decompression schedules for 16/14 trimix dive and broadening.

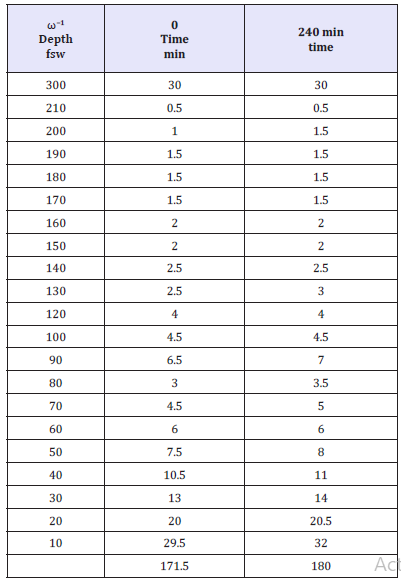
Table 6 tabulates decompression times for a deep 16/14 trimix dive down to 300fsw for 30min with a stop for 2min at 160fsw and switch to 20/10 trimix and another switch at 80fsw to EAN50 using RGBM and broadening time scale bottom time. Differences are small increasing slightly in the shallow zone for this deep decompression dive. This dive on OC is not a simple dive considering the depth, bottom time and gas switching on the way up. Decreasing the helium fraction and increasing the oxygen fraction in the same amount on the way up is called mirroring and is a useful technique that keeps nitrogen roughly constant for decompression and with partial pressures below narcosis thresholds.

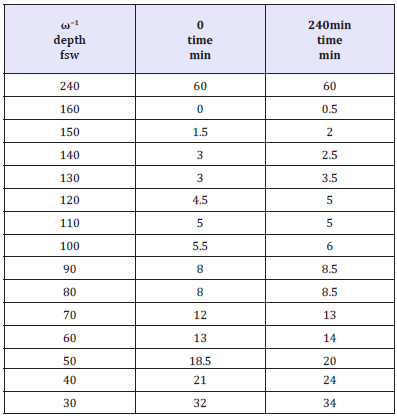
Table 7 tabulates decompression times for an air dive down to 240fsw for 15min using the VPM with switches to EAN20 at 80fsw and EAN50 at 30fsw with broadening time scale decompression plus bottom time. This is a easy technical dive compared to the previous trimix dive. Differences here are in the noise because bottom time is small. As dive times and depth increase broadening effects increase obviously. Effects show up more strongly for very extreme diving and diving on the envelope but certainly outside recreational and technical regimes. Beyond 8hrs broadening time scales effects are small. But if we extend the bottom time to 60min effects are notable as seen for the same dive in Table 8 with the VPM and the same broadening time scale. The increase in overall decompression time in both cases reminds that decompression debt accrues rapidly with increasing depth and exposure time. Broadening effects in this case increase decompression time by roughly 10%. Longer bottom times permit larger hypothetical bubble broadening.

Table 7:Decompression schedules for 240fsw short air dive and broadening.

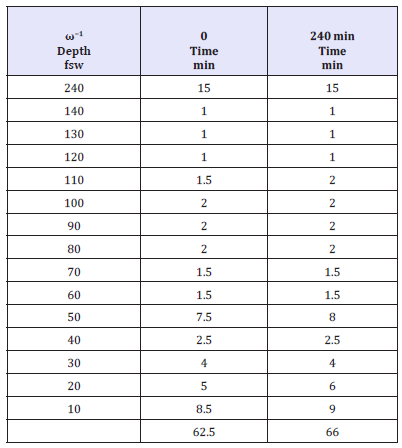
Table 8:Decompression schedules for long 240fsw air dive and broadening.

Summary

We have presented a hypothetical study of possible impacts of bubble regeneration and broadening on diver staging using empirical laboratory data and tests. A framework was constructed and detailed for assessing effects within well established and safe diving models, namely USN, ZHL, VPM and RGBM. The effects impacting NDLs and decompression staging times are relatively small for nominal recreational and technical diving but increase in magnitude as exposure times and depth increase and regeneration and broadening folding times decrease. None of the regeneration nor broadening effects have been seen nor measured in actual divers and likely will not be soon. However, we have given a computational framework to investigate such effects and their impacts on diving and dive operations. Hopefully that is of interest to diving organizations as a useful research and operational tool in the future. This was a first time ever analysis of possible diver staging modifications due to bubble regeneration and broadening. Bubble broadening is seen in many systems and particularly hydrocarbon ensembles but extrapolations of rheological variables to use results are highly suspect. Lipid and aqueous proteins in the body are known to be surfactants in body bubbles and change the properties of bubbles making them different from simple rheological extensions of experiments. In Doppler studies and bubble scoring, bubble washout for nominal (safe) diving completes in an 4hrs or so, peaking around 1hr. So, whatever is happening with regeneration and broadening it seems it wouldn’t last long since the number of Doppler bubbles flowing in the diver is decreasing rapidly. In these hypothetical simulations, regeneration and broadening time scales beyond 4hrs or so only effect diver staging times mildly.

Some organizations with concerns herein include the training agencies (NAUI, PADI, GUE, IANTD, TDI, IDF, FDF, CMAS, ANDI, SSI to mention a few), commercial diving industry (Schlumberger, Halliburton, Baker-Hughes, Exon-Mobil, Weatherford just a few more), meter manufacturers (Suunto, Mares, Huish, Atomic Aquatics, Cochrane, Shearwater, Cressisub, UTC, Oceanic, Sherwood, Ratio and others), software purveyors (GAP, ABYSS, DecoPlanner, ProPlanner, Free Phase, VPlanner, DiveLogger, Analyst), military and civilian diving operations (USN, USMC, USAF, DHS, EPA, etc), medical researchers and data collectors (DAN, DSL, NEDU, NOAA, NASA, EPA) and related professional organizations (ADA, etc). It is hoped that this analysis is helpful in their planning, research and operations. A listing of modern dive computers and diveware is compiled in the Appendix for the interested reader as well as training models used by diver training agencies. The analysis presented can be easily incorporated into meters, tables and diveware as well as ad-hoc operational procedures in training regimens.

Targeted impacts of this analysis of bubble broadening effects on diver staging, meters, diveware tables, models and training standards are numerous. The following are representative vehicles and diver training outlets.

Commercial Units

The number of dive computers marketed has grown significantly in the past 20 years or so. A representative cross section of commercial units presently marketed is listed. Units incorporate both GM and BM protocols. These units are modern and engineered for performance and safety. Most have PC connectivity and dive planning software along with interfaces to DAN and LANL DBs for profile downloading. The record of all is one of safe and extensive real-world diving under many environmental conditions. All are amenable to implementation of bubble regeneration and broadening and include:

A. Suunto Suunto markets a variety of computers using the RGBM. The EON Steel and DX can be used in gauge, air, nitrox, trimix, OC and CCR modes. The D6, D4 and Vyper are OC computers in gauge, air and nitrox modes. The Zoop and Cobra are recreational computers for gauge, air and nitrox use.

B. Mares All Mares computers use the RGBM. Recreational models include the ICON HD, Matrix, Smart and Puck Pro for OC in gauge, air and nitrox modes.

C. Uwatec Uwatec computers are marketed by ScubaPro and all use the ZHL algorithm. The M2 and Pro Mantis are targeted for both recreational and technical diving with gauge, air, nitrox, trimix and CCR modes. The Pro Galileo Sol is a technical dive computer with gauge, air, nitrox and trimix capabilities.

D. UTC UTC markets a message sending-receiving computer called the UDI for air and nitrox. All UDIs employ the RGBM. The message exchanging capabilities extend out to 2 miles using sonar, GPS and underwater communications systems. Models include the UDI 14 and UDI 28. Underwater special military units, search and recovery teams and exploration operations use the UDIs routinely today. UDIs also have high resolution compasses for extended navigation.

E. Huish/Atomic Aquatics/Liquivision Huish Outdoors owns both Atomic Aquatics and Liquivision. Atomic Aquatics markets a recreational dive computer using the RGBM called the Cobalt for air and nitrox. Liquivision models include the Kaon, Lynx, X1 and Xeo. The Lynx and Kaon are technical and recreational computers for gauge, air and nitrox modes using the ZHL with GFs. The X1 and Xeo are full up technical dive computers for air, nitrox, trimix and CCR using offering both the ZHL with GFs and RGBM.

F. Cressisub All Cressisub computers use the RGBM in recreational gauge, air and nitrox modes. The Newton Titanium. Goa, Giotta and Leonardo are Cressisub models. Cressisub markets a complete line of diving gear in addition to dive computers.

G. Sherwood Sherwood computers all use the ZHL. Recreational models for air and nitrox include the Amphos and Wisdom computers.

H. Oceanic Oceanic computers use the DSAT and ZHL algorithms for recreational diving. Many models are marketed for gauge, air and nitrox diving and include the VTX, Datamax, Geo, Pro Plus. OCi, Atom, Veo and F10.

I. Shearwater Shearwater computers are targeted for technical diving. All use the ZHL with GFs and VPM may be downloaded as an option, The Petrel, Perdex and Nerd2 models address air, nirox, trimix and CCR. Some RB Manufacturers are integrating Shearwater computers into their RB units.

J. Ratio Ratio computers employ the ZHL and VPM algorithms for technical and recreational diving. Models include the iX3M Pro and IX3M GPS (Easy, Deep, Tech+, Reb versions) plus the iDive Sport and iDive Avantgarde (Easy, Deep, Tech+ versions) series with air, nitrox, helium and CCR capabilities and GPS and wireless connectivity. The model list is impressive and complete with a strong offering of technical and professional diving units.

K. Cochrane Cochrane computers are marketed for recreational and technical diving using the USN LEM (VVAL18). The EMC16 a is recreational air and nitrox computer. The EMC20H is a technical air, nitrox and helium unit. Military units include the EODIII for USN EOD operations and the NSWIII for USN Special Warfare (SEAL) evolutions.

L. Aeris Aeris computers are directed at recreational divers using DSAT (modified USN) algorithms for air and nitrox. Models include the A100, A300, A300AI, XR1, NXXR2, Elite T3, Epic and Manta.

Most dive computers are manufactured by one of 4 companies, namely Seiko, Timex, Citizen and Casio, certainly a storied and well-known group of fine instrument makers to be sure. Many are backed up with dive planning software (diveware) described next.

Diveware

A number of popular dive planning software packages are also amenable to direct implementation of this analysis. Online and commercially available software packages span GM and BM algorithms along with oxtox estimation and include:

a. Free Phase RGBM Simulator Free Phase RGBM Simulator is a software package offered by Free Phase Diving incorporating the ZHL and RGBM algorithms. Both the ZHL and RGBM algorithms are user validated and correlated with actual diving data and tests as mentioned. The Free Phase RGBM Simulator for nominal settings is one-to-one with the published and released NAUI Technical Diving Tables [20-22] used to train mixed gas OC and RB divers. As such, it is a valuable training and diving tool for deep and decompression diving. No other diveware packages, excepting NAUI GAP and ANDI GAP, provide such correlation with published and user validated Dive Tables. It is also keyed to the Liquivision RGBM implementation plus a few others under construction in the Far East.

b. Abyss Abyss in the mid-90s first introduced the full RGBM into its diveware packages. The Buhlmann ZHL model was also included in the dissolved gas package. It has seen extensive use over the past 20 yrs or so in the technical diving area. A variety of user knobs on bubble parameters and Z-values permit aggressive to conservative staging in both models. Both the ZHL and RGBM have been published and formally correlated with diving data. Later, the modified RGBM with χ was incorporated into Abyss. Modified RGBM with χ was published and correlated with data in the late 90s and also served as the basis for Suunto, Mares, Dacor, ConnXion, Cressisub, UTC, Mycenae, Aqwary, Hydrospace, ANO, Artisan and other RGBM dive computers. Full RGBM was first incorporated into Hydrospace computers and today in Suunto, Atomic Aquatics, Liquivision and ANO computers.

c. VPlanner VPlanner first introduced the VPM in the late 90s. Based on the original work of Yount and Hoffman, the software has seen extensive use by the technical diving community. Formal LANL DB correlations of the VPM and thus VPlanner have been published [22]. User knobs allow adjustment of bubble parameters for aggressive to conservative staging. VPlanner is also used in Liquivision and Advanced Diving Corporation computers for technical diving.

d. ProPlanner ProPlanner is a software package that uses modified Z-values for diver staging. Buhlmann Z-values with GFs are employed with user knobs for conservancy. The model is called the VGM ProPlanner by designers. Some GFs claim to mimic the VPM. Correlations have not been formally published about VGM and ProPlanner.

e. GAP GAP is a software package similar to Abyss offering the full RGBM, modified RGBM with χ and Buhlmann ZHL with GFs. Introduced in the mid 90s, it has seen extensive usage in the recreational and technical sectors. Apart from user GFs, the models and parameters in GAP have been published and correlated with diving data and profiles tested over years. Adjustable conservancy settings for all models can be selected. GAP has been keyed to Atomic Aquatics and Liquivision dive computers. Training Agency spinoffs also include ANDI GAP and NAUI GAP.

f. DecoPlanner DecoPlanner is a diveware package offered by the GUE Training Agency. Both the VPM and Buhlmann ZHL with GFs are available in DecoPlanner. Evolving over the past 10- 15yrs, DecoPlanner also incorporates GUE ratio deco (Π/P≤ξ ) approaches to modifying GFs. Nothing is published about ratio deco data correlations but both the ZHL and VPM have been correlated [20-22]. It has seen extensive use in the technical diving community and GUE diver training.

g. Analyst Analyst is a software package marketed by Cochrane Undersea Technology for PCs. It is keyed to Cochrane computers as a dive planner and profile downloader. The Cochrane family of computers use the USN LEM for recreational, technical and military applications. The LEM is a neo-Haldanian model with exponential uptake and linear elimination of inert gases. It is part of the massive USN VVAL18 project.

h. DiveLogger DiveLogger is linked to Ratio technical and recreational computers. Ratio computers provide GPS and wireless connectivity and offer the ZHL and VPM algorithms to divers. Dive planning and profile downloading capabilities are included in the diveware package. As mentioned, both VPM and ZHL have been correlated with data.

i. DiveSim DiveSim is an UDI software package for dive planning and profile downloading. UDI computers and diveware employ the correlated RGBM for air and nitrox. The software packages also include diver to diver, diver to surface, GPS, compass and related communications capabilities. UDIs are obviously highly technical and useful underwater tools used by military, search and rescue and exploration teams but are readily accessible to recreational divers needing underwater communications and boat connectivity.

j. DRA A similar development from Dan Europe (DSL) is the Diver Safety Guardian (DSG) software package providing the diver with feedback from an online Deco Risk Analyzer (DRA). Based on per-missible gradients, it is under testing and development. An EOD risk estimator now, plans are in the works to make it a wet (OTF) risk estimator.

k. CCPlanner CCPlanner is a LANL software package offering full RGBM, modified RGBM, USN M-value and Buhlmann Z-value algorithms for dive planning. It is used by the C&C Team and is not distributed commercially but is obtainable under written contract. A risk analysis routine using the LANL DB is encoded in CCPlanner and imbedded in licensed RGBM OC and RB codes.

Training Agency Testing and Standards

Some Agencies have conducted wet tests and implemented their own protocols into training regimens formally or optionally (NAUI, PADI, GUE, TDI, ANDI, IANTD). This is described in the Deep Stop Work-shop Proceedings [21]. Prior to the introduction of deep stops Training Agencies relied on GM approaches in training divers and instructors with successful and safe results. The ZHL and USN table and computer implementations were mainstays in their training. When deep stop protocols entered the training scene in the 1990s, some Agencies (rather quickly) adopted a look and see attitude while applying their own testing and modified training regimens to BM algorithms, mostly VPM and RGBM. Without DCS and oxtox issues with deep stops, deep stop training standards were then drafted and implemented. As far as training regimens go, the following summarizes training standards for some well know US Agencies:

i. NAUI: a recreational and technical Training Agency using RGBM tables, meters and linked software

ii. PADI: a recreational and technical Training Agency using DSAT tables, meters and software with deep stop options

iii. SSI: a recreational Training Agency using modified USN tables

iv. ANDI: a technical Training Agency using RGBM table, meters and diveware

v. SDI/TDI/ERDI: a recreational and technical Training Agency using USN tables, computers and com-mercial diveware

vi. IANTD: a recreational and technical Training Agency employing the ZHL and VPM tables, computers and software

vii. GUE: a technical Training Agency that uses ZHL and VPM tables, computers and software

Training Agencies using USN and ZHL protocols for technical instruction often couple GFs (gradient multipliers) to dive planning software for modifications to standard protocols. Some using tables have modified times and repetitive groups to be more conservative. CMAS affiliated Training Agencies are free to choose their tables, meters and software for training and diving. FDF and IDF employ RGBM tables, meters and software. An important thing here to mention is that regardless of training standards, tables, meters and software, Agencies safely train divers and rely on well known, safe and accepted protocols. Their record is admirable.

Acknowledgment

Thanks to our friends and colleagues at LANL, NAUI, C&C Dive Team Operations, DAN, Commercial Diving Industry, recreational and technical Training Agencies, Computer Manufacturers worldwide and many collaborators at Universities, National Laboratories, DOE, DOD, USAF, USCG and USN.

Bio Sketches

Bruce Wienke is a Program Manager in the Weapons Technology/Simulation Office at LANL. He received a BS in physics and mathematics (Northern Michigan), MS in nuclear physics (Marquette) and a PhD in particle physics (Northwestern). He has authored 350+ articles in peer reviewed journals, media outlets, trade magazines, workshop proceedings and has published 12 books on diving science, biophysics and de-compression theory. He heads up the C& C Dive Team vested with worldwide underwater search, assessment and disablement of nuclear, chemical and biological WMDs. He is a Fellow of the APS, Technical Committee Member of the ANS, Member of the UHMS and serves as a Consultant to the EPA, DHS, ADA, US Military and Dive Industry. Bruce is an Editor/Reviewer for CBM, PR, TTSP, NSE, JQSRT and CEO of Southwest Enterprises Consulting. He is the developer of the Reduced Gradient Bubble Model (RGBM) implemented in decompression meters, tables and dive software worldwide. Bruce has dived all over the world on OC and RB systems in military, scientific, exploration, testing and training activities. He is a NAUI Tec/Rec Instructor Trainer and Course Director. Interests include USSA Masters ski racing, USTA Seniors tennis, golf and windsurfing. Bruce is a Certified Ski Instructor (PSIA) and Racing Coach (USSCA). He has won Masters National Titles in SL, GS, SG and DH and Quarterbacked the Northern Michigan Wildcats to a NCAA II Title in the Hickory Bowl.

Tim O’Leary heads up NAUI Technical Diving Operations having developed and co-authored training manuals, support material, tech dive tables, monographs and related media along with Tech Course Standards. He is a practicing commercial diver and CEO of American Diving & Marine Salvage on the Texas Gulf Coast. Tim received a BS in zoology (Texas A&M) and a DMT and CHT from Jo Ellen Smith Medical Center at the Baromedical Research Institute. He was a Commercial Diving and Hyperbaric Chamber Instructor at the Ocean Corporation. Tim is a member of the UHMS, SNAME and NADMT. He is an Admiral in the Texas Navy, a USCG 100 Ton Vessel Master and a Consultant to Texas Parks & Wildlife, Canadian Corporation, Rimkus Group and Offshore Oil Industry. His diving experience is globalon OC and RB systems in commercial, exploration, training and testing activities. He is a NAUI Tec/Rec Instructor Trainer, Course Director and Workshop Director. Other interests include skiing, deep wreck diving, and dive travel. Tim and NAUI Dive Team are credited with the discovery and exploration of the USS Perry in approximately 250fsw off Anguar and diving it for a week on RBs.

Appendix

Meters, Diveware, Tables and Training Agencies

References

1. Workman RD (1965) Calculation of decompression schedules for nitrogen-oxygen and helium-oxygen dives. USN Experimenal Diving Unit Report, Washington DC, USA.
2. Buhlmann AA (1984) Decompression: Decompression sickness. Springer-Verlag Publishing, Berlin, Germany.
3. Yount DE, Hoffman DC (1986) On the use of a bubble formation model to calculate diving tables. Aviat Space Environ Med 57(2): 149-156.
4. Wienke BR (1990) Reduced gradient bubble model. Int J Biomed Comp 26(4): 237-246.
5. Bennett PB, Wienke BR, Mitchell S (2008) Decompression and the deep stop workshop. UHMS/NAVSE Proceedings, Salt Lake City, USA.
6. Wienke BR, O’Leary TR (2016) Diving bubble model data correlations. J Marine Sci Res Dev 6(4): 1000204.
7. Wienke BR (2018) Dive computer profile data and on the fly and end of dive risk estimators. J Appl Biotech Bioeng 5(1): 00118.
8. Yount DE, Strauss RH (1976) Bubble formation in gelatin: A model for decompression sickness. J Appl Phys 47: 5081-5089.
9. Yount DE, Gillary EW, Hoffman DC (1984) A microscopic investigation of bubble formation nuclei. J Acoust Soc Am 76: 1511-1521.
10. Yount DE, Yeung CM, Ingle FW (1979) Determination of the radii of gas cavitation nuclei by filtering gelatin. J Acoust Soc Am 65: 1440-1450.
11. Yount DE (1982) On the evolution, generation and regeneration of gas cavitation nuclei. J Acoust Soc Am 71: 1473-1481.
12. Wienke BR (2015) Science of diving. CRC Press, Boca Raton, USA.
13. Mulhearn PJ (1981) Distribution of microbubbles in coastal waters. J Geophys Res 86(C7): 6429-6434.
14. Wienke BR (2016) Biophysics and diving decompression phenomenology. Bentham Science Publishers, Sharjah, UAE.
15. Ostwald W (1897) Studies on the formation and transformation of solid bodies. Z Phys Chem 22: 289-304.
16. Lifshitz IM, Slyozov VV (1961) The kinetics of precipitation from superheated solid solutions. J Phys Chem Solids 19: 34-45.
17. Wagner C (1961) Theory of the aging of envious beating by Umlosen. Electrochemie 95: 581-597.
18. Baldan A (2002) Progress in ostwald ripening theories and their applications to nickel based superalloys. J Mat Sci 37: 2172-2202.
19. Kabalnov AS, Schukin ED (1992) Ostwald ripening theory: Application to fluorocarbon emulsion stability. J Coll Inter Sci 38: 69-97.
20. Del Cima OM, Oliveira PC, Rocha CM, Silva HS, Teixeira NC (2017) Gas diffusion among bubbles and the DCS risk. Fluid Dyn, arXiv:1711.08987v1.
21. Wienke BR, O’Leary TR (2009) Diving decompression models and bubble metrics: Dive computer syntheses. Comp Biol Med 39(4): 309- 311.
22. Wienke BR (2010) Computer validation and statistical correlations of a modern decompression diving algorithm. Comp Biol Med 40(3): 252- 270.
23. Wienke BR (2015) Deep stop model correlations. J BioEng BioMed Sci 5: 12-18.