Investigating a Long-Range Correlation Using Detrended Fluctuation Analysis in Tennis: A Pilot Study

The purpose of this study was to investigate a long-range correlation in elite tennis players’ dynamic behavior during tennis competitions. Fractal dynamics of movement time series in expert tennis players were analyzed using the Detrended Fluctuation Analysis (DFA), which provides the stability of the fluctuations in the time series. Three match videos of elite tennis players (1st round between professionals, the semi-final between top-ranked professionals, and the boys’ final between junior players) were selected and downloaded from the open-source website. Every frame from the high-definition video was captured using Kinovea (sports analysis software), then imported into a custom written MATLAB program that can manually track the displacements of players and tennis balls on the court. Distance time series between player and center mark on the baseline in addition to distance time series between player and tennis ball displacements, were made for each player. The distance time series to the center mark showed that the winner displayed a long-range correlation, αwinner=0.53, whereas the loser had a random correlation, αloser=0.47, in the 1st round. In the boys’ final, the winner had αwinner=0.58 and the loser αloser=0.41. A long-range correlation did not emerge in the semifinal when both players were top ranked players, αwinner =0.45, αloser=0.47. The winner might show greater DFA alpha values than 0.5 as a long-range correlation, indicating the winner maintained a relatively consistent distance from the center of the court during the competition.

Keywords:Performance analysis; Dynamic behavior; Video analysis; Tennis match

Games such as tennis (or table tennis, squash and badminton) consist of two players (dyadic) and the players’ dynamic interaction occurs throughout the game [1,2]. Tennis players repeatedly return to the place near the center mark of the baseline. The relative phase was frequently employed to describe repetitive movement patterns of play between players in tennis [1] as dynamic systems. Players return to the position near the center mark after every stroke [3], usually near the center mark on the baseline, to cover the entire court (maximum coverage). The primary strategy for tennis players is to increase the distance between the ball displacements from the opponent. One player (e.g., receiver) tries to maintain a consistent distance between the receiver and the tennis ball, whereas another player (e.g., attacker) tries to break this consistency. This strategy is a great advantage for making the opponent move around a tennis court left to right (side to side) or close to far from the net (front and back) [4]. More experienced tennis players or winners are expected to demonstrate a stable pattern of staying near the center mark. Due to its unique characteristics, many tennis studies applied the concepts of dynamic systems theory, such as the interdependent, dynamic, and nonlinear complex systems with tennis players as an oscillator and the tennis ball as an attractor [5-7]. The dynamical systems approach is appropriate for revealing the complex behavior of tennis players that are interrelated depending on the tennis ball displacements made by the opponent. This complex relationship was described using the principles of the dynamic system and the use of dynamic systems theory to analyze the behavior of tennis players and their interaction with the ball is a unique and useful approach. The idealized path of lateral distance during a cross rally in tennis is interpreted with a concept of self-organization, showing synchronized behavior [1]. These studies provided an interesting insight into the way in which tennis players behave on the court.

Many researchers were interested in the dynamic behavior of elite tennis players in the time domain [8]. Elite tennis players showed superior performance than amateurs or novice players [5], which can be seen in various fields. The typical approach to revealing the experts’ performance is comparing experts to novices within the Expert Novice paradigm. With high-definition videos these days, the notational analysis was able to analyze dynamic and complex behaviors in tennis, for example, serve and serve return strategies [9,10]. In addition, numerous studies tried to quantify using performance indicators to differentiate the superior performance of experts [4], such as rally length, point profiles and distance covered [11,12]. Martinez-Gallego et al. [12] found the distance as a performance indicator covered by the winner was significantly greater than the loser in tennis. The distance covered by the player can be used as the performance indicator to differentiate experts. Moreover, performance quantification of an expert’s dynamic behavior using the time series may provide additional information, such as the existence of a long-range correlation as a dynamic system. Specifically, detecting long-range correlations as a signature of a dynamic system provides a way to quantify and analyze the complexity of expert athletes’ behaviors. Detrended Fluctuation Analysis (DFA) as a tool to differentiate experts from novices emphasizes the importance of analyzing the structure and patterns in time series data rather than just the raw data itself.

For example, a long-range correlation exists everywhere when investigating nature, traffic flow, quasar emissions, river discharge, DNA base sequence structure, and cellular automata [13,14]. A long-range correlation has been observed in human behaviors such as reaction time, word naming, rhythmic movement timing, rhythmic coordination, repetitive force production, gait, heart rate and neural activity [15]. A long-range correlation is considered as a signature of a dynamic system [3]. In cognitive science, a long-range correlation was discovered in human cognition [13]. However, whether a long-range correlation emerges during sports competition instead of a controlled experiment in the lab is not fully understood. We also examine whether the Detrended Fluctuation Analysis (DFA) can differentiate experts from novices as a performance indicator. There are many statistical procedures to quantify time-series properties, for instance, Hurst exponent, Fourier analysis or Detrended Fluctuation Analysis. DFA is considered a universal statistical property of complex systems [14,16,17] and has been widely used to assess and quantify time series structure [16]. In addition, it is known to be robust and allows us to evaluate fractal dynamics or self-similarity in human behavior [16,18,19]. DFA outcomes are alpha values as a scaling exponent of the time series. If the alpha value is between 0.5 and 1.0, it indicates a persistent time series showing a stable pattern with a long-range correlation. Alpha less than 0.5 means that the time series fluctuates roughly, showing more random and less stable. Kim et al. [3] reported that the time series of ball bounce displacements in a semi-final tennis match did not show a longterm correlation between the top-ranked professional players. Top rankers were skillful at covering the court, and their shots were randomly displaced on the court. It was expected there would be no existence of a long-range correlation between top-ranked players because the goal of tennis is not to be coupled and top-ranked players would perform better following this strategy. There could be another possibility to have unexpected results that a long-term correlation may or may not emerge in the match composed of a top ranker and a lower-ranked player.

The purpose of this study was twofold to investigate the presence of a long-term correlation as a dynamic system showing self-organization in a competition of elite tennis players throughout the match. It will provide meaningful information to process the time series data since previous studies on tennis players’ movements were analyzed in the short term for a single rally or about 30 seconds [2,7]. Furthermore, we examined whether the results of DFA can be a performance indicator that differentiates the level of expertise when comparing a top ranker and a low ranker or between top rankers. First, we assessed tennis players’ dynamic behavior regarding the distance-time series between the player and the tennis ball displacement. Second, we evaluated the dynamic behavior of tennis players as a self-organizing system that tried to stay near the center mark in terms of the distance between the player and the center mark. We hypothesized that the winner would show a long-range correlation between the player and the tennis ball displacement in the distance-time series. Also, we hypothesized the winner would show a long-range correlation in the distance-time series between the player and the center mark.

Matches

Three tennis match videos were selected for a pilot study. First, we chose the 1^st round between one of the top-ranked players (i.e., seeded) and a relatively lower-ranked player (one player completely dominated). The second match was the semi-final between the topranked players (similar level of expertise), and the third was the final of the boys’ singles. These junior players showed outstanding performance as experts but were still amateurs, relatively less skilled than professional players. This research was carried out fully in accordance with the ethical standards of the International Journal of Exercise Science [20].

Protocol

The variables of interest were the distance-time series between a player and the center mark on the baseline and between a player and tennis ball displacements. The high-definition match videos (720p, 25fps) were downloaded from the open-source website, and every frame was captured using Kinovea (www.kinovea.org), a free annotation tool for sports video analysis. Captured frames were imported to a custom-written MATLAB program to track the players’ and tennis ball displacements. Serves were excluded because tennis players were in a set-up position after points. Tennis balls behind the baseline and sidelines were considered out of bounds and these displacements were not included in the time series. This exclusion procedure built a pure distance-time series consisting of players’ movement patterns, and it does not affect DFA alpha even if a small number of points are deleted [21]. Table 1 shows the number of frames and number of strokes made by each player. Also, it shows how many frames were included in the time series after excluding serves and outs. The distance from the tennis ball displacements and the center mark to players was calculated. There were four different distance-time series: 1) between player #1 and tennis ball displacements when player #2 hits, 2) between player #2 and tennis ball displacements when player #1 hits, 3) between player #1 and center mark when player #2 hits, and 4) between player #2 and center mark when player #1 hits. DFA was applied to these time series to quantify the fractal dynamics in the distance-time series.

Table 1:The number of frames from the match. Note: G1: 1^st round, G2: semi-final, G3: boys’ final, p1: player #1, p2: player #2.

Statistical analysis

A Series of independent t-tests were conducted on the mean distances between players and tennis ball displacements and between players and the center mark. The statistical analyses were completed using the SPSS (v24, IBM, NY, USA). A significance level was set at α=0.05. In addition, DFA was used to analyze and quantify the fractal dynamics in the distance time series.

every time series and the outcomes of DFA results are presented in Table 2. In the 1st round, the winner had a mean distance of 465.83 (SD=219.08) between the player and tennis ball displacements, while the loser had a mean distance of 517.11 (SD=247.32). There was a 51.28cm difference, and the t-test result was close to the margin but not significant (p=0.051). Also, no significant difference was found (p=0.706) in the mean distance between the player and the center mark showing 288.16 (SD=174.49) for the winner and 296.08 (SD=200.31) for the loser. The interesting results between the top-ranked and relatively lower-ranked players in the 1st round match are shown in Table 2. DFA alphas for the winner were 0.50 and 0.53 in the distance-time series between the player and tennis ball and between the player and center mark, respectively. In contrast, the loser demonstrated 0.48 and 0.47 of DFA alphas, respectively. In a match between top-ranked players, the winner showed a mean distance of 595.15 (SD=232.60) between the player and the tennis ball displacement and 272.78 (SD=128.49) between the player and the center mark. The loser showed a mean distance of 490.88 (SD=212.06) between the player and the tennis ball displacement and 257.65 (SD=166.31) between the player and the center mark. The loser showed a smaller mean distance and there was a significant difference between the two players in the distance-time series between player and tennis ball displacements (p<0.001). The mean difference in distance between the player and the tennis ball was 104.27cm, which seemed quite far from the tennis ball displacement. Both top-ranked players demonstrated a random correlation with alpha values less than 0.5 in every time series.

Table 2:Normative data and DFA alphas. Note: P1: player #1, P2: player #2, G1: 1st round, G2: semi-final, and G3: boys’ final. Symbol * denotes a significant difference at p<0.05, and symbol ǂ denotes a long-range correlation between 0.5 and 1.0 as α value.

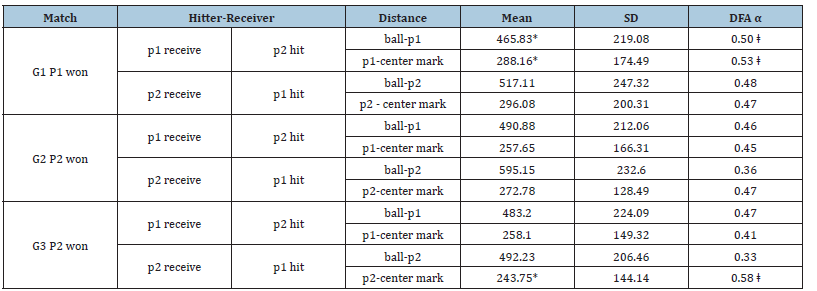
Figure 1 shows an example of the distance-time series from the final of boys’ singles between player and tennis ball and between player and center mark. There is a difference between the winner’s time series on the dotted line and the loser’s time series on the solid line. In boys’ singles, the winner had a mean distance between the player and the tennis ball displacement of 492.23 (SD=206.46) and the loser had a mean distance of 483.20 (SD=224.09). The difference in mean distance was not significant (p=0.677). The winner displayed a mean distance of 243.75 (SD=144.14) to the center mark from the player, whereas the loser showed 258.10 (SD=149.32), not statistically significant (p=0.332). A long-range correlation emerged for the winner (α=0.58) but not for the loser (α=0.41). The DFA alpha value might differentiate the winner from the loser when an expertise level exists. These results may indicate that the winner maintained the distance consistently closer to the ball displacement and center mark when the opponent attacked. Moreover, the winner’s dynamic behavior showed a long-range correlation meaning their distance-time series was more stable and consistent and the fluctuation was less rough than the loser’s.

Figure 1:Solid line represents the time series of the loser and a dotted line represents the winner in the final of the boys’ singles. (a) The distance-time series between the player and the tennis ball displacement in the final of boys’ singles and (b) the distance-time series between the player and the center mark in the final of boys’ singles. (c) DFA results of the players in the final of boys’ singles. The coefficient alpha relating log (Fn) to log (n) is the slope of a least-square line of the integrated time series and detrended time series.

The purpose of the present study was to investigate long-range correlations in the distance-time series of elite tennis players during competition. This study provided preliminary results regarding the mathematical properties of dynamic systems in tennis using Detrended Fluctuation Analysis (DFA). Although we analyzed a small number sample size as a pilot study, the results have significant potential to enhance our understanding of the behavior of expert athletes. As we expected, winners tended to exhibit greater alpha values than losers, indicating less fluctuation in the distance-time series from the center mark. This is partially consistent with our hypothesis, as the results showed a long-range correlation in the athletic behavior of the winner when there is a difference in expertise levels, such as in the 1st round matches or when the players are less experienced experts, such as junior-level players. In previous research, it was found that winners, who are more experienced and skillful players, tend to chase the tennis ball and return to a position near the center mark for positional advantage [5]. Similarly, another research also indicated that the winners in tennis matches tend to cover longer distances than the losers [11] and more advanced players cover significantly greater distances than recreational players [22]. However, we found no significant differences in the mean distance between winners and losers. On the other hand, losers, who are relatively less experienced and skillful players, may have difficulty chasing the tennis ball and returning to a position near the center mark.

In the case of top-ranked players, both winners and losers demonstrated more random fluctuations and might attempt to disrupt stable interactions for positional advantage following tennis strategies. Since both are highly skilled players, their coverage might be more expensive than that of less experienced experts. Winners tend to stay near the center mark to maximize the range of their coverage on the tennis court. We often observe these movement patterns between players whose ranking vary significantly in the tennis game. More skillful players employ diverse shot selections, making the opponent move from side to side and front and back. In Table 2, all winners from 1st round and boys’ final showed a smaller distance from the center mark, indicating that winners tend to stay near the center mark of the baseline [5,1,7], except for semi-final. Consistent with findings in the previous research, DFA revealed no long-range correlations in every distance-time series for top-ranked players. Kim et al. [3] reported that the ball location time series did not show a long-range correlation, which is understandable because the ball displacements should be random for top-ranked players to disrupt stable interactions and win points [8]. Predicting the tennis ball displacements and movements of topranked players in tennis is likely a challenging task compared to lower ranked players. However, it is important to note that we did not consider movement speed in this study as top-ranked players might move faster to track tennis ball displacements made by an opponent and increase the court coverage by quickly coming back to the position near the center mark.

This study has certain limitations that should be considered in future studies. First, we have a small number of sample matches as a pilot study since it examines the possibility of a long-range correlation using DFA as a performance indicator in tennis competitions. Second, the number of shots taken in each game varied and was uncontrollable during a match. Shorter time series could result in smaller DFA values, while longer time series are more likely to exhibit long-term correlations. In conclusion, our study demonstrated that DFA provides a statistical characteristic of a distance-time series throughout an entire match in terms of a long-range correlation. When there is an expertise level difference existed between players, as in the 1st round, the alpha value differentiated the winner from the loser by revealing a long-range correlation. This is attributed to the winner’s ability to maintain a consistent distance from the center mark. DFA may have potential applications as a performance indicator in tennis competitions. Future studies should consider examining a larger number of sample matches across various levels of expertise, including female players.

References