- Submissions

Full Text
Research & Development in Material Science
Josephson Junction, the Quantum Engine: from S.QU.I.D. Sensors to Qubits for Quantum Computers
Eliene B Simão-Silva, Galdino JF, Faddul-Stelzenberger AS, Boareto-Mendes AJ and Fernando M Araujo-Moreira*
Department of Science and Technology, Military Institute of Engineering/IME, Brazil
*Corresponding author:Fernando M Araujo-Moreira, Department of Science and Technology, Military Institute of Engineering/IME, Brazilian Army, Brazil
Submission: May 16, 2023;Published: May 24 2023

ISSN: 2576-8840 Volume 18 Issue 5
Abstract
In this review of our own work, we show the physics and applications of Josephson Junction (JJ) and 2D arrays (JJA) made with this powerful quantum engine. This study is based on more than twenty articles published in more than two decades. In actual days, applications of this device go from the most sensitive sensor to measure magnetic flux, called S.QU.I.D. (from Superconducting Quantum Interference Device) to quantum bits. A unit cell of a JJ, with a cost of about a few hundred dollars allows the availability of a magnetometer with a cost of about one million dollars to a quantum computer with cost of about ten million dollars. The Josephson junction is an old quantum engine for a rising new world with incredible disruptive technological possibilities.
The article is organized as follows: in section 1 we give a short introduction to the subject; section 2 describes the physics of the Josephson effect and the engineering of the Josephson junction; in section 3 we show the magnetic, transport and thermal properties of 2D-JJA; and in section 4 we show the relation between JJA and superconducting granular systems, in particular those related to High-Temperature Superconductors (HTS).
Keywords:Josephson effect; Josephson junction; Josephson junction arrays; Superconducting sensors; Superconducting detectors; Granularity; High temperature superconductivity
Introduction
Never in human history have science and technology affected every aspect of society so much as they do today. In particular, high-tech devices (sensors, detectors, and actuators) are affecting economic growth, development, the security and sovereignty of countries, international relations, and of course, the nature and features of warfare. Because we are immersed in this revolutionary period, called Fourth Industrial Revolution (4th IR) it is hard to have a clear understanding of how deep can be its consequences for humanity
The first Industrial Revolution was initiated in the second half of the eighteenth century and caused profound transformations for humanity through the emergence of industry and capitalism. Since then, the world has changed so much. Human and Nature sciences are comprising studies of natural phenomena, the animal world, and secrets of the functioning and behavior of human beings. Genetic algorithms, artificial neural networks, learning techniques, genetic sequencing, bio printing and drone swarms are some of the lines of research inspired by such studies. However, is Physics that comprises incessant and surprising advances in new materials, nanotechnology, microelectronics and physical infrastructure of Information and Communications Technology (ICT); logic leveraged by Artificial Intelligence (AI), communications protocols and algorithms used in a wide range of applications. Concomitant advances in these dimensions make possible the development of ubiquitous and mobile high-performance internet; smaller, more powerful, and cheaper sensors and detectors; robotics; Internet of Things (IoT), Internet of Things on the Battlefield (IoBT), smart cities, autonomous vehicles, additive printing, wearable technologies, smart weapons, etc. [1].
It is against this backdrop of many disruptive innovations that the Josephson junction - an old quantum engine - resurfaces as one of the most important elements for transforming quantum phenomena into usable technology. This device has important implications for present and future fundamental quantum research and applications such as quantum computing and superconducting single-electron transistor, among others [5].
The Josephson effect and the Josephson junction
Brian Josephson was 22 years old when he did the work - published in 1962 - on quantum tunneling that won him the Nobel Prize in 1973. He discovered that a supercurrent - from superconductor carriers - could tunnel through a thin barrier, predicting, according to physicist Andrew Whitaker, that at a junction of two superconductors, a current will flow even if there is no drop in voltage; that when there is a voltage drop, the current should oscillate at a frequency related to the drop in voltage; and that there is a dependence on any magnetic field. This became known as the Josephson Effect and the junction as a Josephson Junction (JJ). This is a phenomenon that occurs when two superconductors are placed in proximity, with a barrier or restriction between them (called weak links). This effect produces a supercurrent that flows continuously without any voltage applied, across the Josephson junction. The weak link can be a thin insulating barrier (known as a superconductor-insulator-superconductor junction, or S-I-S), a short section of non-superconducting metal (S-N-S), or a physical constriction that weakens the superconductivity at the point of contact (S-c-S) [6,7] as shown in Figure 1; [8]. Types of Josephson junctions include (a) φ Josephson junctions (Josephson junction which has a non-zero Josephson phase φ across it in the ground state); (b) Long Josephson Junction (LJJ, is a Josephson junction which has one or more dimensions longer than the Josephson penetration depth, 𝜆J; however, this definition is not strict); and (c) Superconducting Tunnel Junction (STJ; it consists of two superconductors separated by a very thin layer of insulating material).
Figure 1:Types of weak links: (a) a thin insulating barrier (tunnel junction) that can be superconductor-insulatorsuperconductor junction (S-I-S type), or superconductor-non-superconducting metal-superconductor junction (S-N-S type); (b) microbridge and (c) a physical constriction that weakens the superconductivity at the point of contact [8].

The NIST (National Institute of Standards & Technology) standard for one volt is achieved by using an array of 20,208 Josephson junctions in series. In precision metrology, the Josephson effect provides an exactly reproducible conversion between voltage and frequency. When a high-frequency current is applied to a Josephson junction, the AC Josephson current will synchronize with the applied frequency giving rise to regions of constant voltage in the I x V curve of the device (called Shapiro steps). For voltage standards, these steps occur at the voltages nf/KJ where n is an integer, f is the applied frequency and the Josephson constant KJ=483597.9 GHz/V is a constant equal to 2e/h. These steps provide an exact conversion from frequency to voltage. Because frequency can be measured with very high precision, this effect is used as the basis of the Josephson voltage standard, which implements the international definition of the conventional volt [6].
Figure 2:Sketch of a Superconducting Single-Electron Transistor (SSET); the island is connected to two superconducting electrodes by Josephson junctions biased by a current source (I) where the island can be polarized by a capacitance connected to a voltage source (V) [9].
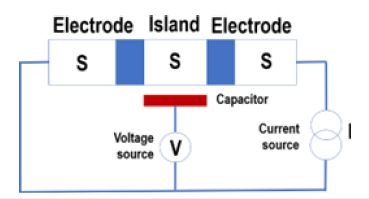
Also, single-electron transistors are often constructed by using superconducting materials, allowing us use to be made of the Josephson effect to achieve novel effects resulting in the socalled superconducting single-electron transistor (SSET, Figure 2; [9]). The Josephson effect is also used for the most precise measurements of elementary charge in terms of the Josephson constant and von Klitzing constant which is related to the quantum Hall effect. Josephson junctions are also used in superconducting quantum computing such as flux qubits or other ways where the phase and charge act as the conjugate variables [6,7].
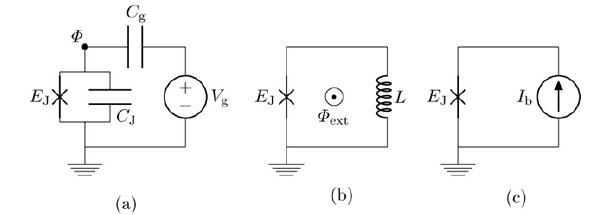
Superconducting quantum computing utilizes STJ-based circuits, including charge, flux, and phase qubits. Also, STJs can be used as direct detectors where the junction is biased with a dc voltage less than the gap voltage. A photon absorbed in the superconductor breaks the superconducting carriers (i.e., the Cooper pairs) and creates quasiparticles. They tunnel across the junction in the direction of the applied voltage, and the resulting tunneling current is proportional to the photon energy. Therefore, STJ can be employed as single-photon detectors for photon frequencies ranging from x-rays to infrared values7The Josephson effect has found wide usage with many practical applications because it exhibits a precise relationship between different physics quantities, such as voltage and frequency, facilitating highly accurate measurements. Josephson junctions have important applications in quantum-mechanical circuits in very sensitive magnetometers like S.QU.I.D. (Superconducting Quantum Interference Device; Figure 3; [10]), superconducting qubits, and RSFQ (Rapid Single Flux Quantum) digital electronic devices that use Josephson junctions to process digital signals [6,7,11,12]. In quantum computing, and more specifically in superconducting quantum computing, the qubit is a superconducting device based on a SIS Josephson junction designed to operate as a quantum bit (Figure 4). There are three basic designs for Josephson-junction qubits, depicted in Figure 4. The three are known as a charge qubit (Figure 4(a)), a flux qubit (Figure 4(b)), and a phase qubit (Figure 4(c)), respectively. The charge qubit is a box for the charge, controlled by an external voltage Vg; the flux qubit is a loop controlled by an external magnetic flux Φext; and the phase qubit is a Josephson junction biased by a current Ib.
Figure 3:Sketch of a Superconducting Quantum Interference Device (S.QU.I.D.) where: A are the Josephson junctions, B is the superconducting ring, and C is the biasing current. The period of the variation of the voltage signal (in red) corresponds to an increase of one quantum of magnetic flux, 𝜙0 [10].
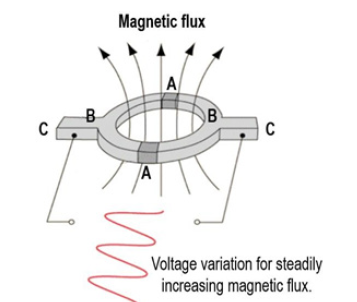
Figure 4:There are three basic designs for Josephson-junction qubits: (a) charge qubit, (b) flux qubit, and (c) phase qubit, where EJ is a Josephson junction with capacitance CJ, Φext is the external magnetic flux and Ib is the bias current [11].
Since the last decades of the twentieth century, Josephson junctions have also been used in large arrays represented by JJA. They have been used to study the physics of low-dimensional systems i.e., solid-state system in which the spatial dimension is less than three like a thin film (2D), a layer (2D), or a wire (1D). These JJA have also proven to be extremely useful model systems for studying a wide variety of other physics, including phase transitions in frustrated and random systems, dynamics in coupled nonlinear systems, and macroscopic quantum effects among others [13,14].
Magnetic, transport and thermal properties of JJA
The large Josephson Junction Arrays (JJA) mentioned at the end of the last section, consist of islands of superconductor, usually arranged on an ordered lattice, coupled by Josephson junctions (Figure 5); [15]. An N x N Josephson junction array is represented by N2 coupled nonlinear differential equations. According to Newrock et al. [13], the response of JJA to various driving currents often aids theoreticians in generating solutions to the equations that often suggest experiments to physicists.
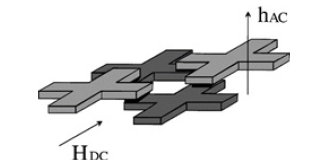
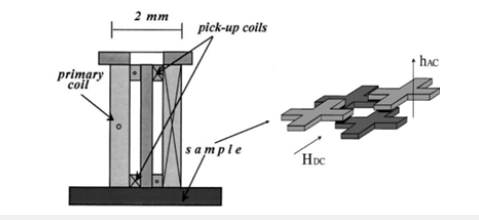
Figure 5:Sketch of a unit cell of the JJA; the crosses are niobium islands, and the junctions are in the overlap region between them. hAC is the oscillating excitation field from the primary coil and HDC is a DC magnetic field, applied in the direction parallel to the sample [15].
Since JJA are artificial, they are very well characterized, leading to an interesting synergy between experiments, computer simulations, and applied mathematics and theoretical physics. The discrete nature of an array and the well-known physics of a Josephson junction allows easy computational simulations of JJA behavior, and their results can be compared to experiments or suggest the need for extra experiments. This is of considerable benefit, for example, in studying high-temperature superconductors since JJA with the disorder can be shown to be the limiting case of an extreme inhomogeneous type-II superconductor, allowing the study of such superconductors in the JJA in which the disorder is nearly exactly known. Because of that, JJA are powerful artificial structures equivalent in many aspects to granular superconducting systems.
In this section, through nine of our own scientific papers, we briefly show our results for the physical properties (magnetic, thermal and transport) of JJA. They were obtained by studying shunted and unshunted SIS and SNS Josephson junctions (Figure 6) formed by 10.000 units of these structures. We have considered the geometrical parameters of those structures [16,17]. Their magnetic properties were determined by using the mutual-inductance technique (Figure 7);[18].
Figure 6:Geometrical characteristics of Josephson junction in JJAs: (a) SIS unshunted junction; (b) SIS shunted; (c) SNS junction. The figure also shows the Nb islands and the shunt resistor [18].
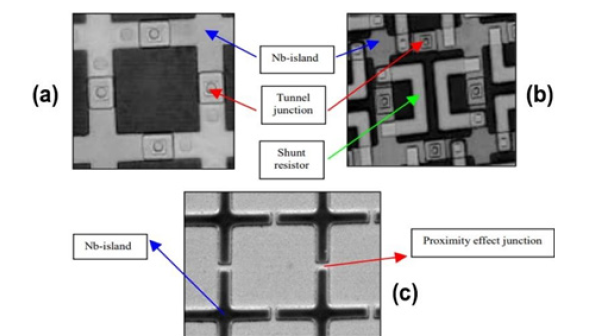
Figure 7:Sketch of the experimental setup for the mutual-inductance technique. The two pickup coils are counter wound [18]. The unit cell of the array (at the right in the figure) is the same shown in Figure 4.
Influence of non-uniform critical current density profile on magnetic field behavior of AC susceptibility in 2D Josephson junction arrays [19]:Employing mutual-inductance measurements (Figure 7), we study the magnetic field dependence of complex AC susceptibility of artificially prepared highly ordered (periodic) two-dimensional Josephson junction arrays of unshunted Nb-AlOx- Nb junctions. In this work we found clear experimental evidence for the influence of the junction non uniformity on magnetic field penetration into the periodic 2D array of unshunted Josephson junctions. By using the well-known AC magnetic susceptibility technique, we have shown that in the mixed-state regime, the AC field behavior of the artificially prepared array is reasonably well fitted by the single-plaquette approximation of the overdamped model of 2D-JJA assuming inhomogeneous (Lorentz-like) critical current distribution within a single junction (Figure 8).
Figure 8:The dependence of the magnetic susceptibilities, 𝜒’(T, hAC) and 𝜒’’(T,hAC), on AC magnetic field amplitude hAC for different temperatures: T=4.2K (a, b), T=6K (c, d), and T=8K (e, f). Solid lines correspond to the fitting of the 2D-JJA model with nonuniform critical current profile for a single junction [19]. The total AC susceptibility is defined as 𝜒=𝜒’+ i𝜒’’.

Manifestation of geometric effects in temperature behavior of AC magnetic response of Josephson junction arrays [20]:By improving the resolution of the homemade mutual-inductance measurement technique, a pronounced steplike structure (with the number of steps n=4 for all AC fields) has been observed in the temperature dependence of AC susceptibility in artificially prepared two-dimensional Josephson junction arrays (2D-JJA) of unshunted Nb-AlOx-Nb junctions with the inductance-related parameter βL(4.2 K)=30. Using a single- plaquette approximation of the overdamped 2D-JJA model, we were able to successfully fit our data assuming that the steps are related to the geometric properties of the plaquette. The number of steps n corresponds to the number of flux quanta that can be screened by the maximum critical current of the junctions. The steps (Figure 9) are predicted to manifest themselves in arrays with the parameter βL(T) matching a “quantization” condition βL(0)=2π(n+1) where n is the number of steps.
Figure 9:(a) Experimental results for temperature dependence of the real part of the AC susceptibility 𝜒’(T,hAC) for different ac field amplitudes hAC=41.0, 59.6, 67.0, 78.2, and 96.7 mOe; (b) theoretically predicted dependence of the normalized susceptibility 𝜒’(T,hAC) (for better visual effect, the curves are normalized and for “quantized” values of βL(0)=2π(n + 1) (from top to bottom): n = 0, 3, and 5 [20].
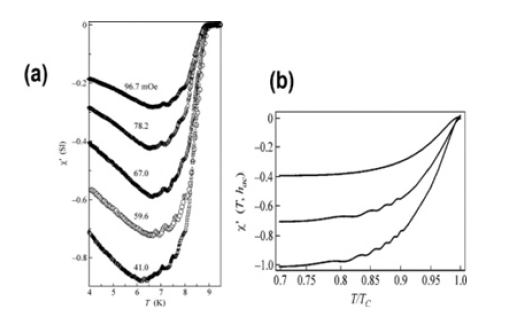
This steplike structure (accompanied by previously seen lowtemperature reentrance phenomenon) was observed for us for the first time in the temperature dependence of AC susceptibility in artificially prepared two-dimensional Josephson junction arrays of unshunted Nb-AlOx-Nb junctions.
Reconstructing 3D profiles of flux distribution in array of unshunted Josephson junctions from 2D scanning S.QU.I.D. microscope images [21]:There are many techniques for imaging sample magnetic fields, including scanning magneto resistive microscopy, magnetic force microscopy, magneto-optical imaging, scanning electron microscopy with polarization analysis, and electron holograph, among others. However, probably one of the most powerful tools for imaging magnetic fields above sample surfaces is the so-called scanning SQUID microscope (SSM) which produces 2D images of the local flux distribution in superconductors, as well as Josephson junctions and its arrays. However, for a better understanding of the underlying mechanisms behind the field penetration, a more realistic 3D visualization would certainly be more helpful. In this regard, it is worth mentioning the attempts to reconstruct 3D images through different techniques based either on numerical simulations or on some kind of pattern recognition algorithm. By using a specially designed algorithm (based on utilizing the so-called Hierarchical Data Format), in this work, we reported the successful reconstruction of 3D profiles of local flux distribution within artificially prepared arrays of unshunted Nb- AlOx-Nb Josephson junctions from 2D surface images obtained via scanning S.QU.I.D. microscope (Figure 10).
Figure 10:(a) 2D SSM image taken from a small section of an JJA at T=4.2K; (b) 3D profile reconstruction from the experimentally obtained for applied magnetic field of 0.5 Oe [21].
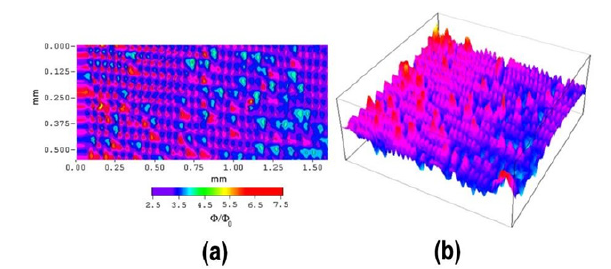
In this work, we demonstrated about the possibility to use 3D image reconstruction technique for better visualization of SQUID microscope surface scans of the local flux distribution within an unshunted array of Nb-AlOx-Nb Josephson junctions. By further improving the resolution of the proposed reconstruction technique (with a necessary modification of the pattern recognition algorithm), it is expected to obtain an important information regarding the formation and evolution of avalanche-like patterns in tunnel (SIS) and proximity (SNS) mediated sandwich structures.
On the field-induced diaelastic effect in a small Josephson contact [22]:Inspired by new possibilities offered by the cuttingedge nanotechnologies, the experimental and theoretical physics of increasingly sophisticated mesoscopic quantum devices heavily based on Josephson Junctions (JJs) and their arrays (JJAs) has become one of the most exciting and rapidly growing areas of modern science. In particular, a remarkable increase of the measurements technique resolution made it possible to experimentally detect such interesting phenomena as flux avalanches, geometric quantization, flux driven oscillations of heat capacity, reentrantlike behavior, manifestation of π-contacts, R-C crossover, unusually strong coherent response, Josephson analog of the fishtail effect, geometric resonance, and field-induced Kosterlitz-Thouless transition, all of them included in this review article. When an elastic solid contains a region with compressibility different from the bulk one, the applied stress induces a spatially inhomogeneous strain field around this region, which results in the softening of its shear modulus C. This phenomenon, known as Diaelastic Effect (DE), usually occurs in materials with pronounced defect structure. By association, Josephson vortices can be considered as defectsrelated inclusions within tunneling contacts. Therefore, one could expect an appearance of magnetic field (H) induced analog of DE in Josephson structures as well. As expected, we have numerically obtained an analog of the diaelastic effect predicted to occur in a small Josephson contact with Josephson vortices manifesting itself as magnetic field-induced softening of the contact shear modulus C(T,H). In addition to Fraunhofer type field oscillations, C(T,H) it was found to exhibit pronounced flux driven temperature oscillations near TC (Figure 11) as predicted [22].
Figure 11:3D flux-temperature profile of the Diaelastic Effect (DE) for different values of the frustration parameter f=H/H0(0), we see characteristic flux driven temperature oscillations of ΔC(T,H) near TC as predicted [22].

Manifestation of geometric resonance in current dependence of AC susceptibility for unshunted array of Nb-Alx- Nb Josephson junctions [23]:Probably one of the most promising tendencies in the modern development of artificially prepared Josephson junction arrays (JJA) is based on the investigation of intricate correlations between their transport and magnetic properties which include, in particular, simultaneous measurements of Current-Voltage Characteristics (CVC) and AC susceptibility. The successful adaptation of the so-called two-coil mutual- inductance technique to impedance measurements in JJA provided a highprecision tool for the investigation of the numerous magnetoinductance related effects in Josephson networks. In this work we presented experimental evidence for the manifestation of novel geometric effects in magnetic response of a high- quality ordered array of unshunted Nb-Alx-Nb junctions under the application of AC current.
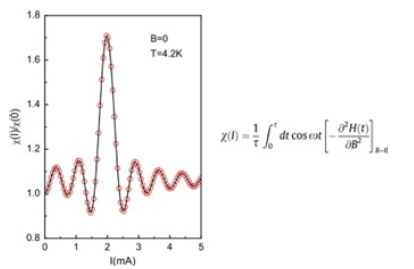
To measure the current induced response of complex AC susceptibility (I) with high precision, we used a homemade susceptometer based on the so-called screening method in the reflection configuration. We observed a characteristic oscillating dependence of the zero-field (B=0) normalized susceptibility (I)/ (0) on applied current I as well as a pronounced resonance-like peak around I=2mA which is clearly seen in Figure 12. We observed that structure in the current dependence of AC susceptibility which was discussed within the single-plaquette approximation. By doing that, we were able to successfully fit our data assuming that resonance structure is related to the geometric (inductive) properties of the array (Figure 12) confirming its origin.
Figure 12:The current dependence of the normalized zero-field susceptibility (I)/𝜒(0) (taken at T=4.2K), along with the best fit (solid line) according to the equation shown the right [23]./p>
Field induced Kosterlitz-Thouless transition in twodimensional array of Nb-AlOx-Nb Josephson junctions [24]:Among many different properties which can be studied using highly ordered two-dimensional (2D) arrays of Josephson Junctions (JJAs) probably one of the most interesting (and important for their potential applications) is their magneto transport behavior, reflecting the evolution of numerous dissipation mechanisms in the arrays under an applied magnetic field. One such mechanism, known as the Kosterlitz-Thouless (KT) topological transition, is related to the creation (and destruction) of bound vortex-anti vortex pairs below (above) some temperature TKT. In zero magnetic field, this transition is expected to manifest itself in 2D systems (including both thin films and JJA) via non-linear current-voltage characteristics (CVC) of the form V∝Ia(T) with power exponent markedly jumping from a=1 at T=TC to a=3 at T=TKT. However, the observation of a rather delicate KT transition in real materials is quite a formidable task because it requires the fulfillment of some strict experimental conditions. Besides, it can be easily masked by other competing mechanisms, such as finite size effects, extrinsic and intrinsic weak links, thermal fluctuations, quasi-particle contributions, etc. On the other hand, KT type transition can be also forced through application of a strong enough magnetic field. In this case, the field induced unbinding of vortex-antiporter pairs takes place near some critical field Hu. The obtained experimental results and their theoretical interpretation suggest a possible manifestation of field induced KT transition in our array seen as a noticeable divergence in the field behavior of the inverse differential magnetoresistance at H=Hu(T)=375 Oe for T=1.7K (Figure 13).
Figure 13:(a) CVC of the array for different temperatures in zero magnetic field; (b) CVC of the array for different magnetic fields at T=1.7K; (c) field dependence of the inverse differential magnetoresistance RN/R(T,H) obtained from the measured CVC and critical current of the array at T=1.7K, along with the best fits (solid lines). Here RN is the normal resistance of the JJA24.
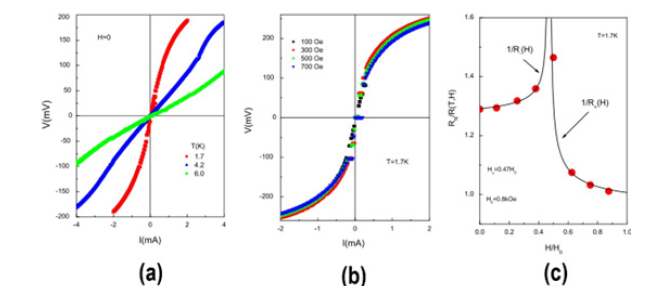
Thus, by measuring current–voltage characteristics of a highly ordered two-dimensional unshunted array of overdamped Nb-AlOx- Nb Josephson junctions in applied magnetic field and by analyzing the resulting differential magnetoresistance, we attributed the observed behavior to the manifestation of field induced Kosterlitz– Thouless transition in our array.
Manifestation of π-contacts in magnetic field dependence of I x V characteristics for proximity- type 2D Josephson junction array [25]:Among many different properties which can be studied using highly ordered 2D arrays of Josephson (or proximity) junctions probably one of the most interesting (and important for their potential applications) is their magneto transport behavior, reflecting an evolution of numerous dissipation mechanisms in the arrays under the applied magnetic field. One of such mechanisms, known as Berezinskii-Kosterlitz-Thouless (BKT) topological transition, is related to the creation (destruction) of bound vortex-antivortex pairs below (above) some temperature TBKT. In a zero magnetic field, this transition is expected to manifest itself in two- dimensional (2D) systems (including thin films and Josephson arrays) via non-linear Current-Voltage Characteristics (CVC) of the form V=RIa(T) with the power exponent a=3 at T=TBKT. However, the observation of a rather delicate BKT transition in real materials is quite a formidable task because it requires the fulfilling of some strict experimental conditions. Besides, it can be easily masked by other competing mechanisms, such as finite size effects, extrinsic and intrinsic weak links, thermal fluctuations, quasiparticle contributions, etc [25].
Results on the temperature and magnetic field dependence of Current-Voltage Characteristics (CVC) were presented for SNS-type 2D ordered array of Nb-Cu0.95Al0.05-Nb junctions (Figure 14). The critical current IC(T,H) and the power exponent a(T,H) are found to have a maximum at the non-zero value of applied magnetic field H/ H0=Hp=225 Oe (Figure 15), which is attributed to manifestation of π-type Josephson contacts in our sample.
Figure 14:SEM photography of high quality ordered SNS type array of Nb-Cu0.95Al0.05-Nb junctions [25].

Figure 15:(a) The evolution of current-voltage characteristics for 2D array of Nb-Cu0.95Al0.05-Nb junctions with applied magnetic field at T=1.7K; (b) magnetic field dependence of the experimental points along with theoretical fits (solidlines) for the critical current IC(T,H) and the power law exponent a(T,H) deduced from the I × V data, taken at T=1.7K [25].

Thus, in this work, by treating the measured current–voltage characteristics for SNS type array of ordered Nb-Cu0.95Al0.05-Nb junctions within standard dissipation scenario, the critical current of the array was found to exhibit a maximum at non-zero value of applied magnetic field which was attributed to the manifestation of π-type contacts in our sample.
Universal resistance capacitance crossover in currentvoltage characteristics for unshunted array of overdamped Nb- AlOx-Nb Josephson junctions [26]:One of the most interesting and important properties of JJA for their potential applications is their transport behavior, reflecting the manifestation of numerous dissipation mechanisms in the arrays via nonlinear Current- Voltage Characteristics (CVC) of the general form V = [I-IC(T)]a(T). It is important to remember that only sufficiently overdamped Josephson junctions with non hysteretic CVC and their arrays can be effectively used in rapid single flux quantum logic circuits and programmable Josephson voltage standards. In this work, we report on our results on CVC for superconductor-insulatorsuperconductor SIS type JJA of strongly overdamped Nb-AlOx-Nb junctions at different temperatures.
The initial CVC data for the array were rescaled by directly introducing the critical current of the single junction IC. Some typical results of the normalized rescaled CVC taken at different temperatures are shown in Figure 16. There, it is interesting to point out that the crossover shows almost a universal behavior taking place around 0.4 for all temperatures. To understand the observed behavior of the CVC in our array, in principle, one would need to analyze in detail the dynamics of the array. However, as we have previously reported because of the well-defined periodic structure of our array, it is reasonable to expect that our experimental results can be quite satisfactorily explained by analyzing the dynamics of a single unit cell of the array.
Figure 16:The normalized rescaled CVC for unshunted array of overdamped Nb-AlOx-Nb Josephson junctions taken at various temperatures along with the best fits. Observe that the value of the crossover shows almost a universal behavior taking place at around 0.4 [26].

It should be noted that we completely ignored inductance geometry-related effects which seem to be of less importance for the interpretation of the observed crossover than dissipation-induced factors resistance and capacitance. However, for a more adequate description of the flux dynamics in truly 2D systems, these effects should be considered. Indeed, as accurate numerical simulations have revealed, both self- inductance and mutual inductance effects will have a significant impact on the array’s dynamic properties through the creation of rather strong self-induced magnetic fields [26].
In this work, we reported on some unusual behavior of the measured Current-Voltage Characteristics (CVC) in artificially prepared two-dimensional unshunted JJA formed by overdamped Nb-AlOx-Nb junctions. The obtained nonlinear CVC was found to exhibit a pronounced (and practically temperature-independent) crossover at some current from a resistance dominated-state below to a capacitance. The origin of the observed behavior is discussed within a single-plaquette approximation assuming the conventional resistively shunted junction model with a finite capacitance and the Ambegaokar-Baratoff relation for the critical current of the single junction.
Thermal expansion of Josephson junctions as an elastic response to an effective stress field [27]:Inspired by possibilities offered by the cutting-edge nanotechnologies, the experimental and theoretical physics of increasingly sophisticated mesoscopic quantum devices heavily based on Josephson junctions and their arrays has become one of the most exciting and rapidly growing areas of modern science. In particular, a remarkable increase in the measurement technique resolution made it possible to experimentally detect many interesting phenomena such as flux avalanches and geometric quantization as well as flux-dominated behavior of heat capacity in Josephson junctions and their arrays, JJA. At the same time, given the rather specific magnetostrictive and piezo magnetic response of Josephson systems, we can expect some nontrivial behavior of the Thermal Expansion (TE) coefficient in Josephson junctions as well. Of special interest are the properties of TE in an applied magnetic field. For example, some superconductors such as Ba1−xKxBiO3, BaPbxBi1−xO3, and La2−xSrxCuO4 were found to exhibit anomalous temperature behavior of both magnetostriction and TE, which were attributed to the field-induced suppression of the super structural ordering in the oxygen sublattices of these systems.
We considered the temperature and magnetic field dependences of the TE coefficient α(T,H) in a small single Josephson junction and in a single plaquette, i.e. a prototype of the simplest JJA. In a short contact, the field-induced α(T,H) is found to exhibit strong temperature oscillations near TC. At the same time, in a JJA (described via a closed loop with finite self-inductance), for these oscillations to manifest themselves, the applied field should be strong enough to overcome the screening-induced self-field effects (Figure 17).
Figure 17:Numerical simulation results for a 5x5 array; the influence of the flux across the void of the network frustrating the whole array on the temperature dependence of the normalized TE coefficients for different values of the barrier [27].
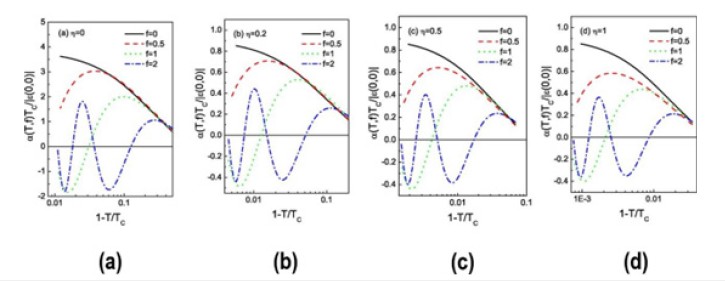
In summary, in this work we have introduced the concept of thermal expansion of a Josephson junction as an elastic response to an effective stress field. We have studied - both analytically and numerically - the temperature and magnetic field dependences of the TE coefficient in a single small junction and in a square JJA. We found that in addition to field oscillations due to Fraunhofer-type dependence of the critical current, of a small single junction also exhibits strong flux driven temperature oscillations near TC. We also numerically simulated the stress-induced response of a closed loop with finite self-inductance (a prototype of an array) and found that α of a 5 × 5 array may still exhibit temperature oscillations provided the applied magnetic field is strong enough to compensate for the screening-induced effects.
Josephson junction arrays and high-temperature superconductors
Persistent shielding currents circulating on superconductors can be detected by magnetization and susceptibility measurements. dc or ac susceptibility may be measured using direct or alternating magnetic fields. These types of measurements have been widely used to accurately determine the critical temperature (TC) of conventional metallic superconductors and, in recent years, to measure the magnetic transition of high-Tc oxide superconductors. In these latter materials, detailed AC susceptibility (𝜒=𝜒’+ i𝜒’’) measurements as a function of temperature and in a fixed AC field amplitude (Hm) typically show two drops in the real component, 𝜒’, and two corresponding peaks in the imaginary component, 𝜒’’, when Hm exceeds some threshold value which depends on sample quality. This suggests a granular behavior such that superconducting regions or grains are coupled through weak links or Josephsontype junctions, reflecting low values of transport critical current densities [28]. On the other hand, AC susceptibility measurements as a function of Hm and in a fixed low temperature typically show two plateaus and two peaks in the real and imaginary parts, respectively. The first plateau at lower Hm values is associated with the total magnetic shielding of the sample. The second plateau is associated with shielding of the grains only, allowing a magnetic field along the grain boundaries, generally a very poor superconducting material. By increasing Hm above the second plateau, exceeding the bulk lower critical field HC1, flux penetrates into the grains (Figure 18); [28].
Figure 18:Data points for both components of the AC susceptibility as a function of the magnetic field amplitude for the YBCO-MTG sample in a fixed temperature. Two plateaus in 𝜒’ and the associated two maxima in 𝜒’’ can be seen at Hm ~ 8.5A/m and Hm ~ 334A/m. Solid lines represent the exponential critical state model fit to the data [28].
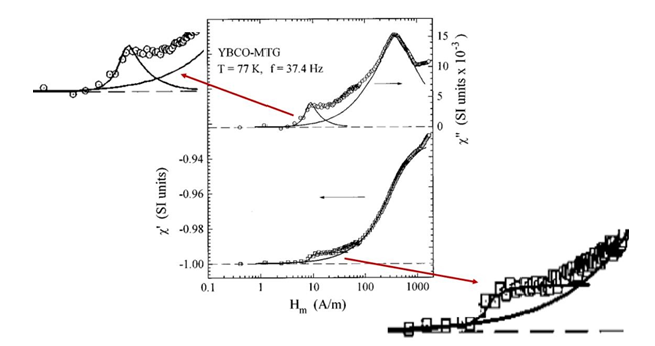
Susceptibility data for polycrystalline samples are complicated to analyze quantitatively. The fraction of intergranular material, the shape, size, and demagnetization factors of the whole sample and grains, the anisotropy of current inside and between grains, the flux pinning properties of granular and intergranular materials, the volume distribution of superconducting parameters, and the coupling properties between grains, are the main factors that influence susceptibility data [28].
In this section, through eight of our own scientific papers, we briefly show our results for granular systems associated to Josephson junction arrays, in particular the problem related to the Paramagnetic Meissner Effect (PME), also called Wohlleben Effect.
Figure 19:Sketch showing equivalent regions between a granular sample and a JJA; (a) typical micrograph of a granular superconductor; (b) A schematic view of a granular superconductor. The grey areas are the superconducting islands separated by white areas of normal material. Josephson contacts are dark rectangles in the connections between the islands; (c) The simplified topology of a regular square unit cell of a JJA.

Granularity in superconductors: intrinsic properties and processing-dependent effects [29]:Granular superconductors can be considered as a collection of superconducting grains embedded in a weakly superconducting (or even non-superconducting) matrix. For this reason, granularity is a term intimately related to High-Temperature Superconductors (HTS). The magnetic and transport properties of these materials are usually manifested by a two-component response. One of them represents the intragranular contribution, associated with the grains which exhibit ordinary superconducting properties. The other component originates from intergranular material, being thus associated with weak-link superconductivity. In this sense, intragranular properties would be inherent, while intergranular, on the contrary, would be extrinsic, generating effects dependent on the processing conditions [29]; Figure 19.
Due to the smallness of the coherence length, practically any imperfection may contribute to both the weak- link properties and the flux pinning in high-temperature superconductors. Such an inevitable dualism brings about a great number of peculiarities and anomalies. Examples of these interesting features (Figure 20) are the Wohlleben Effect (WE) on the field-cooled magnetization (M); the fishtail anomaly on the magnetic field dependence of the isothermal magnetization; the magnetic remanence observed in Josephson Junction Arrays (JJAs); and the occurrence of jumps on the magnetic response of mesoscopic samples submitted to an external magnetic field (H) [29].
Figure 20:(a) Wohlleben effect exhibited by a 3D-JJA of LSCO. The magnetic moment was measured after excitation of the array by an oscillating field h, which is kept off during the DC measurement; (b) Temperature dependence of the magnetic remanence measured for three 3D-JJAs, along with a simulation curve, plotted for the sake of comparison; (c) “Fishtail anomaly” (second magnetization peak) measured for a 3D-JJA of La1.85Sr0.15CuO4. The inset shows the first branch (virgin curve) using a logarithmic scale for the field, so as to emphasize the two peaks exhibited by the magnetization versus field curve; (d) Fishtail anomaly” exhibited by a 3D-JJA of YBa2Cu3O7. The virgin curve is shown at the inset where a logarithmic scale for the field emphasizes the existence of two magnetization peaks [29].

Since some of these anomalies were also observed in macroscopic single crystals and single-domain thin films of both high- and Low-Temperature Superconductors (LTS), one is compelled to consider that there might be at least two levels of granularity in HTS materials. The larger of these two scales would match the typical grain size, being responsible for intergranular effects. The other level, usually called intrinsic, would reside within the grains, being responsible for the inherent magnetic properties of such materials. Although a broad variety of alternative scenarios have been proposed by authors to explain most of these effects, none of them embraces the complete set of oddities. In this work we present a selected set of results (Figure 19) obtained as part of a systematic investigation, evidencing that, in reality, all these effects are distinct manifestations of granularity which, in turn, is envisaged as a break of symmetry [29].
Thermal expansion of granular superconductors based on elastic response of Josephson junction arrays [30]:The effects of penetration of magnetic flux in high-TC superconductors have been the subject of many investigations in the last three decades, especially given their unconventional pairing properties. On the other hand, the important applications for this class of materials strongly depend on their magnetization properties as a critical state is desired to appear at the highest possible fields, which means that the material can support a large supercurrent. Usually, theoretical models for magnetic penetration emphasize some particular properties, such for example as the role of inhomogeneities or defects, multi-connected paths, the presence of unconventional junctions, and surface effects, among others. Special attention has been given to the numerous thermal effects arising from the concurrence between the local temperature oscillations and the presence of defects resulting in the generation of giant flux avalanches. An unusual temperature behavior of the fielddependent thermal expansion coefficient in JJA has been predicted which is based on the elastic response of a Josephson system to an effective stress field. In this work, we analyzed that phenomenon for its potential applications in real materials, using a well-established analogy between JJA and granular superconductors [30].By introducing a concept of Thermal Expansion (TE) of a Josephson junction as an elastic response to an effective stress field (Figure 21), we studied both analytically and numerically the temperature and magnetic field dependences of the TE coefficient in a single small junction and in a square array.
Figure 21:Schematic view of a Josephson contact area in the presence of applied stress and external magnetic field [30].
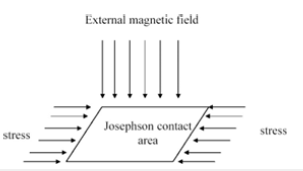
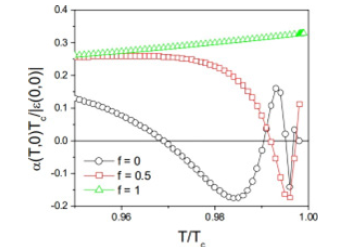
The elastic response of a JJA to a stress field is introduced in order to study the temperature, magnetic field and bias current behavior of the TE of Josephson systems and granular superconductors. The competition between two main contributions (due to stress-induced modification of the inductance parameter) is found to determine the overall TE properties. Since the geometrical inductance is related to the size of the grains (Figure 19(b)), the obtained results are expected to be relevant for the behavior of granular superconductors under stress as well. This is especially true when βL goes to zero, contributing to screening currents relatively strong. In this regime, the difference between arrays and single junctions becomes important. The consequence is that the TE coefficient begins to exhibit flux-driven temperature oscillations close to the transition temperature (Figure 22) just for a relatively large βL. This occurs for a 5x5 JJA. For larger arrays, the same oscillations should be exist at smaller βL values. We observe that during the cooling a negative value of α can induce flux penetration due to the positive strain of JJA [30].
Figure 22:Oscillations of the normalized TE coefficient for an array 5 x 5 for three different values of the magnetic field in the junctions’ loops (f=0, 0.5, 1) which causes the oscillation of the critical current IC with a Fraunhofer-like pattern. The bias and inductance parameter are as follows: Ibias/IC=0.5, βL=20 [30]..
Pinning of spiral fluxons by giant screw dislocations in YBa2Cu3O7–δ single crystals: Josephson analog of the fishtail effect [31]:Probably one of the most intriguing phenomena in the vast area of superconductivity is the so-called Fishtail Effect (FE) which manifests itself as a maximum in the field dependence of the magnetization. There are many different explanations regarding the existence and evolution of FE. However, the most plausible scenario so far is based on the oxygen-deficiency-mediated pinning of Abrikosov vortices in non- stoichiometric materials with the highest possible TC due to a perfect match between a vortex core and a defect size. It has been unambiguously demonstrated that by diminishing the deficiency of oxygen in undoped YBa2COu3O7-δ, the FE decreases and tends to disappear completely. A characteristic field in which this phenomenon usually occurs is of the order of a few Tesla [31].
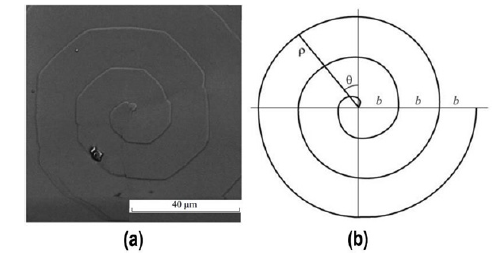
By using the highly sensitive homemade AC magnetic susceptibility technique described in section 3, the magnetic flux penetration has been measured in YBa2Cu3O7–δ single crystals with giant screw dislocations (having the structure of the Archimedean spirals) exhibiting a=3 spiral turnings, the pitch b=18.7μm and the step height c=1.2nm (the last parameter is responsible for the creation of extended weak-link structure around the giant defects). The magnetic field applied parallel to the surface enters winding around the weak- link regions of the screw in the form of the socalled spiral Josephson fluxons characterized by the temperaturedependent pitch bf(T). For a given temperature, a stabilization of the fluxon structure occurs when bf(T) matches b (meaning an optimal pinning by the screw dislocations) and manifests itself as a pronounced low field peak in the dependence of the susceptibility on magnetic field (applied normally to the surface) in the form resembling the high field (Abrikosov) fishtail effect [31]; Figure 23.
Figure 23:(a) SEM photography of YBa2Cu3O7–δ single crystals showing a giant screw dislocation having the structure of the Archimedean spiral, with a=3 spiral turnings and the pitch b=18.7μm (magnification 500×), (b) Sketch of the one-armed Archimedean spiral with three 360° turnings (counterclockwise) in polar coordinates (ρ,θ) and a pitch b defined as the distance between successive turnings [31]..
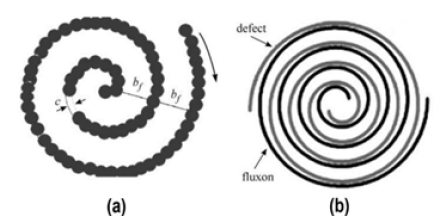
Turning to the discussion of the obtained results, let us show how the formation and pinning (by the Archimedean spirals) of spiral Josephson vortices (fluxons) can manifest itself as a pronounced low-field peak in the measured magnetic response. According to this scenario, the peak field hp(T) (where susceptibility exhibits a fishtail-like low-field maximum) can be related to the fluxon critical field hf(T)=Φ0/dbf. The latter defines the onset for fluxon motion. More precisely, for h0>hf(T) spiral fluxons start to rotate along the weak-link regions of the Archimedean spirals. Here, d=2λL+c~2λL, is the width of the contact with λL, being the London penetration depth of the superconducting region and c the thickness of the non-superconducting region in the vicinity of the screw defined by the vertical step height (distance between terraces of the screw dislocation along the c-axis of YBa2Cu3O7–δ crystal) [31].
Above the critical field of the single spiral fluxon hf(T), the applied magnetic field first starts to penetrate the weakened regions (near the surface of the sample) which are situated in the vicinity of screw dislocations (Figure 24 (a)). There are two possibilities depending on the field orientation. Flux can either enter by climbing up the screw dislocation from bottom to top (for field applied parallel to the surface) or by sliding down the screw from top to bottom (for field applied normally to the surface). In both cases, the freely rotating spiral fluxon eventually gets trapped (stabilized) inside the Archimedean spiral of the defect (Figure 24(b)); [31].
Figure 24:(a) The structure of the one armed Josephson spiral fluxon with pitch bf winding around the Archimedean spiral of the screw dislocation (c is distance between terraces along the c-axis of YBa2Cu3O7-δ crystal). (b) Trapping (stabilization) of the one-armed Josephson spiral fluxon by the matching one-armed Archimedean spiral of the giant screw dislocation [31].
To discuss the temperature evolution of the introduced parameters, in Figure 25(b) we present the fitting results for the temperature dependence of the normalized critical current density JC(T) in our crystals, extracted from the AC susceptibility data using the usual procedure based on the critical state model. A crossover between two different types of behavior is clearly seen near T*=0.8TC. A low-temperature region (T< T*) was found to follow the well-known two-fluid model dependence (solid line in Figure 25(b)) JC(T)= JCT)=>(0)(1-t4)3/2 with t=T/TC, while closer to TC (for T>T*) our data are better fitted by a proximity-type behavior (dotted line in Figure 25(b)) JC(T) = JC(0)(1- t2)2 , most likely related to normal regions produced by oxygen deficiency and defect-related structure.
Figure 25:(a) A fishtail-like structure of magnetic field dependence of the AC susceptibility 𝜒’(T,h0) in YBa2Cu3O7-δ single crystals for various temperatures; (b) the best fits for the dependence of the normalized critical current density on reduced temperature T/TC deduced from the AC susceptibility 𝜒’(T,h0) data [31].
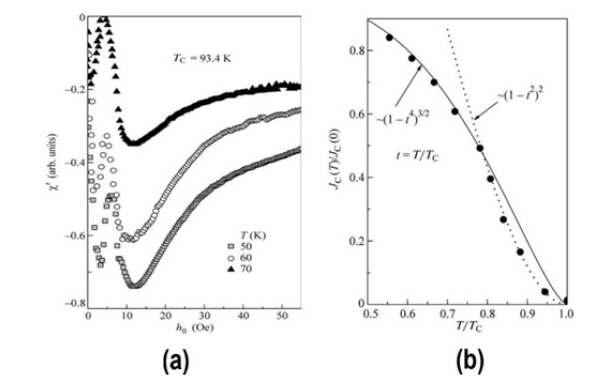
In summary, in this work by employing a highly sensitive home-made AC magnetic susceptibility technique to measure single crystals of YBa2Cu3O7–δ with giant 3D screw dislocations (having the structure of the 2D Archimedean spiral), we observed a manifestation of the low-field analog of the high-field (Abrikosov) fishtail effect, attributed to highly efficient pinning (stabilization) of rotating spiral Josephson vortices by the matching screw defects [31].
Reentrant ac magnetic susceptibility in Josephson-junction arrays: an alternative explanation for the paramagnetic Meissner Effect [15,18]:The so-called Paramagnetic Meissner Effect (PME) was measured in Bi-based high-TC granular superconductors. This experimental study of PME was performed in polycrystalline superconductors and was first reported by Braunisch et al. They measured a paramagnetic dc susceptibility at values of temperature lower than the critical temperature TC of their superconducting samples. This paramagnetic response was in striking contrast to the usual diamagnetic Meissner effect, where the magnetic field is excluded from superconductors. The PME appeared systematically under specific experimental conditions and depended on sample preparation and morphology. It was attributed to the presence of 𝜋 junctions between the grains. In these junctions, the Cooper pair acquires a phase shift 𝜋 across the junction, giving rise to Josephson currents which are negative relative to conventional junctions. Such a phase shift might result from magnetic impurities between the grains or non-s-wave pairing symmetry [15,18].
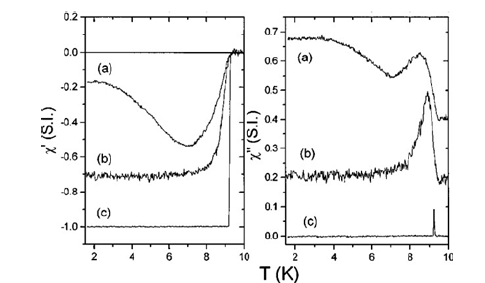
In this research, we reported the appearance of a strong paramagnetic contribution to the complex AC magnetic susceptibility of niobium Josephson junction arrays. Since our arrays are made of conventional junctions, our result shows that PME can occur without the presence of 𝜋 junctions. In our experiment, the paramagnetic contribution appears as a reentrant behavior of the AC susceptibility, 𝜒AC, at low temperatures. The inphase component of the first harmonic, 𝜒’, which is a measure of the screening current, first increases in modulus as the temperature is lowered from the critical temperature TC, then decreases at a lower temperature. The out-of-phase component, 𝜒’’, is correlated with 𝜒’, showing increasing losses as the screening decreases at low temperatures (Figure 26). Moreover, we find that numerical simulations of the simplified case of a four junctions loop exhibit paramagnetic susceptibility in some ranges of excitation field and temperature, accounting very satisfactorily for our experimental results [15,18].
Figure 26:𝜒’ and 𝜒’’ as a function of T for different values of hAC with HDC=0. The curves for 𝜒’’ have been vertically offset for clarity [15,18].
Complex AC magnetic susceptibility is a powerful low field technique that has been successfully used to measure properties such as critical temperature, critical current density, and penetration depth in superconductors. To measure samples in the shape of thin films, the so-called screening method has been developed. It involves the use of primary and secondary coils, with diameters smaller than the dimension of the sample. When these coils are located near the surface of the film, the response, i.e., the complex output voltage V, does not depend on the radius of the film or its properties near the edges. In the reflection technique, an excitation coil (primary) coaxially surrounds a pair of counter wound pickup coils (secondaries). When there is no sample in the system, the net output from these secondary coils is close to zero since the pickup coils are close to identical in shape but are wound in opposite directions. The sample is positioned as close as possible to the set of coils, to maximize the induced signal on the pickup coils [15,18].
In Figure 27 we show results for 𝜒AC(T), obtained from Zero- Field Cooled (ZFC) experiments, for hAC=57 and 96mOe, and with HDC=50. For hAC smaller than about 50mOe, the behavior of both components of 𝜒AC(T) is quite similar to typical superconducting samples. 𝜒’(T), which is a measure of the screening current, becomes more negative at lower temperatures, indicating stronger superconductivity through the Meissner effect. 𝜒’’(T) peaks, indicating a maximum in the losses, around the critical temperature TC. Notice that 𝜒’(T)~-0.7(SI) for hAC=10 mOe, at low temperature. The sample can only partially screen the external magnetic field. As we can see in Figure 27, the screening of the JJA is weaker compared to the screening of a thick ~500-nm niobium film. We, therefore, define the JJA to be in a Meissner-like state for hAC<50 mOe. We qualitatively explain this partial screening through the single-loop picture. Outside the Meissner-like regime, for values of hAC>50 mOe, 𝜒’(T) is reentrant. It first increases in modulus as the temperature is lowered from the critical temperature TC, then decreases at a lower temperature. The minimum in 𝜒’(T) appears at T~7.0K. In all the temperature ranges, at a fixed T the modulus of 𝜒’(T) decreases by increasing hAC. The out-of-phase component, 𝜒’’(T), is correlated with the reentrance observed in 𝜒’(T), showing increasing losses as the screening decreases, indicating an apparent weakening of the order parameter at low temperatures.
Figure 27:𝜒’ and 𝜒’’ from the JJA as a function of T, for (a) hAC=96 mOe, (b) hAC=7 mOe, and (c) from a 500nm thick niobium film for hAC=10 mOe. The curves (a) and (b) for 𝜒’’ have been vertically shifted by 0.2 (SI) for clarity [15,18].

We use a simple multi junction loop model to explain how, in spite of the very different experimental conditions, our experiment can provide an alternative explanation for PME. We have found that all the experimental results can be qualitatively explained by analyzing the dynamics of a single unit cell in the array. The idea to use a single unit cell to qualitatively understand PME was first suggested by Auletta et al. They simulated the field-cooled DC magnetic susceptibility of a single-junction loop and found a paramagnetic signal at low values of the external magnetic field. A later extension of the model to a two- dimensional JJA gave qualitatively the same results. Figure 28 shows these results [15,18].
Figure 28:Simulations of 𝜒’ and 𝜒’’ as a function of T for (a) hAC=5 mOe, (b) hAC=29 mOe, (c) hAC=69 mOe, and hAC=118 mOe. βL(4.2K) = 30 and βC(4.2K)=60. The curves for 𝜒’’(T) have been vertically shifted by 0.4 (SI) for clarity. Clearly, curves (c) and (d) exhibit reentrant behavior in both components [15,18].

Surprisingly, numerical simulations of a very simple model, a four-junctions loop, accounted very satisfactorily for our experimental results, suggesting that this reentrance is dynamic in origin. However, we cannot make a completely quantitative comparison between our model and the measured array. The response of the array results from an average of the response from many loops. The flux distribution in the array is, in general, nonuniform, giving rise to different values of hac in different loops. As a consequence, the measured response of the arrays presents no sharp transitions. The profile of the field penetration in the whole array has been analyzed by other authors but is not included in our model [15,18].
From these experiments and simulations, we conclude that the phenomena causing the reentrance observed in Josephsonjunction arrays should also exist in granular superconductors. We expect these phenomena to appear either as PME, in the case of DC magnetic susceptibility measurements or as an anomalous increase of dissipation at low temperature, in the case of AC magnetic susceptibility measurements [15,18].
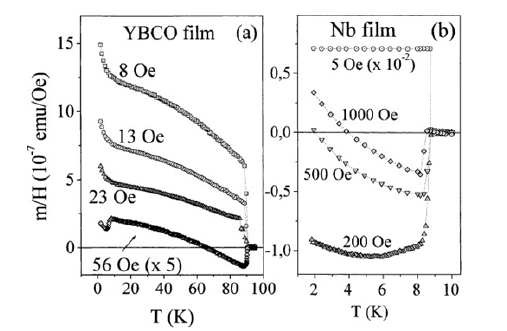
Field-induced networks of weak-links: an experimental demonstration that the paramagnetic Meissner effect is inherent to granularity [32]:In this work, we reported a direct observation that the PME previously described is an inherent consequence of granularity in superconductors. The experiments reported here were performed using high-quality thin films of Nb and YBa2Cu3O7-δ. A network of randomly distributed weak links was induced on the film by the application of a small perpendicular DC magnetic field. The high demagnetization factor arising from this geometry, forces magnetic flux to penetrate into the sample, establishing a pattern of magnetic dendrites. By changing the external field, we can adjust the critical current strength of the weak links, thus controlling the magnetic response of the induced network. In this way, we have tuned the temperature dependence of the field-cooled magnetization. An important conclusion supported by our experiments is that PME results from a competition between positive and negative magnetic responses generated by different levels of granularity in a multigranular system. This is in accordance with previous experiments correlating PME and the dynamic reentrance exhibited by a Josephson junction array, a particularly ordered granular system [32].
In Figure 29 we show the field-cooled runs for Nb and YBa2Cu3O7-δ films. Once again, the observed behavior resembles those previously reported for PME: as the field is increased, the standard response of the Field Cooled (FC) magnetization is reentrant, crossing over from negative to positive values as T is decreased from TC. The fact that we have obtained similar results for high-quality thin films of both high (HTS) and low (LTS) temperature superconductors (YBa2Cu3O7-δ and Nb respectively) corroborated our previous findings about PME [32].
Figure 29:Field Cooled (FC) magnetic susceptibility measured for different values of the applied magnetic field for films of Nb and YBa2Cu3O7-δ; notice the crossover from fully paramagnetic to reentrant as the magnetic field increases [32].
On the origin of reentrance in 2D Josephson junction arrays [33,34]:In this work, we presented a comparative study of the magnetic properties of shunted and unshunted two- dimensional Josephson junction arrays (2D-JJA). Using a single-plaquette approximation of the 2D-JJA model, we were able to successfully fit all our experimental data (for the temperature, AC and DC field dependencies of susceptibility) and demonstrate that the dynamic reentrance of AC susceptibility is directly linked to the value of the Stewart-McCumber parameter βC. Based on extensive numerical simulations, a phase diagram βC-βL is plotted which demarcates the border between the reentrant and non-reentrant behavior in the arrays [33,34].
Figure 30:Numerically obtained phase diagram (taken for T=1K, hAC=70 mOe, and HDC=0) which shows the border between the reentrant (white area) and nonreentrant (shaded area) behavior in the arrays for different values of βL and βC parameters [33,34].
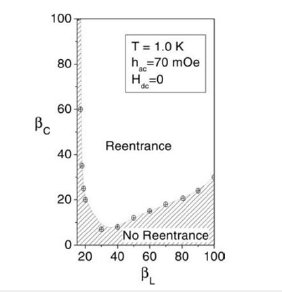
Based on our extensive numerical simulations, a resulting phase diagram βC-βL (taken for T=1K, hAC=70 mOe, and HDC=0) is depicted in Figure 30 which clearly demarcates the border between the reentrant (white area) and non-reentrant (shaded area) behavior in the JJA for different values of βL(T) and βC(T) parameters at a given temperature. In other words, if βL and βC parameters of any realistic array have the values inside the white area, this array will exhibit a reentrant behavior. In addition, this diagram shows that one can prepare a reentrance exhibiting array by changing one of the parameters (usually, it is much easier to change βC by tuning the shunt resistance rather than the geometry-related inductance parameter βL) [33,34].
It is instructive to mention that a hyperbolic-like character of βL vs. βC law observed in Figure 30 is virtually present in the approximate analytical expression for the susceptibility of the plaquette [33,34].
Summary
In this review of our own work covering more than twenty articles and more than two decades of research, we show the physics and applications of Josephson junction (JJ) and 2D arrays (JJA) made with the quantum engine called Josephson junction. It has novel applications going from the most sensitive sensor to measure magnetic flux (S.QU.I.D., Superconducting QUantum Interference Device) to qubits for quantum computers. Here, after a short introduction on the subject, we describe the physics of the Josephson effect and the engineering of the Josephson junction, the magnetic, transport and thermal properties of 2D-JJA as well as the relation between JJA and superconducting granular systems, in particular those related to High- Temperature Superconductors (HTS).
Acknowledgement
We are thankful to all our many colleagues, partners, collaborators, and students who contributed to this work for more two and half decades. We also are gratefully to Brazilian funding agencies FINEP, FAPESP, CNPq and CAPES for financial support.
Conflict of Interest
We declare that do not exist any financial or interest conflicts.
References
- Galdino JF (2023) The importance of integrating the military innovation system and the national innovation system; in: Collection of opinion articles on strategic studies in defense and security. JC Sanches, FM Araujo-Moreira (Eds.), p. 155.
- (2016) Quantum Manifesto - A New Era of Technology.
- Belenchia A, Carlesso M, Bayraktar O, Dequal D, Derkach I, et al. (2022) Quantum physics in space. Physics Reports 951: 1-70.
- Scott EC, Roman AS, Hari PP, Ping L, Madhava S, et al. (2021) Quantum sensing for energy applications: review and perspective. Adv Quantum Technol 4(8): 2100049.
- Wilkinson SA, Cole JH (2019) Linear response theory of Josephson junction arrays in a microwave cavity. Phys Rev B 99: 134502.
- (2016) Reference module in materials science and materials engineering. The Josephson junction - an overview.
- Blamire MG (2021) The potential of the Josephson energy. J Supercond Nov Magn 34: 1629-1632.
- Araujo-Moreira FM (2002) The fascinating world of superconductors. Univerciencia Magazine 2: 39.
- Bouchiat V (1999) Quantum coherence of charge states in the single electron box. Journal of Superconductivity 12(6): 789-797.
- (2023) Home for Physics | Physics (uaf.edu) at Applications (uaf.edu).
- Kockum AF, Nori F (2019) Quantum bits with Josephson junctions. Fundamentals and frontiers of the Josephson Effect; Springer Series in Materials Science, p. 286.
- Huang HL, Wu D, Fan D (2020) Superconducting quantum computing: A review. Sci China Inf Sci 63: 180501.
- Newrock RS, Lobb CJ, Geigenmüller U, Octavio M (2000) The two-dimensional physics of Josephson junction arrays. Solid State Physics 54: 263-512.
- Passos WAC, Araujo-Moreira FM, Ortiz WA (2000) Magnetic remanence of Josephson junction arrays. J Appl Phys 87(9): 5555-5557.
- Araujo-Moreira FM, Barbara P, Cawthorne AB, Lobb CJ (1997) Reentrant ac magnetic susceptibility in josephson-junction arrays. Phys Rev Lett 78: 4625.
- Maluf W, Cecato GM, Barbara P, Lobb CJ, Newrock RS, et al. (2001) Magnetic properties of SIS and SNS Josephson junction arrays. Journal of Magnetism and Magnetic Materials 226: 290-292.
- Maluf W, Araujo-Moreira FM (2002) Controversial features of granular superconductors studied through the magnetic properties of 2D-Josephson junction arrays. Brazilian Journal of Physics 32(3): 717-730.
- Barbara P, Araujo-Moreira FM, Cawthorne AB, Lobb CL (1999) Reentrant ac magnetic susceptibility in Josephson-junction arrays: An alternative explanation for the paramagnetic Meissner effect. Phys Rev B 60(10): 7489-7495.
- Araujo-Moreira FM, Maluf W, Sergeenkov S (2004) Influence of non uniform critical current density profile on magnetic field behavior of AC susceptibility in 2D Josephson junction arrays. Solid State Communications 131: 759-762.
- Sergeenkov S, Araujo-Moreira FM (2004) Manifestation of geometric effects in temperature behavior of AC magnetic response of Josephson junction arrays. JETP Letters 80(9): 580-583.
- Nascimento FM, Sergeenkov S, Araujo-Moreira FM (2012) Reconstructing 3D profiles of flux distribution in array of unshunted Josephson junctions from 2D scanning SQUID microscope images. Physics Letters A 376: 2722-2724.
- Sergeenkov S, Araujo-Moreira FM (2011) On the field-induced diaelastic effect in a small josephson contact. JETP Letters 94(12): 845-848.
- Rivera VAG, Sergeenkov S, Marega E, Araujo-Moreira FM (2010) Manifestation of geometric resonance in current dependence of AC susceptibility for unshunted array of Nb-Alx-Nb Josephson junctions. Physica C 470: 1946-1948.
- Sergeenkov S, Rivera VAG, Marega E, Araujo-Moreira FM (2011) Field induced Kosterlitz-Thouless transition in two-dimensional array of Nb-AlOx-Nb Josephson junctions. Solid State Communications 151: 892-894.
- Rivera VAG, Sergeenkov S, Marega E, Araujo-Moreira FM (2009) Manifestation of π-contacts in magnetic field dependence of I-V characteristics for proximity-type 2D Josephson junction array. Physics Letters A 374(2): 376-379.
- Sergeenkov S, Rivera VAG, Marega E, Araujo-Moreira FM (2010) Universal resistance capacitance crossover in current-voltage characteristics for unshunted array of overdamped Nb-AlOx-Nb Josephson junctions. Journal of Applied Physics 107(9).
- Sergeenkov S, Rotoli G, Filatrella G, Araujo-Moreira FM (2007) Thermal expansion of Josephson junctions as an elastic response to an effective stress field. Physical Review B 75: 014506.
- Araujo-Moreira FM, Ortiz WA, de Lima OF (1996) Exponential critical state model applied to ac susceptibility data for the superconductor YBa2Cu3O7-δ. J Appl Phys 80: 3390-3395.
- Passos WAC, Lisboa-Filho PN, Caparroz R, de Faria CC, Venturini PC, et al. (2001) Granularity in superconductors: intrinsic properties and processing- dependent effects. Physica C: Superconductivity 354(1-4): 189-196.
- Rotoli G, Sergeenkov S, Filatrella G, Araujo-Moreira FM (2008) Thermal expansion of granular superconductors based on elastic response of Josephson junction arrays. Journal of Physics: Conference Series 97: 012235.
- Sergeenkov S, Cichetto L, Rivera VAG, Stari C, Marega E, et al. (2010) Pinning of spiral fluxons by giant screw dislocations in YBa2Cu3O7-δ single crystals: Josephson analog of the fishtail effect. JETP Letters 91(1): 30-34.
- Ortiz WA, Lisboa-Filho PN, Passos WAC, Araujo-Moreira FM (2001) Field-induced networks of weak- links: an experimental demonstration that the paramagnetic Meissner effect is inherent to granularity. Physica C: Superconductivity 361(4): 267-273.
- Araujo-Moreira FM, Maluf W, Sergeenkov S (2005) On the origin of reentrance in 2D Josephson junction arrays. Eur Phys J B 44: 33-39.
- Araujo-Moreira FM, Sergeenkov S (2008) Dynamical reentrance and geometry-imposed quantization effects in Nb-AlOx-Nb Josephson junction arrays. Supercond Sci Technol 21: 045002.
© 2023 Fernando M Araujo-Moreira. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






