Analysis of the Density Dependence of the Grüneisen Parameter for Materials at High Pressures

The Grüneisen parameter γ is of central importance for investing the thermal and elastic properties of materials [1,2]. The Grüneisen parameter is a measure of anharmonicity in the vibrational properties of a crystal. There are two versions of γ, the vibrational Grüneisen parameter γ vibrational and γ thermal [3,4]. The vibrational Grüneisen parameter ,()vibjγfor a particular mode labelled by j is defined as follows [5].

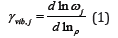
where j_ω is the vibrational frequency of the jth mode and ρ represents density. In the Debye model, the Debye frequency ωD is used in place of ωj, and we have the following relationship from Eq. (1)

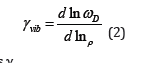
where γ_vib can now be written as γ_D.

The thermal or thermodynamic Grüneisen parameter γ_th is defined as follows [4]

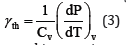
where P and T denote the pressure and temperature, respectively. Cv is the ratio of the constant-volume specific heat to the volume of the material. Roy [6] have performed the vibrational spectrum first-principles electronic structure-based calculations using the Density Functional Theory (DFT) [7] as implemented in the Quantum Expresso package. These ab initio calculations reveal that the Debye frequency has a linear dependence on density to a high level of accuracy. We can write

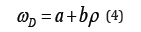
where a and b are material - dependent constants. Using Eqs. (2) and (4) we get

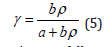
Equation (5) can be rewritten as follows

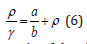
According to Eq. (6), the ratio of density and gamma depends linearly on density. The second order Grüneisen parameter q is defined as [1,2]

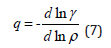
Then, Eqs. (5) and (7) yield

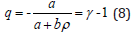
It should be emphasized that at extreme compression, ρ tends to infinity, and therefore, q_∞ tends to zero, and γ_∞ tends to one.

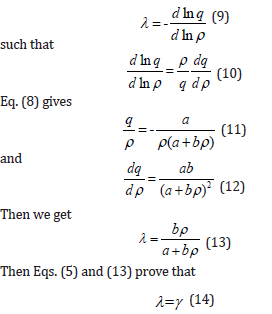
This is an important result according to which the third order Grüneisen parameter is equal to the first order Grüneisen parameter. Thus λ₀=γ₀ and λ_∞ =γ_∞. Eq. (6) at initial or reference values of pressure and temperature gives

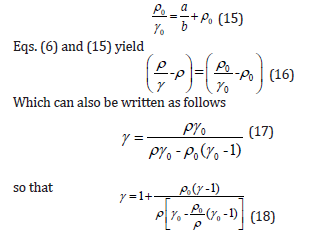
The density ρ tends to infinity in the limit of extreme compression, Eq. (18) givesγ =1_∞ .

Eq. (18) is useful for determining an analytical formula using the Lindemann law [8,9]

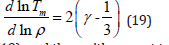
Using Eq. (18) in Eq. (19), and then with respect to density, we obtain

Values of melting temperature at high pressure can be calculated with the help of Eq. (20) provided pressures corresponding to densities are known using an accurate equation of state such as the Stacey reciprocal K-primed equation [10].

The results for γ_∞ , q_∞ and λ_∞ obtained in the present study are consistent with the thermodynamic constraints for solids in the limit of infinite pressure reported by Stacey [2]. According to Stacey we have γ_∞>2/3, q0_∞ → 0, and _λ∞ remains positive and finite. It has been found by Shanker et al. [11] that λ_∞ must be less than K'_∞ , the pressure derivative of bulk modulus in the limit of infinite pressure. The result λ_∞=1 obtained in the present study is consistent with the constraint λ_∞ < K'_∞ because K'_∞ is greater than 5/3 as derived by Stacey [2] on the basis of fundamental thermodynamics of solids.

1. Anderson OL (1995) Equation of state of solids for geophysics and ceramic science. Oxford University Press, New York, USA.
2. Stacey FD, Davis PM (2004) High pressure equations of state with applications to the lower mantle and core. Phys Earth Planet Inter 142(3-4): 137-184.
3. Vocadlo L, Poirer JP, Price GD (2000) Grüneisen parameters and isothermal equations of state. Am Mineral 85(2): 390-395.
4. Anderson OL (2000) The Grüneisen ratio for the last 30 years. Geophys J Int 143(2): 279-294.
5. Ashcroft N, Mermin N (1976) Solid State Physics, HRW International Editions, Holt, Rinchart and Winston.
6. Roy UC, Sarkar SK (2021) Ab initio study of the density dependence of the Grϋneisen parameter at pressures up to 360 GPa. Comput Condens Matter 27: e00552.
7. Martin RM (2004) Electronic structure, basic theory and practical methods. Cambridge University Press, Cambridge, UK.
8. Lindemann FA (1910) Phys Z 11:
9. Gilvarry JJ (1956) The Lindemann and Grüneisen Laws. Phys Rev 102:
10. Stacey FD (2000) The K‐primed approach to high‐pressure equations of state. Geophysics J Int 143(3): 621-628.
11. Shanker J, Sunil K, Sharma BS (2017) The Grüneisen parameter and its higher order derivatives for the Earth lower mantle and core. Physics of the Earth and Planetary Interiors 262: 41-47.