Uncertainty Classification and Modelling

Purpose of designing a system is to manufacture the real system. Mathematical Mechanical Modeling (MMM) process designed for predicting the responses of the real system in its surrounding. Variations in responses are observed due to fluctuations in manufacturing process and configuration associated with the design system. MMM process of the design system, has parameters which can be uncertain. Uncertain parameters result in computational model uncertainties. Decision based on predictions from MMM process design should consider computational model uncertainties and model uncertainties. Uncertainty is a powerful aspect of simulations and highlighting it, directly increases the significance of a simulation [1]. Uncertainties in system at component level propagated to quantify level of reliability. Therefore, to identify all the uncertainties and treat them effectively to solve reliabilities in research studies and decision-making problems.

A systematic uncertainty analysis consists of the following discrete assessments:
(1) Identification, evaluation and tabulation of contributors to uncertainty and their relative influences (sensitivity analysis).
(2) Synthesis of primitive uncertainties to yield the corresponding uncertainty in the characteristic(s) of interest.
(3) Implementation of methods and procedures for minimizing the effects of the primitive uncertainties, when possible.

Not all forms of uncertainty can be predicted or corrected for, but it is reasonable to expect that situations like having fail would not bring the system to a halt [2]. E.g. Uncertainty in measurement can be analyzed with a denser sampling pattern to ensure a reliable assessment [3]. To come with the solutions for the challenges, the manufacturing industries should select appropriate manufacturing strategies, product designs, manufacturing processes, work piece, and tool materials, machinery, and equipment, and so on. The selection decisions are complex due to uncertainties in decision making problems. Decision makers in the manufacturing sector frequently face the problem of assessing wide range of alternative options and selecting one based on a set of conflicting criteria. There are several types of uncertainties which arises in complex engineering design due to source of origin, it is very important to understand classification of uncertainties based on the source of origin.

Classification of uncertainty

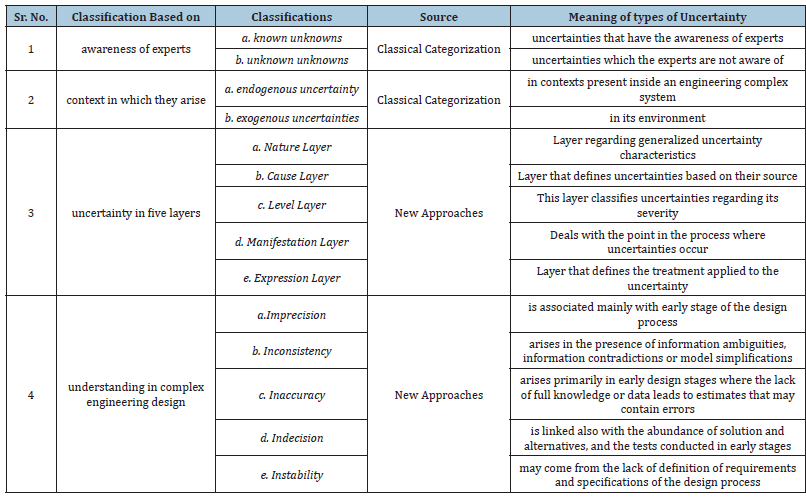
Uncertainty is classified in a broad way as shown in Table 1, it classified based on awareness of experts and context in which they arise classically. Further classified layer by layer uncertainties which exists with various types of occurrences and classified uncertainty based on understanding in complex engineering design.

Table 1: Classification of uncertainty.

Types of uncertainty Vs mathematical theories and methodologies

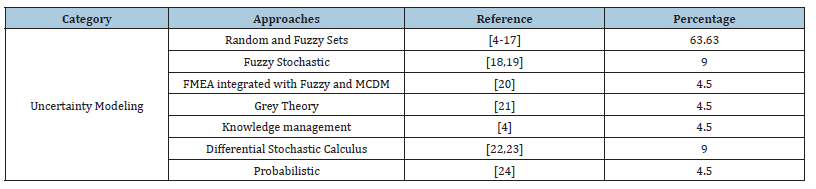
There are certain approaches to deal with uncertainty modeling, Table 2 shown above represents uncertainty modeling approaches and contribution of various researchers [4-24]. It shows that random and fuzzy set approach is widely used for uncertainty modeling. Uncertainty problem can be solved by using FMCDM methods, for user preferred channel [25]. Fuzzy based uncertainty modeling is based on notion of belonging as it is depend on membership function, while use of probability distribution is based on frequency of occurrence [26].

Table 2: Uncertainty modeling approaches used by researchers.

Detailed study of research papers on uncertainty modeling in Mathematical Mechanical Modeling (MMM) shows that researchers are inclined towards fuzzy sets utilization in their research. It was found that 63.63% of researcher from the paper studied shows application of fuzzy sets in uncertainty modeling, further researchers are finding different fuzzy techniques for uncertainty modeling to deal with uncertainty exactly.

1. Ruediger P, Hagen H (2018) Dealing with uncertainties in manufacturing process simulations.
2. Aytug H, Lawley MA, McKay K, Mohan S, Uzsoy R, et al. (2005) Executing production schedules in the face of uncertainties : A review and some future directions. European Journal of Operational Research 161(1): 86-110.
3. Edgeworth R, Wilhelm RG (1999) Interaction with sampling period.
4. Tseng M (2011) Using a hybrid MCDM model to evaluate firm environmental knowledge management in uncertainty. Applied Soft Computing 11(1): 1340-1352.
5. Sanayei A, Mousavi SF, Yazdankhah A (2010) Group decision making process for supplier selection with VIKOR under fuzzy environment. Expert Systems with Applications 37(1): 24-30.
6. Hsu H, Chen C (1996) Aggregation of fuzzy opinions under group decision making. Fuzzy Sets and Systems 79(3): 279-285.
7. Hatami-marbini A, Hatami-marbini A, Tavana M (2010) An extension of the electre i method for group decision-making under a fuzzy environment an extension of the electre I method for group decision-making under a fuzzy environment. Omega 39(4): 373-386.
8. Azadegan A, Porobic L, Ghazinoory S, Samouei P, Kheirkhah AS, et al. (2011) Fuzzy logic in manufacturing : A review of literature and a specialized application. Intern Journal of Production Economics 132(2): 258-270.
9. Kahraman C, Ruan D (2003) Fuzzy group decision making for selection among computer integrated manufacturing systems. Computers in Industry 51(1): 13-29.
10. Castro DM, Parreiras FS (2018) A review on multi-criteria decision-making for energy efficiency in automotive engineering. Applied Computing and Informatics 17(1): 53-78.
11. Krohling RA, Souza TTM De (2012) Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Systems with Applications 39(13): 11487-11493.
12. Deng Y, Chan FTS (2011) A new fuzzy dempster MCDM method and its application in supplier selection. Expert Systems with Applications 38(8): 9854-9861.
13. Haleh H, Hamidi A (2011) A fuzzy MCDM model for allocating orders to suppliers in a supply chain under uncertainty over a multi-period time horizon. Expert Systems with Applications 38(8): 9076-9083.
14. Kaya T, Kahraman C (2011) Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Systems with Applications 38(6): 6577-6585.
15. Kang B, Wei D, Li Y, Deng Y (2017) Decision making using Z-numbers under uncertain. Journal of Computational Information Systems 8(7): 2807-2814.
16. Suo MQ, Li YP, Huang GH (2012) Multicriteria decision making under uncertainty : An advanced ordered weighted averaging operator for planning electric power systems. Engineering Applications of Artificial Intelligence 25(1): 72-81.
17. Zarghami M, Szidarovszky F (2009) Revising the OWA operator for multi criteria decision making problems under uncertainty. European Journal of Operational Research 198(1): 259-265.
18. Zarghami M, Szidarovszky F (2008) A fuzzy-stochastic OWA model for robust multi-criteria. Fuzzy Optimization and Decision Making 7: 1-15.
19. Pishvaee MS, Torabi SA (2010) A possibilistic programming approach for closed-loop supply chain network design under uncertainty. Fuzzy Sets and Systems 161(20): 2668-2683.
20. Liu CH, You JX, Li P, Su Q (2016) Failure mode and effect analysis under uncertainty: An integrated multiple criteria decision. pp.1-13.
21. Dhal PR, Datta S, Mahapatra SS (2011) Flexible manufacturing system selection based on grey relation under uncertainty. International Journal of Services and Operations Management 8(4): 516-534.
22. Booth AT, Choudhary R (2013) Decision making under uncertainty in the retrofit analysis of the UK housing stock : Implications for the green deal. Energy & Buildings 64: 292-308.
23. Hopfe CJ, Augenbroe GLM, Hensen JLM (2013) Multi-criteria decision making under uncertainty in building performance assessment. Building and Environment 69: 81-90.
24. Hodgett RE, Siraj S (2019) SURE : A method for decision-making under uncertainty. Expert Systems with Applications 115: 684-694.
25. Aruldoss M, Lakshmi TM, Venkatesan VP (2013) A survey on multi criteria decision making methods and its applications. American Journal of Information Systems 1(1): 31-43.
26. Herroelen W, Leus R (2005) Project scheduling under uncertainty : Survey and research potentials. European Journal of Operational Research 165(2): 289-306.