Modeling the Wax Deposition Process and Diffusion Kinetics of Wax Crystallization

Due to the depletion of reserves of medium and light oils, the oil, and gas industry has to pay more and more attention to the industrial development of heavy, highly viscous hard-to-recover oil deposits. In the world, light oils are extracted no more than 50%, heavy high-viscosity oils in the range from 10 to 30%, depending on the characteristics of the oil [1] and every year the share of production of heavy oils enriched with high-melting paraffinic hydrocarbons and Resinous-Asphaltene Substances (RAS) increases. In the production of high-viscosity oils, especially in cold climates, serious problems arise associated with the deposition of wax, which reduces the efficiency of field development. Oil is subdivided into low paraffinic (less than 1.5% by weight), paraffinic (from 1.5 to 6%), high paraffinic (more than 6%). This is an important characteristic influencing the technologies used in oil production. Paraffinic oils have the ability to form deposits on the walls of the well, as a result of which there is a decrease in debt and, in the future, blockage of the well. The practice of oil production in the fields shows that the main areas of accumulation of Asphaltene-Resin-Paraffin Deposits (ARPD) are well pumps, lifting strings in wells, flow lines from wells, reservoirs of field gathering points [2].
In practice, two methods are used for calculating the crystallization of ARPD, on the basis of which there is: the diffusion mechanism [3] and crystallization from a supersaturated solution. The diffusion mechanism is based on a three-stage scheme: 1. paraffin begins to crystallize, forming a crystal core when the temperature is below WAT 2. crystal growth and 3. deposition on a cooled wall, the driving force is - the temperature difference between the equipment wall and fluid flow [4]. This mechanism is often used for calculations in the tubing and underground equipment.
With the crystallization mechanism from a supersaturated solution, which is based on the theory of thermodynamic equilibrium of phases, the driving force is the solution saturation. It is assumed that there is a local thermodynamic equilibrium of the phases, the equilibrium in the phases is established instantly and the effect of the diffusion component is determined by the Schmidt number (For oil, Sc> 1000). Often there are assumptions in this mechanism: paraffin crystals are not transferred in a pore medium. If the concentration gradient is not taken into account, then there is no need to consider the process of formation of supramolecular structures. This process should be taken into account in tasks related to pipe transport and waxing of field equipment.
The wax deposition occurs when the oil temperature is lower than the Wax Appearance Temperature (WAT), and there is a temperature gradient between the crude oil and the colder deposition surface. The wax deposition is a function of various factors including flow rate, oil and surface temperature, composition, thermal history, pressure, etc.
The main factor affecting the intensity of the paraffins crystallization is a decrease in temperature, which, in turn, is determined by the degassing process (heat absorption due to degassing and a decrease in temperature due to the Joule-Thomson effect). Thus, the main “driving effect” of reducing well productivity is the degassing process [5].
It is known that the dissolving capacity of oil in relation to paraffins decreases with decreasing temperature and degassing of oil. In this case, the temperature factor prevails [2]. The rate of heat transfer depends on the temperature difference between the fluid and the surrounding rocks at a certain depth, and the thermal conductivity of the annular space between the lifting pipes and the production column.
With an increase in the rate of oil movement, the intensity of deposits initially increases, which is explained by an increase in flow turbulence and, consequently, an increase in the frequency of formation and separation of bubbles from the pipe surface, floating suspended particles of paraffin and asphalt-resinous substances [2]. In addition, the fluid stream tears off part of the deposits from the pipe walls, which can explain the sharp decrease in deposits in the interval 0-50m from the wellhead. The fluid stream, having high flow velocities is more resistant to cooling, which also slows down the formation of ARPD.
The pipe wall roughness and the presence of solid impurities in the system also contribute to the release of paraffin from oil into the solid phase [2]. In addition to these main factors, the intensity of waxing of pipelines during the transportation of water cuttings of good production can be influenced by the water cut of the product [6] and the pH value of formation waters [2].
Studies [4,7] have shown that the most probable mechanism of paraffin formation is the crystallization mechanism, i.e., in conditions when the gas-liquid flow can transport heavy components, the formation, and further build-up of paraffin deposits occur due to the growth of crystals directly on the surface of underground equipment. Wax formation begins where oil comes in contact with the cold walls of underground equipment.

The necessary conditions for the formation of paraffin deposits are [8]:

A. the presence of high-molecular hydrocarbon compounds in oil-primarily paraffins.
B. reduction of reservoir pressure to bubble point pressure.
C. decrease in the flow temperature to values at which the solid phase is separated from oil.
D. the presence of a substrate with a low temperature, on which high-molecular hydrocarbons crystallize with sufficiently strong adhesion to the surface, excluding the possibility of tearing off the deposits by the flow of a gas-liquid mixture or oil at a given technological mode.

There are many other factors that contribute to or prevent the intensive formation of paraffin deposits. The most significant of them can be attributed to the oil flow rate, the process of gas release when the pressure in the pipeline decreases, the presence of mechanical impurities, which are active crystallization centers, the condition of the equipment surface, the water cut of the well production, etc. Various experimental techniques such as flow profile, cold finger and rotating cylinder is used to study the wax deposition phenomenon [9].

Approaches to mathematical modeling and mechanisms of the wax deposition process

The mathematical modeling approach is widely used to predict and monitor wax deposition, either directly numerically or using software that has an internal mathematical model. Wax deposition models are designed based on assumptions and options.
Four wax deposition mechanisms need to be considered when modeling wax deposition growth in pipelines, namely molecular diffusion, shear dispersion, gravity deposition, and Brownian diffusion [10]. Molecular diffusion, which can be described as mass transfer and energy balance, is universally recognized as dominant. At the same time other mentioned mechanisms have been identified as having little impact on this phenomenon.
Some researchers have proposed a shear dispersion mechanism to analyze the wax deposition behavior, especially in laminar flow. However, other researchers reported based on several experiments that this mechanism plays an insignificant role in the deposition of wax [11]. The gravity settling mechanism assumes that wax crystals will settle to the bottom of pipelines because the crystals are denser than oil. However, this effect appears insignificant since experimental studies comparing vertical and horizontal liquid flows did not reveal differences in the amount of deposited wax [12]. Once the wax crystals are deposited and suspended in the oil, the wax crystals will behave according to the Brownian motion rules. Since the effect of motion is likely to transport crystals to areas of lower wax concentration, this can influence the wax deposition behavior. However, its effect is generally considered minimal and is usually neglected during modeling of the overall deposition mechanism. Consequently, the last three mechanisms are not widely accepted, especially for computer simulation procedures [13-15].
Various studies have shown that molecular diffusion is considered the dominant mechanism in the wax deposition process [16,17], and shear stress is significant only when the oil temperature is much lower than WAT and the wax concentration in the oil is high [18].
In turn, the process of wax deposition due to molecular diffusion can be divided into the following five stages [19]:
a. precipitation of dissolved paraffin molecules and formation of a layer of deposits on the surface of the pipe wall.
b. formation of radial gradient concentration of dissolved paraffin components, which leads to the diffusion of paraffin molecules from the bulk of oil to the wall.
c. the deposition of paraffin components on the surface of the existing sediment, which helps to increase its thickness.
d. internal diffusion of paraffin molecules inside the sediment, which leads to an increase in the proportion of solid paraffin in the sediment.
e. counter diffusion of dewaxed oil from the deposit.

Wax deposition modeling software

Table 1:

Various commercial instruments have been developed predict correctly and describe the wax deposition phenomenon [13,20-26]. All wax deposition models follow the same formula for estimating wax deposition thickness. What changes in each model is the calculation of the parameters, which depends on the experimental data. A brief description of the model used by the software is shown in table 1.

Diffusion kinetics of paraffin crystallization

Wax crystallization begins with nucleation, where in oil, solid asphaltene particles with a size of 1nm or a solid phase can be used as nuclei. In [27], an empirical model is used to describe the processes of crystallization and wax deposition, in contrast to which a diffusion model corresponding to the diffusion kinetics of the formation and deposition of waxes from oil is proposed below. The crystallization process is a diffusion process, and the condition is satisfied on the surface of the nuclei [28]

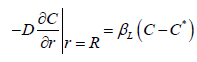
Assuming that dr =Vdt the equation equation of kinetics crystallization of paraffins can be represented as

Here K_p =Vβ_L/ D is the crystallization rate constant, which also depends on temperature T, C-is the concentration of paraffin in the volume of the boundary layer, C∗-is the equilibrium concentration of paraffin in the liquid and solid phases, depending on temperature, β_L -is the mass transfer coefficient, D-is coefficient of molecular diffusion . The solution to this equation can be represented as

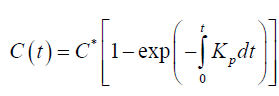
Practical calculations show that this equation can be written in the form

C(t ) = C* (T ) [1− exp(−βtⁿ)] (4)

As follows from equation (4), at t →∞ , we have, C(t) → C∞, where C∞ is the

limiting the concentration of paraffins on the surface of the layer, corresponding to equilibrium and the maximum thickness of the layer of paraffins on the surface.

Figure 1: Crystallization of paraffins from oil at temperatures equal to: 1-370C; 2-270C.

If the maximum thickness of the deposited paraffin layer is equal to the pipe radius, then there is a complete blockage of the pipe section. Using the experimental data [27], it is possible to estimate the coefficients entering the equation (4) as follows β = 0.05, C* (ΔT ) =1.2×10⁹ exp(−7473.5 ΔT ) (where Δ T is the absolute temperature difference between the surface temperature and the crystallization temperature). Practical calculations show that in the indicated limit of temperature change, the exponent changes insignificantly n = 0.65 . The results of experimental studies [27] and calculated values by formula (4) for different temperatures are shown in Figure 1. As follows from Figure 1, the concentration of paraffins eventually tends to the established state.

Model for the formatıon of a dense layer of partıcles on a surface

The formation of a dense layer of paraffin particles on the pipe surface is determined by their transfer to the surface and the nature of the surface itself (roughness). The layer of particles is compacted under the influence of external stresses (pressure) and coagulation phenomena.
The mass of the deposited layer of paraffins on the surface of the cylindrical pipe is determined based on their geometric considerations in the form

m =π ρ_s( R₀² −( R₀ −δ_s)² L =πρ_s (R₀δ_s −δ_s²) L (5 )

In the following description, the index s will apply to all parameters of the deposited layer of paraffin particles. R0-is the radius of the clean pipe (no deposits), δ_s -is thickness of the deposited paraffin layer, ρ_s -is layer density, and L-is pipe length.
Using the expression (5), the change in mass of the deposited layer of paraffins is defined as

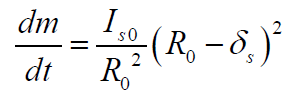(6)

where I_s0 is a diffusion flow of paraffin particles to the clean surface of the pipe. Differentiating (5) determine the change in thickness of the deposited layer in the form

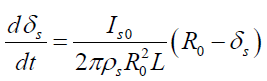(7)

The solution of (7) under the initial conditions (for a clean pipe) is defined in the form

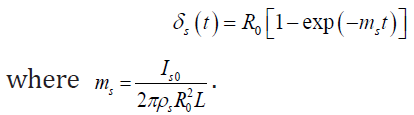(8)

Unlike paraffin particles that form in the volume of the boundary layer, asphalt-resinous substances are contained in oil in a free state. Experimental studies of the sedimentation of asphaltresinous substances [29] in the tubes of heat exchangers showed that the thickness of the deposits can be described by expression (8), with the replacement R for the steady-state value of the thickness δ_m of the deposits, which depends on the flow rate, i.e.

δ_s (t) =δ_m[1−exp(−m_s t)] (9)

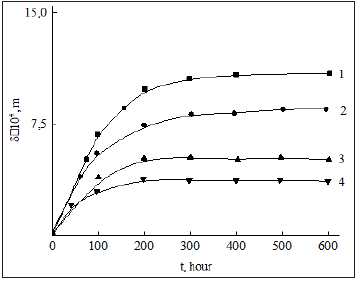
Figure 2 shows the time dependence of the thickness of the deposits at different flow rates. Experimental studies have shown that the limiting value of the deposit thickness depends on the temperature and flow rate [30]. For two temperatures T = 530C and T =1060C , using experimental data, you can write an empirical formula for the limiting thickness in the form δ_m =0.011(T²/V)^6/7.

The relaxation time of particle deposition is approximately equal τ_p= m_s^-1= ( b_m V_k ) ≈ 40 − 65c. Here b_m and k are empirical constants determined from experimental data.

As shown in figure 2, with an increase in the flow rate, the limiting thickness of the deposits decreases, and with an increase in temperature, it increases.

Figure 2: Change in the thickness of asphaltresinous substances on the surface of the pipe from time to time at different flow rates ; 1-0,5m/s; 2-1,0m/s; 3-2m/s; 4-3m/s.

Temperature profile in deposited pipe

The deposition of paraffin particles and asphalt-resinous substances with low coefficient of thermal conductivity contributes to reduce of the oil flow temperature over time with increasing thickness, which has a positive effect on the rate of wax crystallization. Since the formation and deposition process is slow, heat transfer in the deposited pipe can be described by the following equation:

(10)

where is a_T = λ/ (c_ρp_s ) the thermal diffusivity, T_θ is the flow temperature on the outer surface of the pipe, k_R = k_T F/ ( c_ρp_sυ) is the coefficient depending on the heat transfer coefficient k_T, the inner surface of the pipe F and V the volume of the pipe. Determination of this coefficient associated with its dependence on temperature, deposits thickness and time is a composite function.Introducing the following quantities 0 = T −T_θ and τ = r /V transform (10) to the form

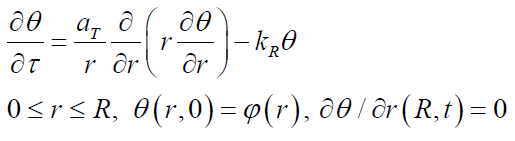(11)

where is ϕ (r) the initial temperature distribution over the pipe section, depending on the initial temperature of the flow in the pipe. Using the method of separation of variables, solution (18) can be represented as

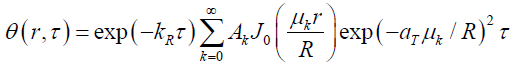(12)

Here J₀ (r) is the zero-order Bessel function of the real argument, A_k, μ_k series coefficients and eigenvalues determined from the boundary conditions and orthogonality conditions of the Bessel functions in the form

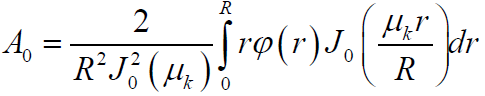(12)

The eigenvalues are determined from the condition J'₀( μ_k) =0, which corresponds to the following values: μ₁ = 0; μ₂ = 3.832; μ₃ = 7.016; μ₄ =10.173...... Thus, the series (19) quickly converges and it is enough to limit itself to the first term, i.e. the temperature distribution in the pipe with deposition can be represented as

(13)

In [30], of flow temperature change with paraffin deposition are given. Since we are limited only to the first member of the series, J₀ (0 ) =1, μ₀ =0 , ϕ (r) = T₀ −T_c, then expressions (13) are simplified to the form.

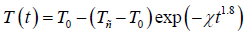(14)

Where χ = 0.875×10⁻¹⁰δ_s/R, T_c is the oil flow temperature in the pipe. Figure 3 shows the temperature distribution in the pipe for different deposit thicknesses.

Figure 3: Distribution of flow temperature in the oil pipeline at various thicknesses of deposits: 1-=20mm, 2-30mm.

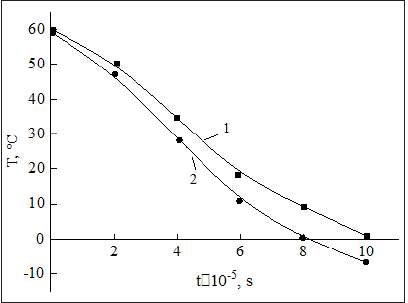
Equation (13) allows to determine the temperature distribution of the flow in the pipe with deposition both in time and along the length and cross-section of the pipe.

The presented diffusion models of crystallization kinetics (4) and deposition of paraffins on the surface of pipes (7,8) are migration-diffusion in nature, where both diffusion of paraffin from the liquid phase to the solid phase and diffusion transfer of paraffin particles to the surface plays an important role. The formation of a dense layer of particles on the surface of pipes is determined by many factors, among which it is important to note hydrodynamic, mass exchange and thermodynamic conditions, rheological properties of the dispersed medium, adhesion compatibility of particles with a streamlined surface, physical and chemical transformations in the boundary layer, particle sizes and concentration, the orientation of the streamlined surface, etc. Analysis of such processes showed that deposition on the inner surface of the pipes to form a dense layer of particles with a low thermal conductivity degrades heat exchange with the external medium, resulting in a decrease in heat transfer and heat transfer coefficients. Introducing a dimensionless thickness of deposits in the form, β = 1−δ_s/R₀, we express the main transfer parameters for small thickness deposits δ_s/R₀ ≤ 0.2 in pipes from β : as heat transfer coefficient for turbulent flow α/α₀≈β^-1.8 and for laminar flow α/α₀≈β^{-3/2; heat transfer coefficient K-1~1/λ_Bln β-1; flow rate V/V₀=β-2; number Re/Re₀=β-1 ; resistance coefficient in pipes atthe laminar flow ξ_L/ξ_L0 = β and turbulent flow ξ_T/ξ_T0= β1/4 (in these expressions the subscript “0” refers to a clean pipe). As follows from these formulas, if, in the case of laminar flow, an increase in the thickness of the deposits in the pipes leads to hydrodynamic instability, then for a turbulent flow, the same factor contributes to an increase in energy dissipation, a decrease in the scale of turbulence and, associated with this, attenuation in the intensity of turbulence. From this, it follows that crystallization, precipitation, and formation of a dense layer on the surface of the pipes have a reverse effect on the flow hydrodynamics and heat - mass transfer in the pipes. If a decrease in the temperature in the core of the flow is observed over time, then the formed paraffin particles together with asphaltenes particles have a significant influence on the structure formation in the flow and thereby change the rheological properties of the oil [31]. Formation of a dense layer of particles of asphalt, and paraffin substances on the surface of pipes significantly affects the change in temperature profile in time, length and radius (13). A decrease in the temperature of the flow in the pipe results in a shift of the crystallization front to the center of the pipe, as a result of which the process of crystallization of paraffins is carried out in the volume of the pipe. The formed paraffin particles in the flow volume can also be transferred diffusely to the pipe surface, confirming the migration-diffusion deposition mechanism. At a high concentration of paraffin particles in the flow volume, it is possible to form coagulation structures that pass into aggregates, clusters of aggregates and eventually form together with particles of asphaltene a frame, leading to an increase in the rheological properties and viscosity of the oil. In the case of coagulation of paraffin particles in the flow volume, their free settling is possible, characterized by a migration-gravitational or mixed mechanism.}

Computational modeling can be a powerful tool for predicting and interpreting wax deposition phenomena after validation with available experimental data. Most laboratory experiments are based on a single-phase flow, which often gives deviations from multiphase flow cases. Simulation results are not always applicable to real field cases. For a more reliable interpretation, the scaling effect must be taken into account. Current research needs to focus on more complex environments. One way to overcome this problem is to validate these models with an additional field dataset.

This work was supported by the Science Foundation of «SOCAR» under the grant project 04LR - AMEA (10/09/2019) at the Institute of Catalysis and Inorganic Chemistrynamed afterAcad. M.F.Nagiyev. The authors are grateful to Professor G.A. Mansoori (University of Illinois at Chicago) for providing extensive information on asphaltenes and other heavy organics in petroleum fluids, as well as for censorious remarks.

1. Beysekov SS, Kurbanov RR (2015) Increasing the oil recovery factor. Journal of JSC "VNIIOENG," Series Construction of Oil and Gas Wells Onshore and Offshore 8: 39-40.
2. Salah, Yaseen, Ali G, Mansoori (2019) Microscopic details of asphaltenes aggregation onset during waterflooding. Petroleum Science and Technology Journal 37(5): 573-580.
3. Huang Z, Zheng S, Fogler HS (2016) Wax deposition: experimental characterizations, theoretical modeling, and field practices. CRC Press, USA.
4. Kuznetsov SV (2016) Investigation of thermophysical processes in the filtration of paraffinic oil to a horizontal well. Abstract dissertation for the degree of candidate of physical and mathematical sciences. Tyumen, Russia, p. 20.
5. Senra MJ (2009) Assessing the role of polydispersity and co crystallization on crystallizing n-alkanes in n-alkane solutions. University of Michigan, USA.
6. Manafov MR, Kelbaliev GI (2020) Analysis of the modern state of researches on deposition of asphalt-resin substances, paraffin and modeling methods. Azerbaijan Chemical Journal 2: 6-19.
7. Musakaev NG (2001) About the mathematical schemes describing the process of wax crystallization in oil-gas wells. Special Issue Proceedings of International Conference RDAMM 6: 2.
8. Volkova GI, Loskutova YuV, Prozorova IV, Berezina EM (2015) Preparation and transportation of problem oils (scientific and practical aspects). TSU Publishing House 136: 9.
9. Mojtaba, Mansourpoor, Reza, Azin, Shahriar, et al. (2019) Experimental investigation of wax deposition from waxy oil mixtures. Applied Petrochemical Research 9: 77-90.
10. Todi S (2005) Experimental and modeling studies of wax deposition in crude oil carrying pipelines. Ph.D. Thesis, University of Utah, Salt Lake City, UT, USA.
11. Marwa, El-Dalatony M, Byong-Hun, Jeon, El-Sayed, et al. (2019) Occurrence and characterization of paraffin wax formed in developing wells and pipelines. Energies 12: 967.
12. Guo B, Song S, Ghalambor A (2014) Chapter 15-Flow assurance. In: (2^nd edn), offshore pipelines. Gulf Professional Publishing, Boston, MA, USA, pp. 179-231.
13. Leporini M, Terenzi A, Marchetti B (2019) Experiences in numerical simulation of wax deposition in oil and multiphase pipelines: Theory versus reality. J Pet Sci Eng 174: 997-1008.
14. Li S, Huang Q, Zhao D, Lv Z (2018) Relation of heat and mass transfer in wax diffusion in an emulsion of water and waxy crude oil under static condition. Exp Therm Fluid Sci 99: 1-12.
15. Zheng S, Saidoun M, Mateen K (2016) Wax deposition modeling with considerations of non-newtonian fluid characteristics. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, p. 18.
16. Lashkarbolooki M, Seyfaee A, Esmaeilzadeh F, Mowla D (2010) Experimental investigation of wax deposition in Kermanshah crude oil through a monitored flow loop apparatus. Energy Fuels 24: 1234-1241.
17. Venkatesan R (2004) The deposition and rheology of organic gels. Dept of Chemical Engineering, University of Michigan, USA.
18. Burger ED, Perkins TK, Striegler JH (1981) Studies of wax deposition in the Trans Alaska pipeline. Soc Pet Eng.
19. Giancarlo, Giacchetta, Barbara, Marchetti, Mariella, et al. (2019) Pipeline wax deposition modeling: A sensitivity study on two commercial software. Petroleum 5(2): 206-213.
20. Noville I, Naveira L (2012) Comparison between real field data and the results of wax deposition simulation. SPE Latin American and Caribbean Petroleum Engineering Conference, Mexico City, Mexico.
21. (2016) Schlumberger, OLGA, User Manual.
22. Rygg PO, Rydahl BA, Rønningsen KH (1998) Wax deposition in offshore pipeline systems [Conference] 1^st North American Conference on Multiphase Technology. Banff, Canada.
23. Rosvold K (2008) Wax deposition models, Master thesis, NTNU, Norway.
24. Hayduk W, Minhas B (1982) Correlations for prediction of molecular diffusivities in liquids. Can J Chem Eng 60(2): 295-299.
25. Aiyejina A, Chakrabarti DP, Pilgrim A, Sastry MKS (2011) Wax formation in oil pipelines: a critical review. Int J Multiphas Flow 37(7): 671-694.
26. Coutinho JA, Edmonds B, Moorwood T (2006) Reliable wax predictions for flow assurance. Energy Fuels 20(3): 1081-1088.
27. Markin AN, Sukhoverov SV (2011) Study of the kinetics of paraffin release from oil. Bulletin of the FEB RAS, 5: 66-71.
28. Kelbaliev GI, Rasulov SR (2014) Hydrodynamics and mass transfer in dispersed media.
29. Kelbaliev GI, Ibragimov Z (2009) Coalescence and fragmentation of droplets in isotropic turbulent flow. Theor Main Chem Tech 43(3): 329-336.
30. Kanevets GE (1982) Heat exchangers and heat exchange systems.
31. Kelbaliev GI, Rasulov SR, Rzayev AG (2016) Modeling of oil filtration in a porous medium and technology of liquid-phase extraction of asphaltenes.Theoretical Foundations of Chemical Engineering 50(6): 573-682.