Micron-scale Monte Carlo Simulations for Additive Manufacturing using Electron Beam

Additive Manufacturing (AM) process is a new technique for building parts layer upon layer by melting fine metal powders. This process can be used to manufacture intricate parts that are impossible to create with standard metal processes, such as casting [1]. Currently there are two methods for metal powder bed AM: laser fusion and Electron Beam Melting (EBM). In this study we focus on the properties of the EBM process when interacting with titanium powder. The EBM system is based on a gun that emits into a vacuum chamber 60 keV electrons, which are directed into the scanning position on the build table using an electromagnetic focusing device. The typical beam current is at ∼30mA and the scan rate is approximately 104mm/s [2].
The typical EMB process utilizes Ti-6Al-4V Titanium powder (Grade 5) (4.43g/cm3), with an average grain size of ∼100μm. A layer of powder is spread on a heated baseplate and then pre heated to about 700 °C; a second pre-heating follows in the region in which full melting is about to occur. Once these two pre-heating steps have taken place, the electron beam selectively melts first the sample circumference, then subsequently the inner part of the sample. The process repeats itself by laying down another layer, pre-heating and melting, until full build achieved.
Numerus studies [3] were conducted on simulation and modelling of the AM process by Selective Laser Melting (SLM), yet few on EBM [4]. Several of these modelling studies set out to resolve a single-track SLM process in a mesoscopic, full-geometry description; based on numerical computing of heat transfer functions [5], they were essential for optimization of AM processes. Alternatively, this current work emphasizes the importance of the heat generated by the electron flux, which, to the best of our knowledge, is the first time this issue has been addressed. The modelling studies will consequently provide a better understanding of the AM process regarding the efficiency of electron energy deposition, generating local heat and heat transport through the powder.
One drawback of the AM process by EBM involves a phenomenon called “black smoke,” that occurs when powder-particles eject from the powder during the interaction of the beam with the raw powder [4,6,7]. This “smoking” emission can potentially intercept the AM process or may even cause failure of the manufactured part.
To simulate the AM process by EBM and to investigate related phenomena, we used the EGS5 Monte Carlo code system [8], in order to take advantage of its electron transport modelling in a 3D geometry. The aim of this EGS5 simulation was to study the “smoking” phenomenon by looking at energy-momentum deposition at the microscale level.

In order to simulate electron interactions with the metal powder bed, we prepared a user-code for the EGS5 Monte Carlo code system [8]. The EGS5 (Electron-Gamma Shower) code system is a general-purpose package for the Monte Carlo simulation of the coupled transport of electrons and photons in an arbitrary geometry for particles with energies ranging from above 1keV up to 100GeV. The EGS5 code computes electron transport in matter as an analog multiple scattering process based on the condensedhistory method (class II) including splitting each step into two segments, after which a scattering hinge is applied between the segments [9]. The EGS5 code system includes several tools, such as the CG-VIEW that is used for geometry editing and as a viewer, and the PEGS5 editor for media cross-section definition. The EGS5 code system has been used in a wide variety of applications, particularly in medical physics and radiation measurement studies. In recent years, the use of EGS5 for dosimetry calculations in the field of medical physics has been proven successful as has been shown in several studies [10-14].
All kinetic energy cut-offs throughout this study were set at 1keV. The electron beam source was defined in the code as a randomly initiated parallel beam aimed toward a titanium ball into an opening with a radius of 70μm. The geometry of the simulation consisted of a vacuum chamber and a 50μm radius pure solid titanium ball, which represented a single-powder particle. Simulations in this work were carried out in two different modes: 1. A few electrons emitted for the purpose of viewing their tracks in the geometry using CG-View; 2. A large number of histories to obtain electron-scattering distributions.

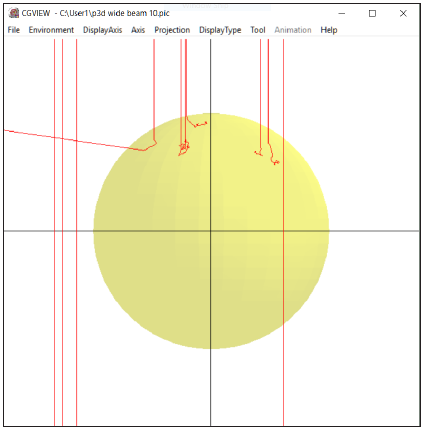
In order to observe electron tracks performance, ten electrons were initiated, and each step was registered throughout the simulated system. In Figure 1 several cases are observed: 1. Straight lines of electrons that missed the object; 2. Curved lines inside the object where electrons penetrated the object and interacted with matter; 3. A straight line of outgoing electrons that backscattered from the object.

Figure 1: Track view using CGVIEW of ten sampled electrons: The ball is the titanium particles, and the lines represent electron tracks. Several electrons hit their target, while one backscattered electron is shown.

Only about 65% of the penetrating electrons are completely absorbed by the body. Electrons that were scattered deposited around 15-20keV to the titanium body, although obtaining their direction requires more investigation. Another simulation with 106 histories in precise conditions was carried out in order to score the directional distribution of scattered electrons. For this simulation the tracking option was turned off, since too many data lines could be unnecessarily produced. Figure 2a evinces the scattered electron directional distribution on a cylindrical surface surrounding the body. The Z-axis starting point is in front of the body center. These results were arranged in angular distribution fashion, as presented in Figure 2b.

Figure 2:A. Scattered electron directional distribution on a cylindrical surface surrounding the body, with the Z-axis starting point in front of the body center; B. The distribution results arranged in an angular plot.

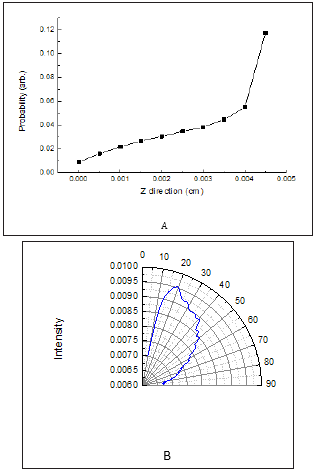
Figure 3: Momentum vector definition in spherical system: Pe - initial electron beam vector; Pbody - body vector; P’e - scattered electron vector.

The scattered electron angular distribution results indicate that most electrons scattered toward the angular range of 15°-50°. Once the emitted electrons versus the angle were collected, the momentum vector P’_e direction could be obtained, as defined in the illustration in Figure 3 with the initial electron momentum vector represented by P_e, and P_body as the momentum transferred to the body.
Most scattered electrons are transmitted toward small angles. The initial electron energy and direction are known, and the scattered electron momentum can be extracted from the Monte Carlo simulation results, as shown below. In addition, energy deposition to the body was tallied.
In order to obtain body momentum using the initial parameters and simulation results, relativistic formalism is essential, as in the following formulation.
Initial electron momentum is based on equation 1:

P =γ m0v Eq. 1

Electron momentum based on energy is:

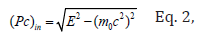
Finally, scattered electron outgoing momentum is:

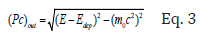
Subtracting the length of the two vectors provides the body momentum:

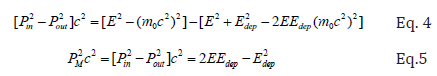
It can be seen from Eq.5 that the body momentum after scattering is solely dependent on initial electron energy and energy deposition into the body. Both numbers are known: E is the defined beam energy set-up, and Edep was calculated using the MC simulation.
While the electron energy deposition to the body provides heat, and eventually melting, the momentum gain of the body will lead to its motion. Those bodies that were not melted and were not attached to their neighbors can be pushed by the available momentum outside the powder layer. As previously reported [4,15], one of the reasons for “smoking” was powder particle electric charging, and the powder particle lifting force was compared to a gravitational force that holds the body steady in the powder during the AM process. If we assume similar considerations, then one body mass is about 2.4 micro-grams, 0.01cm height lifting, acquire 2.35E-05 erg potential energy (by using the gravity g constant). On the other side, the momentum transfer corresponds to about 20keV, consisting of 3.2E-08 erg. Hence, on average an amount of one thousand electron collisions could separate a single titanium body from the powder layer top.
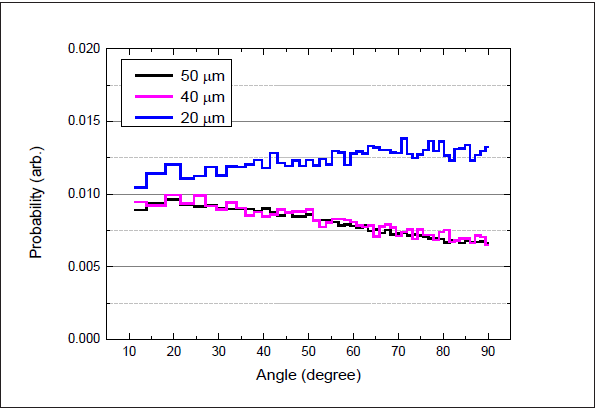
Since the titanium particles size can be distributed, we simulated two more cases: 40μm and 20μm radius pure solid titanium balls, in front of 40μm and 20μm radius beam opening, respectively. Scattered electron directional distributions for each case are shown in Figure 4: The 50μm and 40μm titanium particles obtained the same results, and the 20μm titanium particles obtained different angular dependence where scattering became higher toward 90°. We can learn from these results that momentum transmission for smaller particles is much more able to raise the “smoking” effect.

Figure 4: Scattered electron angular distribution for three different particle sizes: 50, 40 and 20μm. The electron beam radii are equal to each particle radius.

The Monte Carlo simulation performed in this study revealed the following: energy deposition, scattering direction distributions, and visualization of electron tracks along the system. Kinematic considerations were calculated based on MC results, and the momentum vector was formulated based on principles of relativistic energy-momentum conservation formalism.
Electron momentum is transferred to the particle in different ways: downstream electrons toward the particle’s center contribute the melting, while some electrons that hit the sides raise particle scattering to the sides (as illustrated in Figure 1). Powder particle electric charging was proposed [4] as one reason for “smoking”; however, this phenomenon might rather be due to a combination of kinematics and electric potential causing titanium bodies to leap out of their position. In conclusion, the “black smoke” phenomenon can be assessed as resulting due to beam collisions with powderparticles in the layer top.
Further studies using the EGS5 Monte Carlo code system for modelling of the EMB process will shed more light on furthermore aspects.

1. Ian Gibson, David WR, Brent S (2010) Additive manufacturing technologies. Electronic ISBN: 978-1-4419-1120-9, Springer USA.
2. http://www.arcam.com/
3. DebRoy T, Wei HL, Zuback JS, Mukherjee T, Elmer JW, et al. (2018) Additive manufacturing of metallic components - Process, structure and properties. Progress in Materials Science 92: 112-224.
4. Cordero ZC, Meyer HM, Nandwana P, Dehoff RR (2017) Powder bed charging during electron-beam additive manufacturing. Acta Materialia 124: 437-445.
5. King W (2015) Overview of modelling and simulation of metal powder bed fusion process at Lawrence Livermore National Laboratory. Materials Science and Technology 31(8): 957-968.
6. Klassen A, Bauereiss A, Korner C (2014) Modelling of electron beam absorption in complex geometries. J Phys D 47(6).
7. Scharowsky T, Osmanlic F, Singer RF, Korner C (2014) Melt pool dynamics during selective electron beam melting. Appl Phys A 114(4): 1303-1307.
8. Hirayama H, Namito Y, Bielajew AF, Wilderman SJ, Nelson WR (2006) The EGS5 code system. SLAC-R-730 / KEK Report.
9. Bielajew AF, Wilderman SJ (2000) Innovative electron transport methods in EGS5. Proceedings of the 2^nd International Workshop on EGS, KEK, Japan KEK Proceedings.
10. Tsuji S, Narihiro N, Oita M (2014) Absorbed dose conversion factor in the farmer type ionization chamber. Proc. of the 21^st EGS Users' Meeting in Japan, p. 25.
11. Takeuchi A, Raich T, Yoshida R, Kojima K, Niwa M, et al. (2013) Effect of the difference in electron cut off energy on surface dose calculation in the monte carlo linear accelerator simulation of megavoltage photon beams. Proc. of the 20^th EGS Users' Meeting in Japan, p. 30.
12. Kondo S, Haba T, Hayashi D, Numamoto H, Ishii T, et al. (2012) Verification of pin-photo diode detector characteristics using EGS5. Proc. of the 19^th EGS Users' Meeting in Japan, KEK Proc 2012-7, p. 16.
13. Kumagai S, Okajima M, Takaya H, Arai N, Waga K, et al. (2012) The improvement of discrepancy between radiotherapy treatment planning system and verification system using Effective Density Method. Proc. of the 19^th EGS Users' Meeting in Japan, KEK Proc 2012-7, p. 66.
14. Rachi T, Iwamoto Y, Tamura M, Ota K, Shimosato T, et al. (2012) Study of collimator scatter factor (Sc) and phantom scatter factor (Sp) using Monte Carlo simulation. Proc. of the 19^th EGS Users' Meeting in Japan, KEK Proc 2012-7, p. 76.
15. Qi HB, Yan YN, Lin F, He W, Zhang RJ (2006) Direct metal part forming of 316L stainless steel powder by electron beam selective melting. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture 220(11): 1845-1853.