- Submissions

Full Text
Research & Development in Material Science
Synthesis, Vibrational Analysis, Optical, Ionic Conductivity and Conduction Mechanism of γ-NaCoPO4 Compound
Asma Ajmi1, Karoui K1*, Khirouni 2 and Ben Rhaiem A1
1Faculty of Sciences, University of Sfax, Tunisia
2Faculty of Sciences of Gabes, Laboratory of Physics of Materials and Nanomaterials Applied to the Environment, Tunisia
*Corresponding author: Karoui K, Faculty of Sciences, University of Sfax, Tunisia
Submission: April 01, 2020;Published: April 16, 2020

ISSN: 2576-8840 Volume 13 Issue 1
Abstract
Sodium cobalt monophosphate (γ-NaCoPO4) compound was synthesized by a solid-state reaction. X-ray powder diffraction analysis indicated that this sample is well crystallized in the monoclinic system Zéolite ABW structure with P21/n space group. The vibrational study showed the appearance of the tetrahedral PO4 and its vibrations. The electrical measurements of this compound were analyzed by complex impedance in the frequency range (43Hz-102MHz) at several temperatures. Nyquist plot at several temperatures revealed a single semicircle associated to the grains. The temperature dependence of the conductivity for the grain obeys to the Arrhenius law. The AC conductivity is insured by a process defined as a hopping transport mechanism. The thermal behaviors of the exponent ‘S’ indicate that the Correlated Barrier Hopping model (CBH) is the most dominant mechanism. The analysis of the data unfolded that the optical gap energy is determinate using Kubelka-Munk function and the value of Urbach energy is equal to 0.395eV.
Keywords: X-Ray diffraction; FT-IR FT-Raman spectroscopies; Impedance spectroscopy; Optical properties
Introduction
Over the most recent couple of years, phosphate compounds have been the subject of numerous investigations for their potential applications in diverse areas such as solid-state laser materials, solid-state batteries, sensors, ionic conductors and catalysts [1-4].
Among them, we interestingly to orthophosphates with the general formula ABPO4 (A: monovalent cation and B: divalent cation) regarding these monophosphates crystallize with different structural types such as olivine, maricite, arcanite, tridymite, glaserite, etc. [5].
The formation of α-NaCoPO4 was reported by Hammond et al. [6], its crystallizes in the space groupe Pnma which are composed by edge-sharing chains of CoO6 octahedral cross -linked by PO4 tetrahedral, and sodium ions Na+ are located in 10-coordinate cavities. The β-NaCaPO4 is indexed in the hexagonal with space group P61 and P65 [6]. This structure consists of P and Co atoms occupying tetrahedral sites and the Na atoms located in the cavities of tetrahedral framework. The γ-NaCoPO4 phase is indexed in the monoclinic system with space group P21/n [7]. The phosphorus atoms and the cobalt atoms are located in tetrahedral site, the sodium atoms are located in the channels. In the red phase, the fourth polymorph, cobalt is in trigonal bipyramids connected with PO4 tetrahedral to form a framework with one-dimensional channels in the space group P21/c [8].
In our research, we mainly interested on the compounds α-NaCoPO4, β-NaCoPO4 and γ-NaCoPO4 given the difference in the structure of these compounds which can influence in the optical and electrical properties. In these works I’m interested by the studies of the γ-NaCoPO4 compound which can be distinguished by its layered crystal structure and high polarizability of Na+ ion. The formation of the crystal structure of γ-NaCoPO4 was reported by Chippindale et al. [7] which is isostructural with NaZnPO4 and crystallizes in the monoclinic system ( P21/n space group ) and cell parameters: a=5.221(1) Å, b= 9.983(1) Å, c= 7.388(1) Å and β=90.210(4) [7]. The structure characterized by CoO4 and PO4 tetrahedral, respectively. The CoO4 tetrahedron has roughly a standard geometry, with a mean Co-O bond length of 1.962Å. The PO4 tetrahedron also has an around regular geometry, with a mean P-O bond length of 1.535Å (Figure 1) [7]
Figure 1: Structure of the γ-NaCoPO4 viewed down the [100] direction.
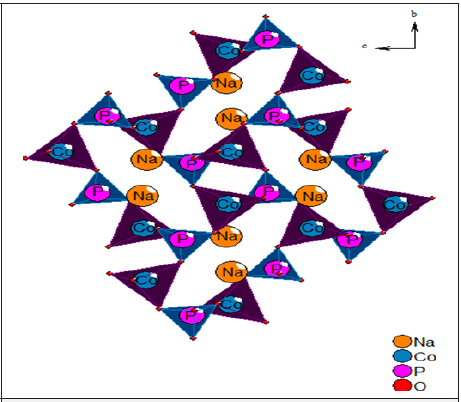
The utmost objective of this paper is to study the electrical properties of γ-NaCoPO4 compound as a function of frequency and temperature. Also, this study may give valuable information on the electrical conductivity and conduction mechanism for this sample. Moreover, the optical properties are reported.
Experiment
The cobalt sodium orthophosphate was carried out by the ceramic method. The raw materials of high purity (≥99%) are Na2CO3, Co2O4 and NH4H2PO4. These stoichiometric amounts of the reactants were determinate according to the chemical equation
2NH4H2PO4 + Na2CO3 +Co2O4 →2NaCoPO4 + 2NH3 + 3H2O +CO2These precursors were thoroughly ground in a mortar to obtain a fine powder. In the first step the homogenized powder was calcined in an electric furnace at a temperature of 673K for 16h, in order to exhaust NH3, CO2, and H2O. Further, the annealed powder was grounded again, and then pressed into cylindrical pellets using 3T/cm2 uniaxial pressure. Finally, the obtained pellets were sintered at a temperature of 1023K for 4 days.
Sample characterizationTo ensure the phase purity of the compound γ-NaCoPO4, X-ray powder diffraction (XRD) was checked out. It was undertaken using Phillips powder diffractometer with CuKα radiation (λα1=1.5056Å, λα2=1.54446 Å) recorded at room temperature over a wide range of Bragg angles (20°≤2θ≤80°). The Rietveld refinement of the XRD profile was performed using the Fullprof program.
On the other hand the infrared spectrum was obtained using a Perkin Elmer FT-IR1000 in the range (1400-400cm-1).The Raman spectroscopy was recorded at room temperature in the range (50- 1400cm-1) where it was measured using a single monochromatic spectrophotometer Notch filter (Labram HR800). These two techniques were used to confirm the presence of grouping (PO4)3-.
To effectuate the electrical conductivity measurements, the powder was pressed in order to obtain a circular disc with 8mm in diameter and 1.2mm in thickness. Their opposite sides of this pellet were inserted between two platinum electrodes. The transport properties of the sample were performed using a Tegam 3550ALF impedance analyzer operating over a frequency range 43Hz-102MHz and at temperature 460- 620K. Optical absorption spectrum was examined at room temperature using (UV-vis SCANNIINGSPECTRO-PHOTOMETER) scanning spectrophotometer in the range of wavelength (200-800nm).
Results and Discussions
Figure 2: X-ray powder diffraction pattern of γ-NaCoPO4: experimental data (the point symbols), calculated data (the solid lines), difference between them is shown at the bottom of the diagram Bragg positions are marked by vertical bar and the peak identified by asterisk indicate the impurity phase of Na4Co4(PO4)4 and Na24Co24 (PO4)24.
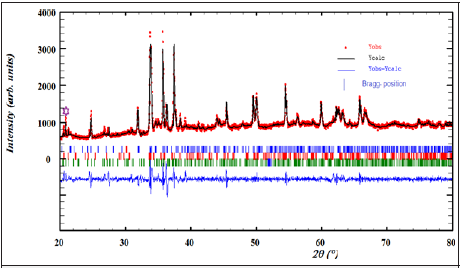
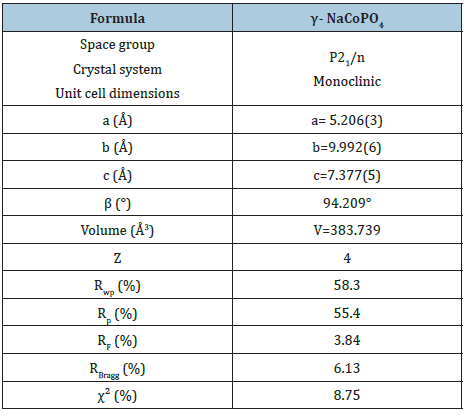
The diffractogram of X-ray of γ-NaCoPO4 sample checked at room temperature is illustrated in Figure 2. The refinement for the ceramic was performed by the Rietveld refinement technique using Fullprof software [9,10]. As seen in Figure 2 a good fit between the calculated and observed profiles. In fact, the best refinement of the experimental profile was obtained in the monoclinic system with P21/n space group. The obtained reliability factor and lattice parameters of γ-NaCoPO4 are provided in Table 1. Consequently, the unit cell parameters were in good accordance with those reported by Chippindale et al. [7].
Table 1: Crystallographic data of the structure refinement of γ- NaCoPO4 at 300K.
We can notice the presence of a small extra peak identified by asterisk in the X-ray powder pattern (Figure 2) indicating the presence of impurity of Na4Co4(PO4)4 and Na24Co24 (PO4)24 which crystallizes in the monoclinic and hexagonal system, respectively.
Vibrational studyIn order to obtain information about the symmetry and the chemical bonding of the PO4 group, it is interesting to study the vibrational spectra of this compound.
Figure 3: Exhibits the Raman spectrum measured between 50 and 1500cm−1 and FTIR spectrum in the region (400-1400) cm−1 of the investigated compound.
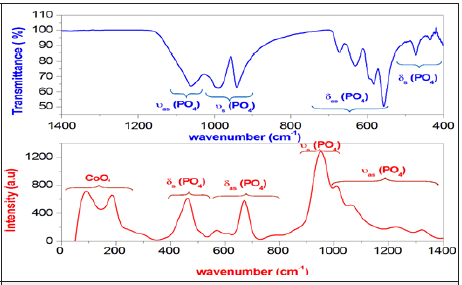
The Raman and Infrared spectrum of γ-NaCoPO4 compound, obtained at room temperature, is represented in Figure 3. The attributions of these bands is dared by comparison with the other orthophosphate [11,12]. Previously, in the low-frequency region of the spectrum, the bands are mainly due to the internal modes of the CoO4 tetrahedral [13] Besides, the bands observed at 434, 457 and 474cm-1 are related to the symmetric deformation 𝛿s of PO4. In fact, the bands situated between 557 and 673cm-1 are attributed to the antisymmetric bending vibration 𝛿as of PO4. Furthermore, the band observed at 941 and 989cm-1 are attributed to the symmetrical stretch υs vibration of the tetrahedral PO4. Although the band located in the region (1015-1323)cm-1 due to the antisymmetric stretching υas of PO4. These bands assignments are gathered in Table 2.
Table 2: Vibrational spectra data (cm-1) and band assignments for the title compound.

Complex electrical impedance analysis
Equivalent circuit: The impedance spectroscopy is one of the most adequate techniques to investigate the electrical conductivity and analyze the charge transport processes in the grain; grain boundary and electrode effect in materials for both wide frequency and temperature ranges [14].
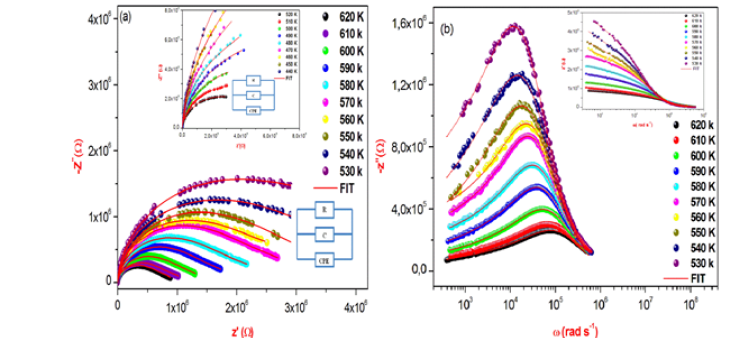
In this work, the Nyquist plots (-Z” vs Z’) of γ-NaCoPO4 recorded at different temperatures in well-defined range of frequency is illustrates in Figure 4a. From the shape of these plots, this compound formed by a single semi-circular arc associated the contribution of the grain. Based in the Z-View-software, these spectra were modeled by an equivalent circuit which is collected of a parallel combination of resistance Rg (bulk resistance), capacitance (Cg) connected to constant phase element (capacity of the fractal interface CPE).
The fitted values obtained by the equivalent circuit are used to simulate the experimental curve of real and imaginary part of impedance spectroscopy based on the fallowing equation: (2) and (3)

The great conformity of the calculated lines (simulated curve) with experimental data observed in Figure 4b indicates that the chosen equivalent circuit is well described the behavior of this material. The real part of impedance decreases with the rise of frequency. This plot shows that conduction increases with the rise of temperature and frequency.
In the imaginaire impedance, we observed that the magnitude of Z″ decreases with the increase in temperature and the peak frequency shifts to the higher values. These spectra are characterized by the appearance of the maximum value Z”max at a certain frequency ωmax, to introduce the relaxation time η from the condition (ωmaxη=1)
Figure 4a & 4b: Complex impedance spectra at different temperatures, the solid line are a fit of the experimental data and variation of real and imaginary part of the impedance as a function of frequency for some representative temperature.
Dc conductivity: The conductivity of the grain was determined at each temperature from the data fit of the impedance spectrum by the following relation
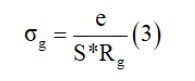
With e is the thickness of the pellet, S is the area of the electrode deposited on the pellet and R is the value of the resistance determined by the adjustment.
Figure 5: Variation of the Ln (ζg) as function of temperature of γ-NaCoPO4.
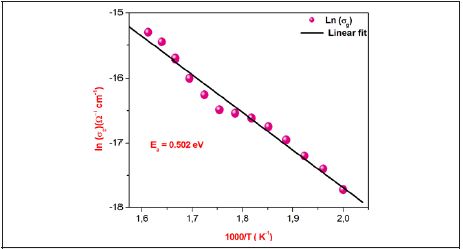
The temperature dependence of the grain conductivity ln(𝜎g) for γ-NaCoPO4 is embodied in Figure 5.
We also noted that the obtained curves increase linearly with the increasing temperature which indicates that the electrical conduction in this material is a thermally activated transport process characterized by Arrhenius law of the following form

W h e r e A i s t he pre-exponential factor, kB is the Boltzmann constant and Ea is the activation energy for the mobile ions. Additionally, in this material we observed continuities in the studied temperature range. Following Arrhenius equation, the calculated activation energies from a linear fit of the experimental data is Ea=0.502eV.
AC conductivity studies: As a matter of fact, the value of ac electrical conductivity was obtained from the real (Z’) and imaginary (Z”) parts of the impedance data using the relation [15]:
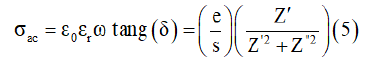
Where Z′ and Z” are the real and the imaginary parts of complex impedance, respectively. S is the cross-sectional area of the electrode deposited on the sample and e is the thickness of the pellet. Added to this, we noticed the increase conductivite with the angular frequency at higher angular frequency region for different temperatures of γ-NaCoPO4 compound. So, this behavior can be generally analyzed by Joncher’s law according the Eq
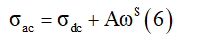
With σdc is the value of the direct current conductivity, A is a constant for a particular temperature and S is the power exponent.
Based on the Jonsher equation (7) we observe the good conformity between the theoretical curve and the experimental result which allows us to determine the parameters ζdc, A and s at several temperatures. Figure 6a illustrated the variation of the electrical conductivity (ζac) en function of frequency angular at selected temperatures. From the ac conductivity spectra we distinguish the presence of two distinct regions:
Figure 6a & 6b: Frequency dependence of AC conductivity at various temperatures and variation of Ln (ζdc) as function of temperature

Firstly, at a low frequency region of the conductivity spectra shows the frequency independent behavior which suggests that the ions perform uncorrelated and random hopping motions, leading dc conductivity [16]. Secondly, after a critical or hopping frequency of the charge carriers, conductivity increases sharply with increasing frequency and shows a larger dispersion [17].
Figure 6b gives the variations of the direct current conductivity as function temperature and show that the conductivity increase with temperature which reveals a typical Arrhenius-type behavior [18].
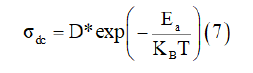
Where σdc is the direct current conductivity, D is the preexponential factor, and Ea the thermal activation energy for the ion migration.
The activation energy value obtained from linear fit of data points is Ea=0.52eV.
Figure 7a shows the master plots of the normalized imaginary electric modulus and normalized frequency. The superposition of all curves at different temperatures suggests that the same thermal activation energy is involved in the dynamic processes that occur in the system and that the conduction mechanism remains unchanged over the temperature range under study [19].
Conduction mechanism: In order to better understand the conduction mechanism in our materials, several models such as the Correlated Barrier Hopping (CBH) model, suggested by Elliot, the Quantum Mechanical Tunneling (QMT) model, by Austin-Mott, the Non-overlapping Small Polaron Tunneling (NSPT) model and the Overlapping Large Polaron Tunneling (OLPT) model proposed by Long [20-23]. These theoretical models correlate the conduction mechanism of the AC conductivity with the parameter behavior S (T).
In the present case, Figure 7b represents the temperature dependence of the exponent ‘S’ for the studied sample, which clearly exhbit that S decreases with the increase of temperature. The Correlated Barrier Hopping model (CBH) is used for several materials. In this model the conduction occurs by a jump of a single polaron (single polaron) or by a correlated jump of two polarons (bipolaron) on the Coulomb barrier separating two neighboring sites.
Figure 7a & 7b: Variation of exponent (s) as function of temperature and modulus scaling behavior in to a master curve of investigated compound at different temperatures.

In order to differentiate between the transfer by a single or two polarons, we calculate ωM from the slope of the curve (1-s)=f(T), thus for ωM=Ea/4 we are in the case of a single polaron and for a bipolaron we have ωM=Ea/2 [24].
In this model, the AC conductivity is given by [25]:
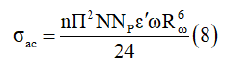
Where
n is the number of polaron involved in the hopping process.
ε’ is the dielectric constant for a fixed frequency value.
NNp is proportional to the square of concentration of states.
NNP=NT (for bipolaron hopping)
NNp = 2 T N Ueff e2KBT − (for single polaron hopping)
Where:
NT is the number of density of states.
Ueff is the effective correlation energy (correlation between electron-phonon), which can be negative whether the electronphonon interaction is sufficiently strong.
For the condition ωη=1, the hopping distance Rω is given by the expression [26]:
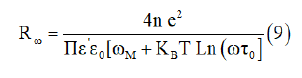
Where τ0 is the characteristic relaxation time for the material and ωM is the height of maximum barrier.
Based on this model, the exponent S has been calculated from the following equation [27]
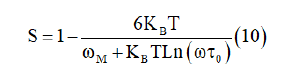
For first approximation of this equation, it becomes
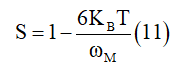
Figure 8a & 8b: Comparative analysis of theoretical AC conductivity for γ- NaCoPO4 at fixed frequencies and the variation of the tunneling distance Rω as a function of temperature at different frequencies of the title compound.

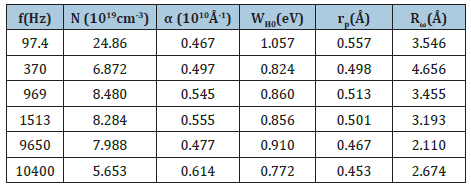
In the present case, the calculated curves of Ln (ζAC) versus 1000/T at some fixed frequencies is given in Figure 8. This suggested a good agreement between the theoretical and the experimental result. It is evident from this figure that 𝜎ac increases linearly with the temperature, implying that the AC conductivity is a thermally activated process. The calculated parameters by the CBH model are listed in Table 3.
Table 3: Parameters obtained from the OLPT model by least squares adjustment.
Modulus analysis
The complex modulus (M”) is defined through this equation:
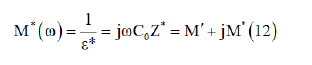
Where M’(real part of modulus) =ωC0Z” and M”(imaginary part of modulus) = ωC0Z, C0= is
the geometrical capacitance= (ε0=permittivity of free space, A=area of electrode surface, and e= thickness). The simulation of the imaginary part of modulus M” allows determining some characteristic parameters of the charge carriers by using the Bergman equation [28]
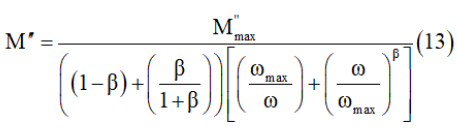
Where Mmax and ωmax are the peak maximum of the modulus and the peak angular frequency of the imaginary part of the modulus, respectively.
The variation of the imaginary and real part of the modulus as a function of frequencies for some representative temperatures is displayed shown in Figure 9a & 9b respectively.
Figure 9: Frequency dependence of the imaginary and real part of electric modulus at different temperatures.
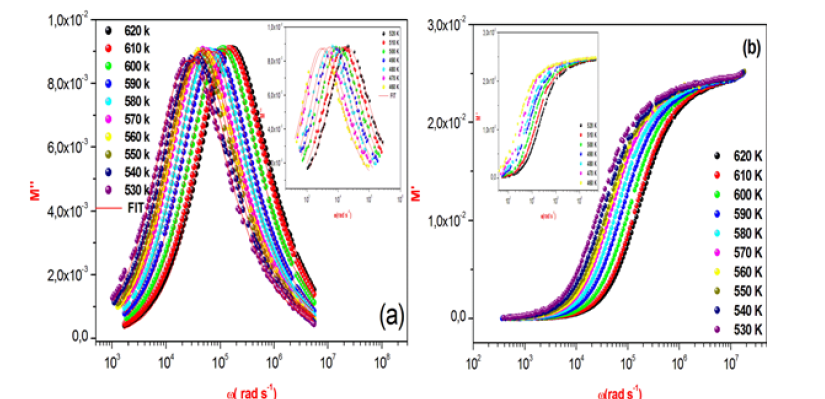
This figure obviously shows a very low value of M’ in the low frequency region. This behavior can be clarified by the lack of a force that governs the mobility of charge carriers under the influence of an electric field [29]. Furthermore, an increase of the value of M” with increasing frequency at different temperatures has been observed. This graph shows that the modulus peaks shift towards higher frequency side when temperature increases. In addition, the appearance of a single peak in the modulus spectra is an indicator of the conductivity relaxation processes.
The relaxation frequency fp extracted from the fit of the modulus is presented as a function of (1000/T) in Figure 10 follows the Arrhenius relation
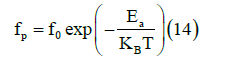
Figure 10: Dependence of Ln (fp) versus reciprocal temperature for γ-NaCoPO4.

Where f0 is the frequency at infinite temperature and Ea is the activation energy. The value of the relaxation frequency fp increases with the increase of temperature. The activation energy of the grain calculated from the slope of the plot is equal 0.614eV, which is different compared to the one obtained for conduction (Ea=0.502eV). This affirms that the conduction in the compound is not predicted by the classical hopping model.
Permittivity formalismThe complex permittivity formalism is an important source to reveal significant information about conduction processes. The complex dielectric response is expressed by two parts [30]:
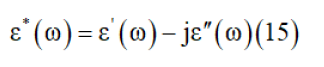
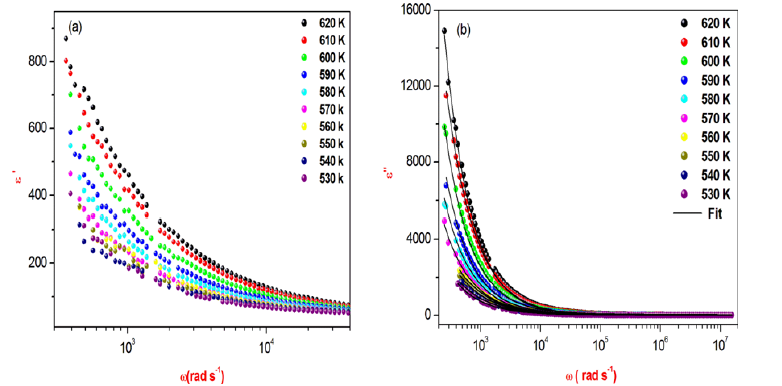
Where ε′(ω) and ε″(ω) are the real and imaginary parts of the dielectric constant, respectively. Figure 11a & 11b illustrates the variation of ε′(ω) and ε″(ω) with frequency at different temperatures. In this compound, the dielectric relaxation is described by a Cole-Cole model giving the frequency-dependent complex permittivity in the form that follows [31]
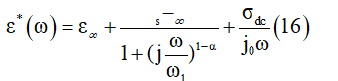
Figure 11: Frequency dependence of the real and imaginary part of the permittivity for the title compound at several temperatures.
Where εs is the static permittivity, ε∞ is the permittivity at infinitely high frequencies, ε0 is the permittivity of the free space, ω1 is the relaxation angular frequency of the Debye process, α is the Cole-Cole parameter and ζdc represents the specific conductivity.
The imaginary part of ε″ is expressed by the follows equation
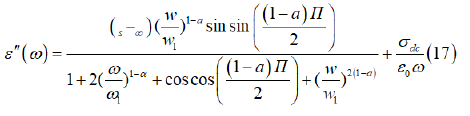
Where α represents the tilting angle (απ/2) of the circular arc from the real axis in the complex permittivity plane.
The first part of equation (22) is related to the dipole reorientation polarization and the second one to the electrical conductivity.
The frequency dependence of the imaginary part ε″ at different temperatures illustrate in Figure 11b.
There are no appreciable relaxation peaks in the frequency range employed in this study. The dielectric loss rises sharply at low frequency, indicating that electrode polarization and space charge effects have occurred, confirming non-Debye dependence. It is obvious from Figure 11a that ε′ decreases with an increase frequency, which can be explained by means of the dielectric polarization mechanism of the material. The high values of ε’ values may be interpreted as the accumulation of charges at the interface between the sample and the electrode, i.e., space charge polarization.
Absorbance spectraUV-Visible spectroscopy: Optical properties are one of the most important factors to evaluate the light efficiency. The ultraviolet-visible (UV-VIS) spectroscopy was used to investigate the change in the optical energy gap, and the Urbach energy.
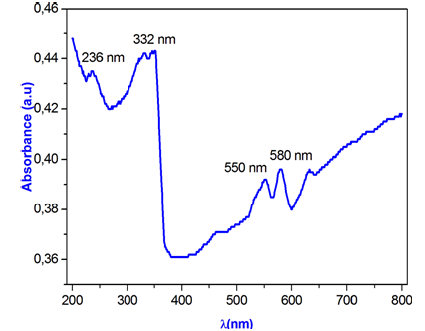
The absorbance spectra of γ-NaCoPO4 was performed at room temperature in the wavelength range (200-800nm) illustrated in Figure 12. The UV-vis spectrum of γ-NaCoPO4 sample exhibit four peaks of absorption at 236nm, 332nm, 550nm and 580nm: The bands with maximum energies at 236nm (5.25eV) can be assigned to the absorption of a highest energetic level in the conduction band. The observed band at 332nm (3.73eV) is due to the 1A1 to 1T2 transition. This conduction band is assigned to the charge transfer from the oxygen to the central phosphate atom inside the [PO4]3- groups [32,33]. The wide band in the range of 550-700nm (2.25-1.77eV) is attributed to 4A2 to 4T1 (P) transition and show the tetrahedral oxygen environment of Co (II) [33].
Figure 12: Frequency dependence of the real and imaginary part of the permittivity for the title compound at several temperatures.
Optical band gap
The relation between the absorption coefficient (which is determined by the kubel Munk function), the energy of the energy band Eg and the corresponding coefficient (p) which is associated to an electronic transition is given by the Tauc equation [34].
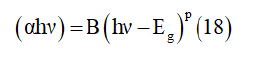
Where α is the absorption coefficient, (hν) is the incident photon energy, B is a constant characteristic of the material and p is equal to 2 for an indirect transition ( plotted as (ahν)1/2 as function hν (Figure 13) or p is equal ½ for a direct transition ( plotted as (ahν)2 as function hν (Figure 13)
The energy of the incident photon is calculated using the equation [35]:
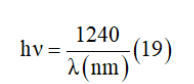
Optical band gap Eg can be determined from the extrapolation of the linear region of the curve to meet the (hυ) axis at (ahυ)2 and (ahυ)1/2=0 [36]. Figure 13 indicates the direct and indirect band gap and the R factor which indicate the better fitting. The best fit that has a value of R close to 1 found by the indirect gap energy and indicate that the gap energy is equal to 3.5±0.03eV.
Figure 13: Dependance of (F(R)*hν)1/2 on the photon energy of γ-NaCoPO4.

Urbach energy
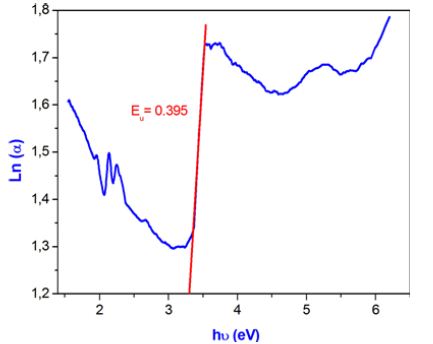
The Urbach energy Eu is a very essential parameter for the characterizations of the disorder of a material which corresponding to transitions between the extended states of the valence band and the localized states of the conduction band.
The Urbach energy tailing which depict the degree of disorder in crystallization of the material is expressed by the empirical formula [37].
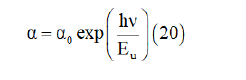
Where 𝛼0 is a constant, 𝐸𝑢 is the Urbach energy.
Taking the logarithm of the above equation for trace the variation of ln (α) as a function of energy (hν).
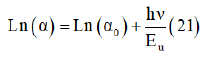
Therefore, the value of Urbach energy (EU) can be calculated from the inverse of the slope of the straight line of plotting Ln (α) as function he incident photon energy (hν) (Figure 14) which is equal 0.395eV.
Figure 14: Plot of Ln (α) versus (hν) of the title compround.
Conclusion
In summary, the γ-NaCoPO4 monophosphate was prepared by the solid state reaction X-ray diffraction demonstrates that the sample crystallizes in the monoclinic system with P21/n space group. Moreover, the analysis of the Nyquist plots allowed determining an equivalent electrical circuit for the title compound which is formed by the parallel combination of resistance (Rg), capacitance (C) and the constant phase element (CPE). Also, the high frequency dependent AC conductivity of sodium cobalt orthophosphate is interpreted using the universal Jonscher’s law. In addition, the temperature dependence of the exponent s reveals the conduction mechanism is explained by CBH model. The dielectric data have been analyzed in modulus formalism, indicating the existence of an only relaxation peak. UV-Vis spectroscopy was investigated to decide certain main parameters, for example, the, the band gap energy and the Urbach energy. The γ-NaCoPO4 compound exhibit excitation bands at 236nm, 332nm, 550nm and 580nm. The band gap energy and Urbach were 3.14eV and 0.4eV respectively.
References
- Sawada A, Azumi T, Kuroiwa Y (2000) X ray study of extremely slow transition in CsZnPO4 Ferroelecrics 237: 245-252.
- Ben Yahia H, Gaudin E, Darriet J (2007) Structure and magnetic properties of the new phosphate RbMnPO4. Journal of Alloys and Compounds 442: 74-76.
- Minakshi M, Singh P, Appadoo D, Martin DE (2011) Synthesis and characterization of LiNiPO4 for aqueous rechargeable battery. Electrochimica Acta 56(11): 4356-4360.
- Navarro M, Ginebra M, Clement J, Martinez S, Avila G, J, et al. (2003) Physicochemical degradation of titania‐stabilized soluble phosphate glasses for medical applications. Journal of the American Ceramic Society 86: 1345-1352.
- Ben Yahia H, Shikano M, Essehli R, Belharouak I (2016) Single crystal structures of the new vanadates CuMgVO4 and AgMgVO4. Materials Chemistry and Physics 178: 128-132.
- Hammond R, Barbier J (1996) Structural chemistry of NaCoPO4. Acta Cryst B 52: 440-449.
- Chippindale M, Cowley R, Chen J, Gao Q, Xu R (1999) A new modification of NaCoPO4 with the zeolite ABW structure. Acta Cryst C 55: 845-847.
- Feng P, Bu X, Stucky GD (1997) Synthesis, crystal structure, and magnetic properties of a new polymorphic sodium cobalt phosphate wth trigonal bipyramidal Co2+ and a tunnel structure. Journal of Solid State Chemistry 129: 328-
- Rietveld HM (1969) A profile refinement method for nuclear and magnetic structures. J Appl Crystallogr 2: 65-71.
- Rodriguez-Carvajal J (1993) Recent advances in magnetic structure determination by neutron powder diffraction. J Phys B 192: 55-69.
- Miladi L, Oueslati A, Guidara K (2016) Phase transition, conduction mechanism and modulus study of KMgPO 4 RSC Advances 6: 83280-83287.
- Irma Botto L, Vassallo M (1989) The vibrational spectrum of the NaZnPO4 ferroelectric phase. Matterials Science 8: 1336.
- Glamazda A, Choi K, Lemmens P, Choi W, Jeen H, et al. (2015) Structural instability of the CoO4 tetrahedral chain in SrCoO3−δ thin films. Journal of Applied Physics 118: 085313.
- Hill R, Jonscher A (1979) DC and AC conductivity in hopping electronic systems. Journal of Non-Crystalline Solids 32: 53-69.
- Yakuphanoglu F, Aydogdu Y, Schatzschneider U, Rentschler E (2003) DC and AC conductivity and dielectric properties of the metal-radical compound: Aqua [bis (2-dimethylaminomethyl-4-NIT-phenolato)] copper (II). Solid State Commun 128: 63-67.
- Dyre J, Shroder T (2000) Universality of ac conduction in disordered solids. Reviews of Modern Physics 72: 873-892.
- Rhouma F, Dhahri A, Dhahri J, Valente MA (2012) Dielectric, modulus and impedance analysis of lead-free ceramics Ba8La0.133Ti1−xSnxO3(x=0.15 and 0.2). Applied Physics A 108: 593-600.
- Jaschin P, Varma K (2017) Lithium ion conductivity and dielectric relaxation in dendritic nanostructured LiTaO3 glass-nanocrystal composites. Journal of Applied Physics 121: 094101.
- Migahed MD, Bakr NA, Abdel-Hamid MI, EL-Hanafy O, El-Nimr M (1996) Dielectric relaxation and electric modulus behavior in poly (vinyl alcohol)‐based composite systems. J Appl Polym Sci 59: 655.
- Elliot SR (1978) Temperature dependence of ac conductivity of chalcogenide glasses. Philos Mag B 37(5): 553-560.
- Elliot SR (1987) Adv Phys 36:135.
- Mott NF, Davis EA (1979) Electronic Processes in Non‐Crystalline Materials Clarendon‐Press. Oxford, England.
- Long AR (1982) Frequency-dependent loss in amorphous semiconductors. Adv Phys 31(5): 553-637.
- Krimi M, Karoui K, Joseph SJ, Ben RA (2018) Phase transition, impedance spectroscopy and conduction mechanism of Li5Na0.5WO4. Physica E: Low-dimensional Systems and Nanostructures 102: 137-145.
- Elliot SR (1987) Frequency-dependent conductivity in ionically and electronically conducting amorphous solids. Adv Phys 36: 135.
- Mathlouthi S, Oueslati A, Louati B (2019) Vibrational analysis and conduction models in cesium gadolinium pyrophosphate compounds. Alloys and compounds 794: 417-424.
- Chaudhuri BK, Chaudhuri K, Som KK (1989) Concentration and frequency dependences of AC conductivity and dielectric constant of iron-bismuth oxide glasses-II. J Phys Chem Solids 50: 1149.
- Bergman R (2000) General susceptibility functions for relaxations in disordered systems. J Appl Phys 88: 1356-1365.
- Coondooa I, Panwarb N, Rafiqa M, Pulid V, Rafiq M, et al. (2014) Structural, dielectric and impedance spectroscopy studies in (Bi 90R0.10) Fe0.95Sc0.05O3 [R=La, Nd] ceramics. Ceramics International 40(7): 9895-9902.
- Schutt HJ (1994) A new phenomenological description of the electrical relaxation in ionic conductors. Solid State Ion 72: 86-88.
- Cole KS, Cole RH (1941) Dispersion and absorption in dielectrics I. Alternating current characteristics. J Chem Phys 9: 341-351.
- Enneffati M, Maaloul NK, Louati B, Guidara K, Khirouni K (2017) Synthesis, vibrational and UV–visible studies of sodium cadmium orthophosphate. Opt Quantum Electron 49: 331.
- Ajmi A, Karoui K, Khirouni K, Ben Rhaiem A (2019) Optical and dielectric properties of NaCoPO4 in the three phases α, β and γ. RSC Adv 9: 14772 .
- Gagandeep, Singh K, Lark BS, Sahota HS (2000) Attenuation measurements in solutions of some carbohydrates. Nuclear Science and Engineering 134: 208-217.
- Moh, Davis E (1979) (2nd edn), Oxford University Press, UK.
- Tauc J, Menth A (1972) States in the gap. Journal of Non-Crystalline Solids 8-10: 569-585.
- Barhoumi A, Leroy G, Duponchel B, Gest J, Yang , et al. (2015) Aluminum doped ZnO thin films deposited by direct current sputtering: structural and optical properties. Superlattices and Microstructures 82:483-498.
© 2020 Karoui K. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






