Dislocation Dragging Mechanisms and Long- Term Strength of Metal Crystals

Today and even more so in the future, microyield/creep in shear appears to be one of the fundamental material properties and key factors limiting service conditions for a new generation of metal alloys [1-4]. The increasing dynamical application of solution-hardened alloys as cost-effective structural materials stimulates extensive research to reveal the rate-controlling mechanisms responsible for improving their pre-yield (creep) resistance and long-term strength below macroscopic yield stress [4-6]. Nevertheless, over the years, research works under review [7-9] have been mainly performed to study the macroscopic variations in strain for a better understanding of the serrated yielding as a macroscopic phenomenon arising from the dislocation-solute interaction by a long-range diffusioncontrolled mechanism. This type of discontinuous and repeated yielding commonly referred to as the Portevin-Le Chatelier (PLC) effect is attributed to dynamic strain aging (DSA), in which the isolated solute atoms interact with mobile dislocations during straining. However, up to now, there is no evidence of a relationship between PLC banding and shear banding [9,10]. According to Cottrell concept [11], the DSA effect has firstly been associated with the dragging stress being caused by the formation of dense solute atmospheres around moving edge dislocations at the same velocity of alloy constituents. DSA in solid solutions is described as the diffusion of solutes to mobile dislocations temporarily arrested at obstacles [8]. It was suggested that a PLC effect expected from solute atmosphere dragging [12] arises from the dynamically unstable region with the jerky flow and serrated yielding subsequent to its formation. Following Cottrell’s concept of jerky flow, the thermally activated process of serrated yielding should occur with the activation energy (a.e.) for solute migration towards dislocations by a diffusion-controlled mechanism. In contrast, the a.e. of the PLC effect which controls the appearance of the serrations is comparable to vacancy migration energy, while the a.e. which governs the disappearance of the phenomenon is similar to self-diffusion energy [7].

There have been several attempts [13-15] to modify the Cottrell concept and to ascertain a DSA effect and jerky flow origin but neither of them fails to explain quantitatively the rapidity of the hardening in metals with decreasing temperature. Besides, much of on-going theoretical models describe the related PLC and DSA effects at long-term loads close to or above macroscopic yield without respect to the observed short-range interaction of point defects [15-18]. Much as these works have contributed to the elucidation of this problem but our knowledge of it is still far from being complete. At last, there is a long-standing argument that macroscopic changes in strain are accompanied by the multiplication of dislocations so that the thermoactivation (numerical) analysis is certain to become impossible by reason of the fine structural variations.

It has been until very recently that the basic assumptions of the Cottrell theory [11] have been seriously called in question [19,20]. The dislocation atmospheres forming and the bound dislocations dragging are considered to occur during microyield at stresses dτ/dυD>0 while the PLC effect arises during plastic instability at dτ/dυD<0 [17,21], i.e. achievement of critical dislocation rate υcr at their density appears to be critical condition for appearance of the effect associated with discontinuous pinning of dislocations [7]. This is a starting advance as compared to the classical concept which was current two or three decades ago. Nevertheless, nearly all previous studies on the interaction between dislocations and solutes have been limited to investigations of the long-term diffusion-controlled mechanisms. With this provision, despite considerable research efforts in the past the main source of the rapid increase in solid solution strengthening is still a matter of controversy. In any case, current theories do not appear to account for the observed dislocation microyield/creep resistance leading to an increase in long-term strength. The rate of rapid solid solution strengthening in hcp metal crystals, e.g. α-Ti at elevated temperatures [22] is associated with short-range mechanism rate-controlling the thermally activated overcoming of solute interstitials by dislocations (on the first order prisma planes). The activation process of the short-range mechanism is thought to occur in the dislocation stress field at less than atomic spacings (~0.1nm) without long-range diffusion and to enable the elastic energy of a system to be reduced. Thus, there are many questions that remain unanswered in the known approaches to dislocation dynamics problems where other mechanisms will clearly need to be considered.

Since there is little information in the literature on the theoretical dislocation long-term strength of solution- hardened alloys below macroscopic yield stress it, therefore, seems appropriate to indicate the possibility for continued work along these lines. The main purpose of the present study is to develop a physical theory for useful long-term strength excluding the premature fracturing of solution-hardened alloys below the macroscopic yield stress. The research aims at a better understanding of the basic principles of dislocation creep resistance responsible for the increase in the long-term strength of metal crystals. To provide further indepth insight into the physical origin of dragging effects the ongoing study focuses on the theoretical analysis of the dislocation calculations design based on physical modeling and activation of the most probable (short-range) mechanisms in order to identify them in the so-called multi-level solute defect structure enriched by substitutional solutes and strain-produced excess vacancies. Besides, this article evaluates the current understanding of relationships between microstructural parameters, dislocation pre-yield resistance and long-term properties of some promising metal alloy systems. From this view, it would be appropriate to clarify the subject of the pinning effects in rapid-hardening alloys and to reveal short-range rate-controlling mechanisms acting in the selected metal alloy systems. It is likewise the intention of the study to subject the measurements to a complete analysis

Our strength design relates to the edge dislocation theory for micro yielding where the dislocation sources operate prior to macroscopic yield stress. There has been a great deal of interest in accurately describing the short-range interactions between dislocations and excess vacancies, the density of which exceeds that of thermally equilibrium ones by several orders of magnitude [2,6]. Since thermally activated processes of dislocation microyield/creep and dislocation relaxation are controlled the same mechanism responsible for the strain rate, the dislocation relaxation will be considered as a creep at variable stress. This enables the thermoactivation (numerical) analysis of available data to be carried out at an unchanged dislocation structure for modeling and testing as well as permits a single activation process to be extracted from a more complicated pattern. Based on these simulations, analytical rate-equations were derived in order to reveal the rate-controlling dragging mechanisms responsible for the increase in dislocation creep resistance and long-term strength. Constant structure steady-state creep tests were performed to evaluate the a.e. and activation volume (a.v.) for selected solutionhardened alloys in the most promising hcp Mg-Al-Ca system and to compare them with those in the fcc Fe-Ni-C system under the loading conditions of interest in this study.

A rate-controlling model for the resistance to microyield/creep strain is proposed to describe the short-range dragging effects to be recognized. The higher probability W1,2 of the successful thermally activated jump for a dislocation in the force direction during passive dislocation relaxation or dislocation creep resistance can be calculated from the relation

where is the average velocity of a dislocation during dragging; α-the proportional coefficient dependent on the obstacle nature and dislocation parameters ; ν -the attempt frequency of the successful jumps for a dislocation; −λ -the activation distance between short-range obstacles where a dislocation is delayed during the waiting time

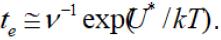
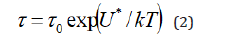
where τ₀ is a frequency factor dependent on lowering a potential barrier; U*-the a.e. needed for overcoming a thermally activated obstacle by a short-range mechanism. The relation (3) for an atom in the field of dislocation is different from well-known relation (2) by an amount of the binding energy E_b

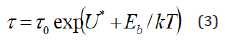
were E_b is the binding energy of a solute atom, (a paired defect or an associate) with a dislocation.

A little manipulation of equations (1) and (3) yields a dragging effect, if a single activation process controls the microyield/creep resistance and the number of places where the strain per successful fluctuation can take place. The rigorous description of the stressinduced dragging effect in terms of dislocation physics leads two types of the differential kinetic rate-equations which represent the related phenomena such as dislocation dragging during incipient pre-yielding and pre-yield (dislocation) relaxation.

In the 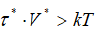pre-yield range, i.e. at higher stresses and elevated temperatures, there is no breaking off a dislocation from its atmosphere due to strong binding energy E_b between them. By reason of enough pinning of dislocations, the height of potential barrier U* increases by the value of E_b, i.e. U*+E_b with a fraction of the line defects proportional to exp(E_b/kT). Then for describing thermally activated dynamical dragging by the dislocation atmospheres, the equation for the shear micro strain rate can be reduced to the following form

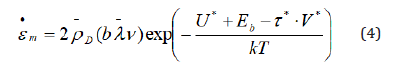
where •ε is equated to is the average mobile dislocation atmospheres density; b-the Burger′s vector; 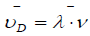the velocity of dislocation atmosphere dragging; 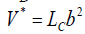the activation nano volume; LC-the activation length of mobile dislocation nano segment between mobile nodes of pinning; 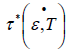the thermal component of applied stress.

In 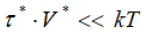the pre-yield range, i.e. at lower stresses and higher temperatures, in crystals containing solute atoms of low pinning strength [23], the binding energy E_b makes it possible the jump-like movement of dislocation to be typical for the onset of jerky flow by strain to first jerk. Therefore, the energy-level of ground state for the potential barrier U might be split up into two energy-level substates with the increased a.e. of U^*+E_b>U and a fraction proportional to exp(E_b/kT) for the dislocations being pinned as well as with the decreased a.e. of (U^*-E_b)<U and a fraction proportional to exp(-E_b/kT) for the mobile dislocations being unpinned. In other words, the height of potential barrier U changes by the magnitude of E_b, i.e. fluctuates within ±E_b. Hence, exp(E_b/kT) reproduces the attractive part of potential energy, while exp(-E_b/kT)-its repulsive part, e.g. detachment of dislocation from isolated atoms, paired defects or their complexes.

The motion of dislocation in its slip plane is, in general, a discontinuous process [8], so that there are reasons to believe that the short-range dislocation dragging in the onset of jerky flow is expected to be consistent with the well-known Le Chatelier-Braun physical-chemical principle of shifting the mobile equilibrium. Then the dynamical dragging by the repeated pinning of dislocations will be satisfied the equation for micro strain rate a

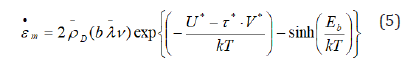
The original idea for dislocation analysis is that the thermally activated energetic level is split into two sublevels of the shortrange potential obstacle due to the discontinuous (repeated, positive and negative) increment of internal stress ±Δτ*. The latter arises out due to the two dragging forces needed for the thermally activated depinning and repeated thermally activated pinning of dislocations [24] to satisfy the Eq. (5) and to the Le Chatelier-Braun principle. 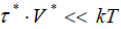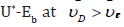From the physical point of view, over the range splitting of the energetic potential means its growth U*+Eb at and its decrease Thus, the binding energy Eb is one of the important parameters controlling dislocation creep resistance in the solid solution systems with mobile defect structure.

At higher stresses and elevated temperatures (τ*·V*>kT) the dislocation creep resistance for a given magnesium alloy in the Mg-Al-Ca-Ti system is found to be essentially governed by a ratecontrolling mechanism operating with the a.e. of 0.80±0.02eV or 1.28x10-19J for excess vacancy migration in the stress field of dislocation atmospheres (Figure 1). In addition, the value is in agreement with those estimated for some alloy crystals [8,23,25,26] and constitutes roughly one-third of that for selfdiffusion (2.08…2.24x10-19J). Snoek locking [27] is believed to be the stress-induced ordering mechanism operating in these alloys with a high rapidity due to the migration of excess vacancies to form solutes atmosphere around moving dislocations. Strong pinning of dislocations should be expected when locally bounded matrix atoms find themselves part of a passing dislocation [25]. Aging is as being caused by the movement of the vacancy around immobile solutes and as a sequence by the rotation of solute-excess vacancy pairs to form the segregations around moving dislocations [12]. The rateequation (4) confirms the rapid nature of short-range interaction between the dislocations and solutes in solid solutions enriched by excess vacancies. According to the analytical estimations of rapid kinetics in the τ*·V*>kT range the dislocation atmospheres are certain to generate in magnesium alloys the strain-produced excess vacancies.

At lower stresses and higher temperatures (τ*·V*<< kT) the dislocation creep resistance is assumed to be controlled by a dragging mechanism operating with the a.e. of 0.50±0.02eV or 0.85x10-19J for migration of excess vacancy/solute paired complexes in the stress field around mobile dislocations. Its reliable value yielded by the solution of the Eq. (5) is significantly lower than that for self-diffusion (1.35eV) and lower than that for isolated vacancy formation (0.8eV) and diffusion of any alloying element, i.e. another most probable dislocation mechanism is ratecontrolling. As fast as an atmosphere consisting of the complexes is formed around a dislocation, the activation short-range ordering mechanism in the stress field of dislocations the enables dragging effect to be enhanced much more compared to single solute atoms. Taking into account that the unlocking of pinned dislocations and the motion of unpinned dislocations are controlled by the same thermally activated mechanism [27,28] the thermally activated slip dragging by the excess vacancy/solute complexes having a high rapidity of the short-range pinning is believed to be the most likely rate-controlling dragging mechanism responsible for the pre-yield resistance.

Figure 1: Activation volume V* as a function of applied stress thermal component τ* (a) for a dislocated solid solution in hcp Mg-12.5Al-1.3Ca system (1, 2, 3) compared with that of the fcc Fe-32Ni-0.1C system (4): 1-dynamical dragging of mobile dislocations by solute-excess vacancy atmospheres with the a.e. of 0.8 at 423K evaluated by Eq. (4); 2-discontinuous (repeated) pinning of dislocations in early stage of jerky flow conditions with the a.e. of 0.5eV at 523K evaluated by Eq. (5); 3-dynamical dragging of dislocation by solute atmospheres under jerky flow for Fe-32Ni-0.12C alloy [23]; variations of activation volume V* with the activation length of mobile dislocation nano segment LC (b). Here υss ν =1010Hz; b=3.2 x 10-10m; Eb= 0.3 eV, kT=0.036 eV at 423K and 0.045 eV at 523K; • 0 ε =10.24 s-1; LC= 6.0nm (for V*=20b3), LC=10.8nm (for V*=36b3).

Stress relaxation is determined by the following relation Ref. [27]

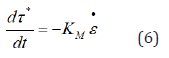
Where, t is the relaxation time for applied stress; KM is the elastic rigidity in tension to be constant at any test conditions. For the thermally activated dislocation mechanisms of dragging by solute atmospheres at τ*∙V*>kT, the parameters of relaxation can be determined as follows. By combining Eqs. (1), (4), and (6) one can obtain the differential relaxation equation (7) of the form

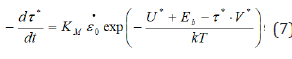
We omit here some intermediate computations involving the mathematical treatment of Eq. (7) by the combined operations of separating the variables, and setting up the relevant integral equation to meet conditions τ*(t)=τ*_max at t=0 and τ*(t)=τG (final time of relaxation). Then this relaxation equation was integrated and found the logarithm. After a little manipulation, the expression obtained was re-arranged as the equation of dislocation relaxation which can be described by the expression

where 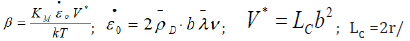C₀·exp(-Eb/kT); LC is the length of dislocation nanosegment between mobile nodes of pinning; r-radius of curvature for a dislocation (r=Gb/τ*); C₀-initial concentration of solutes.

Taking the antilogarithm of Eq. (8) we get the modified equation for the relaxation time

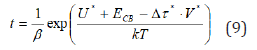
In going from thermal to a thermal component τG (at τ * ≅ 0 ) the Eq. (8) of stress relaxation reduces to the second-kind equation of relaxation

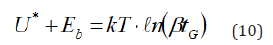
By analogy with the above-mentioned procedure, the stress relaxation equations can also be deduced

for the discontinuous (repeated) pinning of dislocations in the τ*∙V*<< kT range. For the case, the course of calculations is almost the same as that obtained for the τ*∙V*>kT. Then the dynamic dragging of mobile dislocations is described by the relation

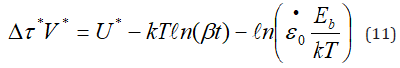
The present stress relaxation analysis is found to fit generally into semi-logarithmic relationships obtained previously by [29,30]. Nevertheless, numerical analysis of the equations in the early models of relaxation [29-31] is absent which makes it difficult to examine their reliability and justification for their analytical solutions. At the same time all the terms in our newly developed equations of stress (dislocation) relaxation have physical meanings.

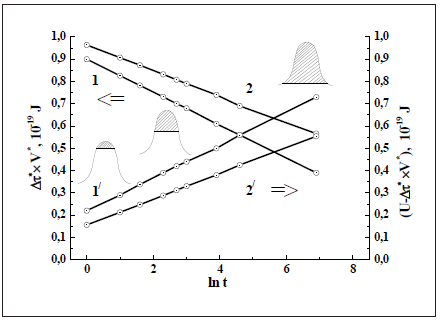
A pronounced solid solution strengthening effect is attributed to the large long-range stress fields due to a thermal stresses τG, while the relative strength of the short-range obstacles produced by solutes is not so obvious. The energy of dislocation, when unaided, is insufficient to pass a tetragonal (paired) defect as a short-range barrier. The extra energy to overcome it must be supplied by thermal fluctuations. The present theory enables the net a.e. needed for overcoming the height of short-range barrier potential to be resolved into two time-dependent constituents associated with the partial a.e. for power (elastic) interaction between alloy ingredients, and the partial a.e. for long-term thermal vibrations of a lattice (Figure 2). The observed logarithmic plot of stress (dislocation) relaxation at each temperature is certain to consist of the two linear segments separating the data into thermal and power (elastic) energetic contributions. The two energy-sharing components acting at atomic distances (~0.1nm) may be exemplified by two energy terms: (i) the first term Δτ*∙V* is due to the work done by the drag stress component τ* and (ii) the second term U-Δτ*∙V* in Eqs. (4) and (5) should be considered as energy of thermal vibrations for a crystal lattice. Thermal energy as a driving force equal to the shaded area on the diagram will move dislocation on a shortrange distance by the energy of atomic thermal fluctuations linked to the crystal lattice vibrations. The idea of separating the timedependent contributions concerning the thermal and mechanical breaking of dislocation is consistent with the concept of thermally activated dislocation depinning by [24]. Numerical analysis of the dislocation relaxation following Eqs. (8) and (11) shows that the power component τ* decreases linearly with loading time and tries to be as high as the a thermal component τG (at τ*=>0), while the energy when supplied to the short-range obstacle by long-term thermal fluctuations, on the contrary, increases linearly with time up to the value of resistance to the dislocation motion. The ordering forces exerted by a stress field around dislocation are opposed by the disordering forces of lattice thermal vibrations [23], the thermal energy of which tends to randomize a solute distribution. The growing contribution of thermal activation energy (Figure 2) signifies the increase in the time-dependent strain produced by successful thermal fluctuations. This theoretical calculation is a good test for the physical sense of the model proposed.

Figure 2: Numerical analysis of the dislocation relaxation for HCP Mg-12.5Al-1.3Ca0.1Ti alloy with separating the time-dependent contributions of the power Δτ*∙V*, (1 and 2) and thermal U-Δτ*∙V*, (1′ and 2′) components to the net activation energy for overcoming a short-range potential obstacle by a dislocation at 523K (1 and 1′) using Eq. (11) and 423K (2 and 2′) using Eq. (8) in nano volumes 36 b3 and 20 b3, respectively. Here U is the full free (available) energy for thermally activated overcoming the short-range obstacle; KM=4 x 106 J/m2; G=17 GPa; μ=0.35.

Principles of effective alloying have been quite successful in the past in developing alloys for high-temperature service aerospace applications. Following concept [1] a measure of “maximum usefulness temperature” during straining is arbitrarily defined as the temperature at which the alloy can withstand the stress of about 69MPa for 100 hours without fracturing. This qualitative criterion allows evaluating the alloy-efficiency for pure metals. Over the past several years, in applied physics successfully advanced in terms of preceding dislocation theory, on the whole, a new theoretical-cognitive situation has shaped which requires the development of more accurate (quantitative) criteria for further improving physico-mechanical properties of metal crystals below the macroscopic yield stress [3,10,19,32]. Following the situation, it is much appropriate to develop a diagnostic approach that provides for the opportunity of predicting and preventing the harmful and dangerous defects in solution-hardened metal alloys for their safe long-term exploitation in machinery. A little manipulation yields energy balance for the steady-state of dislocation creep s = ⋅ t •ε ε and for the characteristic time t* to achieve a measured quantity of useful (uniform) strain before a localized shear, 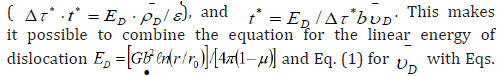and Eq. (1) for − D υ with Eqs. (4) for strain rate For the case, the general ultimate transition to the elastic instability should be replaced with a newly developed dislocation criterion of instability for a defect structure as

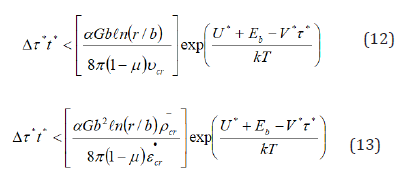
With this provision, at T→T_s *, and τ*→0

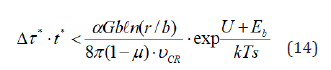
Here Δτ * is the threshold dragging stress, under which a transition from uniform strain to localized shear is the most likely to occur at ( ) D T cr − − υ τ * , >υ ; α-Schmidt factor; μ-Poisson’s ratio; Gb-the elastic shear stability (rigidity) of crystalline lattice; αGb2=f (τ*, T)-the linear tension (excess energy) of a dislocation with the a.e. of about 0.2 Gb3; υcr (T, τ*)=λ∙ν-the threshold dislocation velocity corresponding to the measured strain rate •ε ; -the density of dislocations; -the threshold strain rate; us Τ -the useful temperature by [1]; Ts-the entropic temperature, under which thermal fluctuation are capable to overcome a shortrange potential obstacle without stress (τ*=0). According to the criterion, the threshold stress of dragging is related directly with the elastic shear stability of a crystal lattice, strain rate, density, excess energy and velocity of dislocations as well as strength of interatomic bonds (through E/G modulus). Interconnection of the subcritical parameters ( • − − D D ε ,υ ,ρ ) with various rigidity, i.e. the shear stability of crystal lattice (αG) and linear tension (excess energy) of dislocations (αGb2) enables to predict the attainment of the dislocation strength at short-range distances. The analytical equations (12-14) with the same structure furnish a consistent criterion of the useful long-term strength connecting the threshold stress Δτ* with properties of the crystalline lattice, elastic fields of mobile dislocations as well as with the activation parameters that reveal the nature of a most probable rate-controlling mechanism. Besides, the energy (dislocation, quantitative) criterion describes a subcritical transition from the uniform elongation through a uniformly dense dislocation distribution to the concentrated slipping and localized shear responsible for the loss of the shear elastic stability for crystal lattice and, as a sequence, microplastic (dislocation) instability.

At low strain rates dragging stress in steady-state increases almost linearly with the dislocation velocity D −υ only in the early stage of the solute atmosphere formation. According to the inequality (12) at * / < 0 − dτ dυ D the dragging stress is expected to increase with decreasing the dislocation velocity D −υ , when it exceeds the critical value by a Cottrell solute diffusioncontrolled (long-term) mechanism [12,33]. Delay time is inversely proportional to the dislocation velocity (~1/υD) and has a maximum at a critical dislocation velocity υD and hence for strain rate • 0 ε according to Eqs. (12) and (13). In this case, after passing through a maximum at and const D = −ρ due to a partial unlocking of rapid dislocations, the system in the stable state turns into dynamically unstable plasticity state in the region with rapid dislocation sliding. The theoretical results obtained for dislocation velocities by inequality (12) fitting a measured strain rate •ε <εcr by the inequality (13) are in a good agreement with modeling study and theoretical calculation of critical dragging maximum observed [12]. The validity of the present dislocation criterion was experimentally verified using a strain-rate change test which has been described in detail elsewhere [24,34]. The creep rates •εcalculated with Eqs. (4) and (5) and compared with experimental data are summarized in Table. It is noteworthy that the contribution of the short-range thermally activated mechanisms to the dislocation microyield/ creep resistance is thought to be enhanced with slowing strain rate (dislocation velocity). The newly developed magnesium alloy in the hcp Mg-Al-Ca system is found to have the best combination of short-term and long-term properties compared with commercial alloy AZ91D.

A possibility for solute atoms to interact with a dislocation if the time is too short to activate the long-range diffusion-controlled mechanism was first suggested [33] and analyzed [34]. The most striking advance in the understanding of the rapid interaction of individual solute atoms with individual mobile dislocations was achieved [35]. Nevertheless, despite considerable research efforts in the past, in any event, current theories fail to explain with the present evidence the observed rapid kinetics of hardening in solid solutions as well as the deviation of the fundamental equation for short-range order strengthening from experimental data [36]. Some good work is underway along these lines, but original diffusion rate-equations can lead to serious discrepancies since the kinetic parameters are no longer consistent with the values taken from the diffusion data. The correctness of such an interpretation is based on several grounds. Firstly, a dragging effect is related to the direct solute-dislocation interaction with binding energy Eb rather than to the mobility D/kT by the Einstein relation, i.e. diffusion drift velocity [17]. Unlike the theoretical aspects of macroscopic changes of diffusivity D describing in the form of diffusion drift the macroscopic flows of substance, the binding energy Eb gives a result of short-range interaction at atomic distances. Secondly, since the diffusion is not necessary constituent or integral part of high-temperature creep [37], it is difficult yet to calculate the diffusion process numerically due to the vacancy mechanism which needs many unknown quantities. Only a few theoretical approaches to this problem have been advanced in the literature. To illustrate, according to Sherby with co-workers [18], the atom mobility and elastic modulus compensated stress σ / E are believed to be two principal factors influencing the creep strain rate ( •ε ) at a given stress. Nevertheless, although at the same diffussion mobility of solutes the excellent correlation between and σ/E has been observed in many metal alloy systems, in the suggested rateequations [18] relevant to the problem a term f (σ / E) is yet unspecified function.

Unlike the Cottrell atmosphere, the ordered Snoek atmosphere is formed in the effective stress field of dislocations by a shortrange ordering mechanism [28,36], which causes the dragging force for dislocations moving against the energy gradient depending upon their velocity. Since Snoek short-range ordering precedes the Cottrell mechanism of the solute atmosphere formation, the subcritical value of dislocation velocity D υ is attained for highpurity α-Fe crystals at •ε of 10-8s-1 even at r.t. [28]. This result is in reasonable agreement with the calculated values of D υ for high-purity magnesium alloy crystals under examination at the same dislocation density (Table 1). The Snoek-type dislocation atmosphere is believed to be formed as the complex consisting of an excess vacancy and a solute alloying element. The idea for a local loss of the crystalline lattice stability near-linear defects was first advanced [37] for vacancy clusters and complexes of points defects having elastic distortions around them. With that, the achievement of critical parameters for the store internal energy, e.g., the local critical density of dislocations during time-dependent strain is thought to be caused by deformation instability, first of all, by reason of loss of shear stability of a dislocated crystalline lattice and localized shear below the macroscopic yield stress. These effects are accompanied by decreasing microyield/creep resistance and long-term strength.

Table 1: Micromechanical properties of conventional and newly developed experimental magnesium alloys at 423K

Table abbreviations: r.t: Room Temperature; h: Hours; Exp: Experiment

The appearance of the relaxation spectra of internal friction in hcp magnesium alloy indicates that solute atoms are expected to be paired with excess (strain-produced) vacancies, which attract them strongly producing large (tetragonal) lattice distortions [2,6,33]. With this provision, the vacancies will remain in the solution being associated with the solutes. The solute/excess vacancy complexes are actually elastic dipoles with different binding energy. Published data and experimental evidence reported in the periodic literature [24,38] strongly support our identification of the dragging mechanisms proposed. For example, under the data by [23] the a.e. has been estimated as being the a.e. for vacancy migration (approximately 0.9eV in the fcc Fe-Ni-C system). However, the theoretical values of the a.e. for the vacancy migration (0.65eV for FCC Al) are essentially higher than those obtained from experimental data in the Al-Mg system (0.45eV) due to the formation of a vacancy/solute complexes with binding energy E_b~0.2eV [38].

According to the kinetics of DSA [23] the observed rapid jerky flow on the serrated stress-strain curves can be explained on the basis of the stress-induced short-range ordering mechanism [27,28] rather than Cottrell elastic approximation or Suzuki chemical dislocation pinning mechanism. The rate-equation (5) in subsection 3.1 for repeated pinning of dislocations evaluates the extent of smoothening curves of plastic strain at the initial stage when occurring the first plastic deformation jerks in preceding jerky flow. As a matter of fact, jump-like (discontinuous, repeated) pinning of moving dislocations is likely to facilitate rather than to cause the proceeding of jerky flow or DSA. By reason of its general sense, the magnitude of initial jerks in the form of stress drag increment and abrupt fall in load can be regarded as indicative of the stress differential between the breakdown stress at which dislocations escape from their atmospheres and the stress at which they move easily through the lattice before being pinned again [16]. It is reasonable to assume that in the τ*∙V*<< kT range the dragging effects under examination are typical for the onset of jerky flow by strain to a first deformation jerk the jerkiness effect relates to mesoscopic phenomena to occur below the macroscopic yield stress, our system of the newly developed rate-equations can be expected to give a good result for describing the onset of jerky flow.

The basic conclusions could be drawn from the results obtained and may be stated as follows:
1. A physical theory of useful long-term strength based on mathematical modeling of the thermally activated (short-range) resistance to dislocation movement and on the Le Chatelier-Braun’s physical-chemical principle of shifting the mobile equilibrium has been evolved for adequate describing solid solutions enriched by excess vacancies and their rapidly-hardened alloys with hcp and fcc structure. The theory furnishes an explanation of the above dragging effects in the early stage of their formation including the onset of atom ordering and describes the direct interaction between defects and solutes involving the jump-like movement of dislocations with increasing temperature. This makes it possible to separate the time-dependent contributions of power and thermal components to the net activation energy needed for overcoming the short-range obstacles.
2. Judging the results obtained, at least two underlying types of the dislocation dragging mechanisms were identified by using a new model-based analytical rate-equations when evaluating the activation energies intrinsic to creep-resistant alloys in the hcp Mg- Al-Ca, Ti and fcc Fe-Ni-C systems. At higher stresses and elevated temperatures (τ*∙V*>kT) the movement of glide dislocations is most likely to occur jointly with their solute atmospheres so that for the case, the dynamic dragging of micro yielding is provided by the resistance of mobile dislocation atmospheres with the a.e. for vacancy migration. At lower stresses and higher temperatures (τ*∙V*<< kT) the dynamical dragging of creep strain is believed to be due to the constant ( discontinuous, repeated) interactions between mobile free dislocations and solutes by a jump-like mechanism. For the case, a point peculiar interest is an enhanced effect of dragging in the early stage of the jerky flow. It may be appropriate for improving the long-term strength of high-temperature alloys.
3. Over the time-dependent microyield/creep range, theoretical simulations and experimental evidence predict a potentially useful measure of long-term strength formed in the stress fields of mobile dislocations. The quantitative (dislocation) criterion of useful long-term strength is proposed for quantitative assessment of the alloying effectiveness as to the best possible metal alloy crystals with minimum strain location. The criterion describes material conditions that prevent a transition from uniform strain to localized shear leading to the elastic and microplastic instability of a dislocated crystal lattice. The present theory suggests that the transition state might be considered as being the physical restriction in dislocation long-term strength. In the context, a threshold dragging stress as a function of uniform strain resistance is directly related to elastic (shear) stability of a dislocated crystalline lattice, line tension (excess energy), velocity and density of sliding dislocations.
4. The findings obtained are in reasonable agreement with strain rate change and stress relaxation measurements, test findings and isothermal observations, which are suggestive of the cluster-like complexes. In summary, therefore, the present theoretical study will hopefully stimulate further experimental investigations that could lend a better understanding of the mechanisms responsible for the formation of dislocation creep resistance and long-term strength in metal crystals. The present newly developed diagnostic approach is believed to provide a physical basis not only for a proper understanding of dragging effects but also for alloy development. The proposed method can be expected to be appropriate in describing the creep behavior of metal alloy systems as a starting point for further development of the rapid-hardening and creep-resistant alloys with a minimum of localized shear effects.

The author is indebted to Prof. V.A. Tatarenko and Prof. B.A. Movchan for communicating some of the theoretical results prior to their publication. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. The author declares no conflict of interest.

1. Abraschian R, Abraschian L, Robert E (2009) Physical metallurgy principles (4^th edn), Cengage Learning, Stanford, USA.
2. Tkachenko VG (2009) Contemporary trends of the development of physics of light metals. Progress in Physics of Metal 10(1): 103-130.
3. Kassner ME (2015) Fundamentals of creep in metals and alloys (3^rd edn), Elsevier-Verlag, Butterworth-Heinemann, UK.
4. Tkachenko VG, Maksimchuk IN, Volosevich P, Lashuk NK, Malka AN (2006) Creep resistance and long-term strength of structural magnesium alloys. High Temperature Materials and Processes 25(1-2): 97.
5. Pekguleryuz MO, Kaya AA (2003) Creep resistant magnesium alloys for powertrain applications. Advanced Engineering Materials 5: 74-93.
6. Tkachenko VG, Kim KH, Moon BG, Vovchok AS (2011) Design and microstructural analysis of magnesium alloys for dynamical applications. Journal of Materials Science 46: 4880-4895.
7. Dinhut JF, Bonou T, Moine P (1976) Phenomene portevin-le-chatelier in ordered and disordered Fe-Co alloys. Acta Metallurgica 24(5): 445-451.
8. Van den Beukel A (1975) Theory of the effect of dynamic strain aging on mechanical properties. Physica Status Solidi 30(1): 197-206.
9. Mesarovich D (1995) Dynamic strain aging and plastic instabilities. Journal of Mechanics and Physics of Solids 43(5): 671-700.
10. Fressengeas C, Beaudoin AE, Lebyodkin M, kubin LP, Estrin Y (2005) Dynamic strain ageing: A coupled dislocation-solute dynamic model. Material Science Engineering: A 400-401: 226-230.
11. Cottrell AH (1953) Dislocations and plastic flow in crystals. Oxford University Press 119(3095): 551.
12. Yoshinaga H, Morozumi S (1971) The solute atmosphere round a moving dislocation and its dragging stress. Phil Mag A 23(186): 1351-1385.
13. Leyson GPM, Hector LG, Curtin WA (2012) Solute strengthening from first principles and application to aluminium alloy. Acta Materialia 60(9): 3873-3884.
14. Sills RB, Cai W (2016) Solute drag on perfect and extended dislocation. Phil Mag 96(10): 895-921.
15. McCormick PG (1988) Theory of flow localization due to dynamic strain aging. Acta Metallurgica 36(12): 3061-3067.
16. Hayes RW, Hayes WC (1982) On the mechanism of delayed discontinuous plastic flow in an age-hardened nickel alloy. Acta Metallurgica 30(7): 1295-1301.
17. Sakamoto M (1989) Diffusion equation and cottrell atmosphere dragging of edge dislocation in high concentration solid solution. Materials Transactions 30(5): 337-344.
18. Sherby OD, Klundt RH, Miller AK (1977) Flow stress and subgrain stability at elevated temperatures. Metallurgical Transactions A 8: 843-850.
19. Mandal PK (2016) Study of hardening mechanisms in aluminium alloys. Int Journal of Engineering Research and Applications 6(1): 91-97.
20. Zhang F, Curtin WA (2008) Atomistically-informed solutes drag in Al-Mg. Modelling Simul Sci in Mater Eng 16(5): 1-22.
21. Yoshinaga H, Morozumi S (1971) A portevin-le chatelier effect expected from solute atmosphere dragging. Phil Mag A 23(186): 1351-1366.
22. Conrad H (1967) Thermally activated deformation of α titanium below 0.4 T_M. Canadian Journal of Physics 45(2): 581-590.
23. Rose KSB, Glever SG (1966) A study of strain aging in austenite. Acta Metall 14: 1505-1516.
24. Saul RH, Bauer CL (1968) Thermally activated dislocation depinning in dilute copper alloys. J Appl Phys 39(3): 1469-1477.
25. Conrad H (1964) Thermally activated deformation of metals. Journal of Minerals 16(7): 582-588.
26. Beever CJ (1963) Electrical resistivity observations were quenched and cold-Worked magnesium resistivity electrical measurements on the magnesium hardening and cold deformed observations of electrical resistance year quenched, and magnesium cold worked. Acta Metall 11(9): 1029-1034.
27. Snoek JL (1941) Effects of small quantities of carbon and nitrogen on the elastic and plastic properties of iron. Physica 8(7): 711-733.
28. Schoeck G (1956) Moving dislocations and solute atoms. Phys Rev 102(6): 1458-1459.
29. Dotsenko VI (1973) Stress relaxation in crystals. Phys Stat Sol 93(1): 11-43.
30. Surgent GA (1965) Stress relaxation and thermal activation in niobium. Acta Metall 13(6): 663-671.
31. Kioussis NG, Ghoniem NM (2010) Modeling of dislocation interaction with solutes, nano-precipitates and interfaces: A multiscale challenge. J Computational and Theoretical Nanoscience 7: 1-30.
32. Regev M, Rasen A, Bamberger M (2001) Qualitative model for creep of AZ91D magnesium alloy. Metallurg Mater Trans 32(6): 1335-1345.
33. Taketomi S, Matsumoto R, Miyazaki N (2011) Atomistic study of the competitive relationship between edge dislocation motion and hydrogen diffusion in alpha iron. J Mater Res 26(10): 1269-1278.
34. Rubiolo GH, Bozzano PB (1995) Dynamic interaction of impurity atmospheres with moving dislocations during stress relaxation. Mater Trans 36(9): 1124-1133.
35. Fleisher RL (1985) High-temperature, high-strength materials-An overview. J Metals 37: 16-20.
36. Arsenault RJ (1966) An investigation of the mechanism of thermally activated deformation in Ta and Ta-base alloys. Acta Metall 14: 831-838.
37. Clapp PC (1970) A localized soft mode theory for martensite transformations. Phys Stat Sol 57(2): 561-569.
38. Mukherjee K, May T, D Antonio C, Maciag RJ (1979) Serrated yielding in a 5005 aluminium alloy. Met Trans 1(11): 3233-3234.