- Submissions

Full Text
Research & Development in Material Science
Links Between Mechanical Properties and Local Atomic Structures of Cu–Zr Bulk Metallic Glasses
Soyoung Jekal*
Paul Scherrer Institute, Switzerland
*Corresponding author: Soyoung Jekal, Condensed Matter Theory Group, Paul Scherrer Institute, CH-5232 Villigen PSI, Switzerland
Submission: November 08, 2019;Published: November 14, 2019

ISSN: 2576-8840 Volume 12 Issue 2
Abstract
Molecular dynamics simulations were carried out to investigate the influence of annealing process at glass transition temperature (Tg) on the atomic structure of a model Cu-Zr bulk metallic glass (BMG), especially icosahedral short- and medium-range orders (SRO and MRO). Analysis of SRO and MRO is done on voronoi tessellation, bond angle distribution and connectivity of clusters. It is found that the amount of icosahedral content of the system is significantly increased in a well relaxed structure. Since such SROs construct MROs via the icosahedral polyhedron connections, the size of MROs becomes larger as the annealing time is getting longer, and eventually make a huge cluster which can be considered as a rigid backbone. While we considered four connection types of vertex-, edge-, face-, and volume-sharing, the huge cluster in the relaxed samples mainly involve volume-type connection and exhibits a remarkable athermal plasticity that great stiffness and great yield strength compared to the as-quenched samples. In addition, the bond-angle distribution of annealed sample shows sharp peaks at specific bond angles which is an evidence of crystallized Laves-phase formed by icosahedral atoms, however the peaks are to be broaden after loading, which indicates decreasing amount of icosahedral content and their shape distortion. These results suggest that icosahedral content in a bulk metallic glasses plays a key role to determine the mechanical properties such as rigidity and maximum stress carrying capacity.
Introduction
Bulk metallic glasses (BMGs) have drawn much attention due to their interesting mechanical properties such as extraordinary elastic strain limits and a high tensile yield stress [1-6]. For example, their yield strengths can be up to 1 to 5GPa and elastic strain limits up to ~2% [7-10]. However, their use for engineering applications has been challenging since BMGs exhibit localized strain softening leading to failure and brittleness. The underlying atomicscale plastic mechanisms are believed to be mediated by a local microscopic mechanism [11-14]. Such localized processes have been observed during high-strain deformation atomistuc simulations [15-22] inspiring the development of the shear transformation zone (STZ) concept and the effective temperature theory of athermal glass plasticity [23-25].
Much work has been done to clarify the connection between the local atomic structure of a glass, its atomic- scale structural evolution and how this collectively results in its macroscopic mechanical properties. Early work by Chaudhari and Turnbull developed the idea that local glassy structure relaxes towards a maximal packing of local tetrahedral arrangement of atoms which in most cases results in minimizing the bond energy. The local packing of such unit structure could however only be achieved through distortion, resulting in the frustrated structure of the central atom’s icosahedral coordination. Later, Nelson and co-workers considered the amorphous solid in terms of an optimal packing of such icosahedral structures [26-28]. Because it not possible to pack icosahedral structures in a space-filling way, defected icosahedra are needed in which the central atom is either under- or over-coordinated. This introduced the notion of local disclinations and a rudimentary (although mathematically robust) theory of defects for glassy systems [26-28]. The picture which therefore emerges is that the transition to the glassy state is structurally characterized by an increase in the number of local atomic environments with an approximate icosahedral coordination, and that the material’s extreme rigidity (high stress-strain range to failure) is related to the topological nature of the disclination content-locally frustrated icosahedral structures and their connectivity.
The above considerations have been considered from the perspective of both short-range order (SRO-icosahedral environments), and medium range order (MRO-connectivity of icoshaedral environemnts) within the amorphous solid. Ma and co-workers employed the local polytope content to characterize the relationship be- tween the structure and the mechanical properties in CuZr amorphous systems with different atomic concentrations [29]. Here the local polytope associated with an atom is the polyhedron derived from a Voronoi tesselation of the atomic positions. They found that the polytope most sensitive to the structural state is the icosahedron of twelve coordinated Cu atoms. Icosahedral content therefore depended on the concentration of Cu [29,30]. How such SRO and MRO relates to the structural state has been a central topic in past atomistic simulations of model amorphous systems, with particular focus on the affect of athermal/ high-strain rate deformation and temperature [31-33] protocols. For example, in a Lennard-Jones model binary glass both the average cohesive energy and free volume scales linearly with icosahedral content [32] indicating a direct relationship with the enthalpy of the system [31]. The linear relation with energy has also been seen in material-specific MD using the embedded atom method (EAM) [34] suggesting a quite general connection that originates from a minimization of internal stresses rather than energy.
In the present study, we use the embedded-atom model (EAM) potential [35,36] which is particularly appropriate for metallic systems, and we select a typical binary Cu-Zr alloy which is able to form a bulk metallic glasses with a critical casting thickness of few millimeter due to a good glass-forming ability, experimentally [37]. To investigate an atomic fraction dependency, CuxZr100−x with x=50,64,75 are compared. We found Cu75Zr25 that sample with higher Cu fraction composes more icosahedra than Cu50Zr50 and Cu64Zr36. Furthermore, long annealing process at Tg creates the another significantly large amount of icosahedral content of the system. Via the connectivity of vertex-, edge-, face-, and volume sharing, such icosahedra construct the clusters, regarded as MROs. While the size of the cluster becomes larger as the annealing time is getting longer, a huge cluster is obtained in the most relaxed sample mainly involves volume type connection. In perspective of the mechanical properties such as the athermal plasticity and elasticity, the annealed samples which contain a huge size of cluster show greater yield strength, ultimate strength, and elastic stiffness than the as-cast sample. Moreover, the specific sharp peaks in a bondangle distribution, are to be broaden after loading, which indicates destruction of icosahedra content and their shape distortion.
Methodology
The MD simulation presently carried out use the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package [38]. Atomistic visualization and analysis is done with the OVITO visualization soft- ware. An EAM based empirical potential [35,36] is used to model the Cu Zn binary alloy system [39].
Sample preparationAmorphous Cux Zr100−x (x=50,64,75) samples, with a total number of 24’000 atoms, were prepared. Starting from a face centered cubic arrangement with a random chemical arrangement, samples were melted at 2000 K, which is above the melting point of the CuZr system and equilibrated for 10 ns using an NVT ensemble (fixed volume conditions). Temperature was controlled by a Nose-Hoover method [40]. Then, using an NPT ensemble (fixed zero pressure conditions) the samples were quenched to a temperature of 50K, using a cooling rate of 1.95 X 109K/s. We refer to these samples as “as- quenched”. Such a linear quench was also interrupted and held close to a glass transition below but close to the temperature regime at which the systems transits to the glassy state. For each sample (concentration) this was for chosen time periods up to 1000ns, after which the quench was continued down to a temperature of 50K. These samples are referred to as “annealed” samples.
Figure 1: (a) Cohesive energy and (b) Volume per atom as a function of decreasing temperature of Cu50Zr50, Cu64Zr36, and Cu75Zr25 samples containing 24’000 atoms. Opened and filled circles represent as-quenched and 1000ns annealed samples, respectively. The intersection of the gray linear fitting lines in the volume curve indicates the corresponding fictive glass transition temperature.

The variation of cohesive energy and atomic volume with respect to the temperature for a linear quench protocol is displayed in Figure 1. The opened circles and filled circles respectively represent the asquenched and annealed protocols. For the as-quenched protocol, the slope of the cohesive energy and volume versus temperature curve changes below ~1000K, which is a signature of a transition to the glassy state. The precise temperature regime at which this occurs will depend on the chosen cooling rate. The point where the slopes of the glassy and liquid-like lines intersect defines the fictive glass temperature, Tgfictive. For the annealed samples, the hightemperature simulations for 1000ns results in a significantly lower cohesive energy and atomic volume, for all chemical compositions considered.
AnalysisThe present work employs a number of well-known local atomic structural measures:
1. To determine the topological short-range order (SRO) of the generated atomic configurations, the Voronoi tessellation of the atomic coordinates was used. The Voronoi index (VI) is denoted as < n3, n4, n5, n6>, where ni corresponds to the number of i-edged polygons. An icosahedral environment would give a VI of <0,0,12,0> indicating that the local Voronoi-generated polyhedron. Such an analysis method has been used extensively in past works [31-34,41,42]. This analysis is done within the OVITO atomistic visualization software [43] which uses the Voro++ package.
2. To gain insight into the local connectivity of the icosahedral environments and therefore begin to probe MRO, the work of Lee et al. [44] is followed. This method investigates the number of shared neighbours between two nearest neighbour icosahedrally coordinated atom. If an atom contains more than one such nearest neighbour, the shortest bondlength nearest neighbour is taken. This allows the derived number of shared neighbours to be uniquely assigned to a particular atom. Five types of connectivity are labelled as vertex-type (sharing one atom), edge-type (sharing two atoms), face-type (sharing three atoms), and volume-type (sharing five atoms)-type connections. Those icosahedrally coordinated atoms without such nearest neighbour are labelled as no-connection. This approach will referred to as ICA-connectivity.
3. Another approach to investigate small clusters of nearest neighbour icosahedrally coordinated atoms and therefore the SRO/ MRO is via the bond-angle distribution between triplets of such atoms. The bond angle at atom i, due to nearby atoms j and k is calculated as
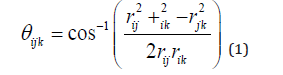
Where rij is the distance between two nearest neighbor atoms i and j. In the present work, nearest neighbour ICAs are defined to be within a distance of 2.6Å from each other. By investigating the bond- angle distribution of a model CuZr system, Zemp et al. [45] were able to identify CuZr super clusters formed by volume-type connections. The obtained distributions peaked at bond angles of 60˚, 120˚, and 180˚ suggesting small segments of the Laves crystal structure where present.
In addition to the above we introduce an explicit structural measure based on the bonds between nearest neighbour icosahedrally coordinated atoms. Motivated by the work of Chaudhari and Turnbull, and Nelson and coworkers [26-28], we assign to each such bond the number of shared neighbours. A value of n reflects the packing of n tetrahedrons (each defined by the two neighbouring ICAs and two common nearest neighbours which themselves are neighbours) around the bond. Following Refs. [26,27] a value of n=5 reflects a disclination-free bond whereas n=4/6 would represent a disclination a negative/positive character.
Results and Discussion
To investigate structural evolution during the employed temperature protocols, the percentage of icosahedrally coordinated atoms is calculated as a function of temperature. Figure 2 plots this data for both the as-quenched and annealed samples. For each temperature, thermal vibrations are removed by a performing conjugate gradient minimization to a local zero force configuration for which the icosahedral content is determined. Following the red curves, Figure 2 demonstrates that the liquid-like state at temperatures higher than Tg contains only a few icosahedral atoms, however as the temperature reduces and the glass transition regime is entered, the icosahedral content rapidly increases. Below Tg, it then saturates at the time-scale of the simulation to eventually become the as-quenched sample. The blue curves represent the direct quench after the 1000ns high temperature annealing protocol at a temperature just below Tg and show that such an annealing result in a significant rise in icosahedral content. Figure 1 shows that with this increased icosahedral content there is a reduction in cohesive energy and a decrease in the average volume per atom.
Figure 3 plots the cohesive energy and volume per atom as a function of icosahedral content using the data contained in Figure 1 & 2. Inspection of this figure reveals a linear relationship between energy/volume and icosahedral content for the three atomic concentrations considered. These results are consistent with previous MD simulations using a LJ model binary glass [32,33] which showed that the average energy and volume per atom reduction was directly related to the decrease in local bond frustration and local volume upon creation of icosahedral motives. The linear relation between energy and icosahedral content was also seen using another EAM potential [34]. The fact that such linear relations are seen for both an EAM potential and a model LJ binary glass system suggest a universal phenomenon-independent of the force model and driven by the balancing of internal stresses rather than energy minimization [32]. This picture is further supported by the gradients in Figure 3 being independent of the atomic concentration ratio, supporting the notion that a quite local mechanism is at play.
Inspection of the atom type underling the icoshadreal content reveals the icosahedral environments mainly involve the smaller Cu. When considering the icosahedral percentages only in terms of the Cu atoms, the 50:50 and 64:36 samples have similar fractions of icosadrally coordinated Cu atoms, whereas the 75:25 sample has a lower fraction. Indeed the 75:25 sample has an absolute icosahedral percentage like that of the 64:36 sample suggesting that there exists a maximum level of Cu icosahedral content irrespective of the fraction of Cu atoms. The origin of this is likely to lie in the constraints associated with icoshaedral connectivity and thus the MRO which has emerged at the timescale of the present MD simulations. This aspect we now consider by investigating the neighbouring connectivity between icosahedral environments.
Figure 2: Corresponding percentage of icosahedra as a function of temperature for Cu-Zr alloys. Red and blue lines represent as-quenched and 1000ns annealed samples, respectively.
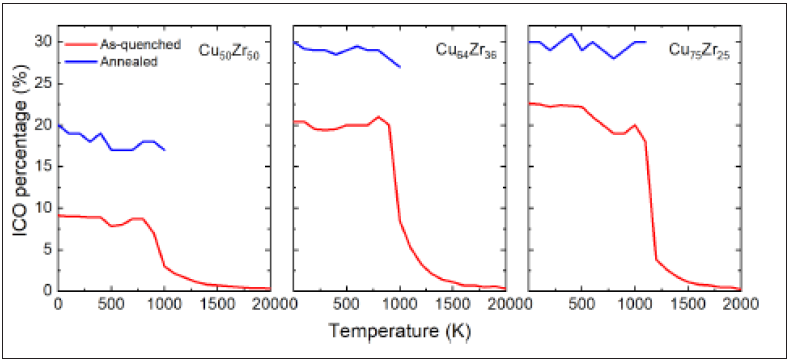
Figure 3: Cohessive energy and atomic volume as a function of icosahedral content. Each data point represents a configuration which has been quenched from configurations at Tg .
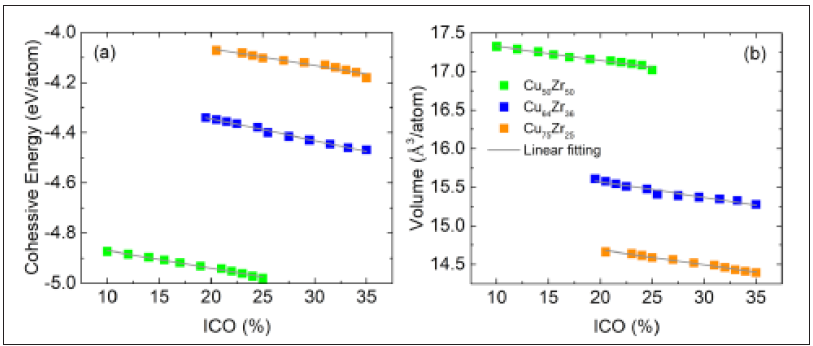
Figure 4 plots the ICA-connectivity of Lee et al. [44] as a function of time during the high-temperature protocol to produce the annealed sample. The data is shown in absolute percentages. Also shown is the ICA percentage. During the initial rapid increase in total icosahedral content a significant change in the populations of ICA-connectivity types is seen. Initially, the vertex- connections (involing one common neighbour) has the maximum percetange, but rapidly drops due primarily to an increase in the number of volume-connections (involving five common neighbours). After these large initial changes, both the number of volume-connections and face-connections (involving three common neighbours) steadily increasing, whilst the number of edge- connections (involving two common neighbours) remains largely unchanged. This trend is seen for all atomic-type concentration ratios. For the 50:50 concentration, a small population of isolated ICAs exist. Such isolated ICAs are absent in the 64:36 and 75:25 concentrations. Thus as the high-temperature structural relaxation proceeds, the increasing population of icosahedral environments appears more densely connected in terms of neareast neighbour ICAs. The data for 50:50 concentration demonstrates that newly created ICAs tend to be in regions of existing ICA content, since the number of isolated ICAs only negligibly decreases.
Figure 4: The percentage of the connectivity types between nearest neighbor icosahedral atoms in Cu-Zr alloys. By measuring the number of shared atoms between different icosahedra, five types of connectivity can be defined: no connection, vertex(sharing one atom)-, edge(sharing two atoms)-, face(sharing three atoms)-, and volume(sharing five atoms)- type connection.

Figure 5: Snapshots of the central atoms of icosahedra in (a) as-quenched and the (b) 1000ns annealed Cu64Zr36 samples at 50K. Only bonds whose length is shorter than 2.6Å that bond length of Cu are created. In figure(a), dotted circles indicate tetrahedron, hexagon, and nearly linear bonds. Visualization is via OVITO [43]. (c)schematic diagram of Laves phase polyhedron.
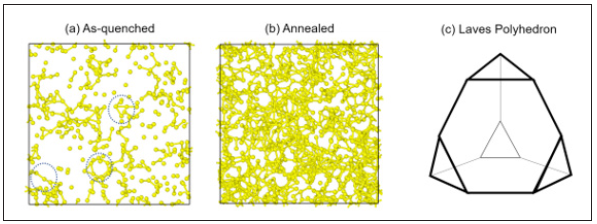
Some insight into the above trends can be gained by visually inspecting both the As-quenched and annealed samples. In Figure 5(a) & 5(b), snapshots of the as- quenched and the 1000 ns annealed Cu64Zr36 samples are displayed showing only the ICAs. Bonds connecting the nearest neighbour ICAs are also shown. A close analysis of this visual data reveals a network of small fragments of connected ICAs, in which the bonds form extended linear chains, triangles and tetraheda. The number of such structures increases upon relaxation. This conclusion is quantitatively confirmed through an analysis of the bond angle distribution. Figure 6 shows the bond-angle distribution for the as-quenched and the 1000 ns annealed samples. Consistent with snapshots of Figure 5(a) & 5(b), three types of bond angles of 60˚, 120˚, and 180˚ are preferred. High peaks at around 60˚ and 120˚ would result from accumulated ICAs with a large number of tetrahedron fragments, while a preference of the 180◦ type is representative of linear chains of nearest neighbour connected ICAs Figure 6 shows that long annealing times cause sharper peaks at the 60˚- and 120˚ -type bond angles.
Figure 6: Bond angle distribution of as-quenched (red) and annealed (blue) samples for (a)Cu50Zr50, (b)Cu64Zr36, and (c)Cu75Zr25. Inset figure represent weight of bond angle in crystallized Cu2Zr with laves phase.
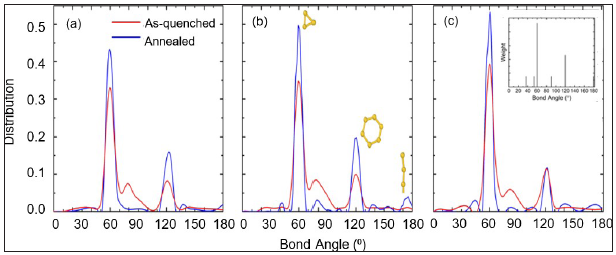
Such bonded structures suggest signatures of the Laves phase. Figure 5(c) plots the icoahedral back-bone of the Laves binary crystal structure and shows that triangular and pentagon structure exist within this ordered phase. Indeed, it is such fragments that are responsible for the peaks at 60˚- and 120˚-type seen in Figure 6. This conclusion is compatible with the work of Zemp et al. [46].
When comparing the final annealed sample to that of the asquenched sample, such fragments are isolated structures in the as-quenched sample whereas there exists a single system-spanning cluster of connected fragments in the more relaxed annealed sample. Because icosahedral environments indicates structures with minimal (bond energy) frustration, such percolating structures are expected to strongly the bulk mechanical properties. It is this aspect that we now considered.
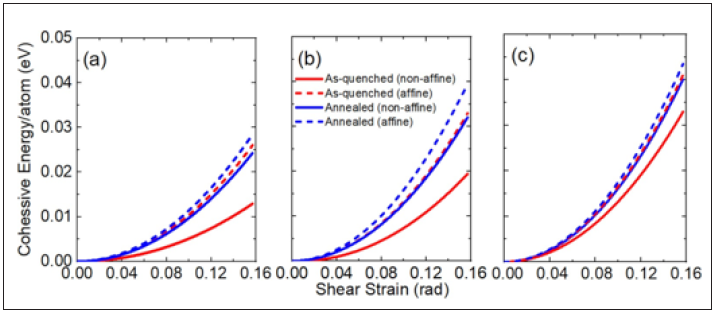
Athermal plasticityElastic constant via shear deformation: To calculate an elastic stiffness, both as-quenched and annealed samples are now shear strained by distorting the simulation cell. For distorting, pure shear is given along the x direction in the x-z plane with a fixed volume. To compare affine (non-relaxed) and non-affine (relaxed) deformations, we firstly take 0.04 degree (0.0006981317 rad) shear strain increment at 0 K and refer these samples as ”non-relaxed”. Then conjugate gradient minimization is repeated every 0.04 degree to a new local potential energy minimum and these samples are refered as ”relaxed”. Figure 7 presents cohessive energy with respect to the shear strain. As we expected, the higher Cu concentration makes the stronger stiffness. Also, stiffness of annealed samples is greater than that of as-quenched samples, and it is also enhanced through affine deformation. Interesting point is the difference cohessive energy between non-relaxed and relaxed samples, i.e., the gap between non-relaxed and relaxed cohessive energy is getting narrow with increasing Cu concentration. Consequentially, the difference of anneal
Figure 7: Cohessive energy of (a)50Zr50, (b)Cu64Zr36, and (c)Cu75Zr25 with respect to the shear strain. Solid and dotted lines represent non-affine (relaxed) and affine (non-relaxed) deformations, respectively. As-quanched and annealed samples are distinguished by red and blue colors.
Cu75Zr25 is almost negligible. These behaviors can be clearly quantified through calculation of shear modulus. An energy of the conuration with atomic volume Ω0 is described as
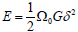
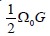 can be indicated as ν when
Figure 7 is fitted by quadratic function,
can be indicated as ν when
Figure 7 is fitted by quadratic function,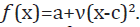 As a result,
the shear modulus G is simply calculated as
As a result,
the shear modulus G is simply calculated as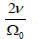 Caculated G is
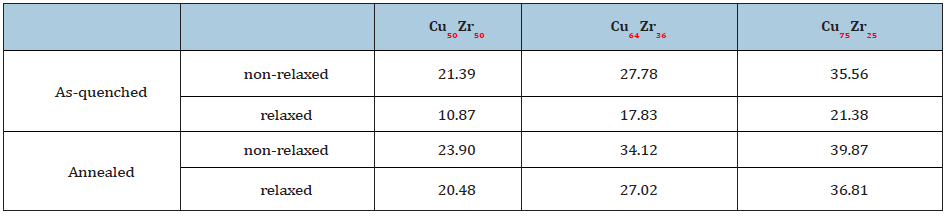
displayed in Table 1. In agreement with Figure 7, annealed samples
show the greater shear modulus than as-quenched samples, for
both ”non-relaxed” and ”relaxed”. Moreover, relaxed shear modulus
is drastically improved by annealing. For example, relaxed shear
modulus increases by over 15 MPa in annealed Cu75Zr25 compared
to as-quenched sample, while there is only 4 MPa increment in nonrelaxed
case.’
Caculated G is
displayed in Table 1. In agreement with Figure 7, annealed samples
show the greater shear modulus than as-quenched samples, for
both ”non-relaxed” and ”relaxed”. Moreover, relaxed shear modulus
is drastically improved by annealing. For example, relaxed shear
modulus increases by over 15 MPa in annealed Cu75Zr25 compared
to as-quenched sample, while there is only 4 MPa increment in nonrelaxed
case.’
Table 1:Shear modulus (MPa) of as-quenched and annealed CuxZr100−x (x=50,64,75) with affine (non-relaxed) and non- affine (relaxed) deformations.
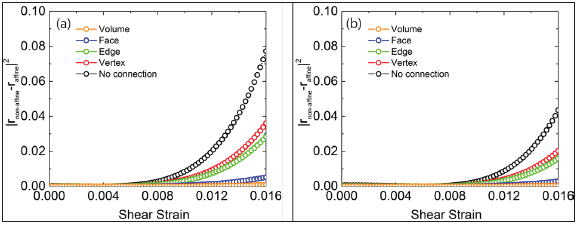
To examine further details in the structural stability of the icosahedra, we calculate the non-affine atomic displacement of icosahedral and non-icosahedral atoms, and present |rn.a.- ra.|2 in Figure 8, where n.a. and a. denote non-affine and affine, respectively. Interestingly, it seems that icosahedrally coordinated atoms are strongly bound in certain place while non-icosahedral atoms significantly move to find a new local potential energy minimum. Previous research [47] also determined that 13% of the icosahedra was in the group with the smallest displacement, while only 5% was in the group of the largest displacement. This evidence indirectly confirmed the results that shear transformation is favored at regions with less order [19,47,48] and relatively loose atomic packing [49-51]. The present analyses [47] and our results support an assumption that an icosahedra is structurally more stable and thus exhibit higher resistance to shear deformation.
Figure 8: Difference atomic displacement between affine (non- relaxed) and non-affine (relaxed) deformations (|rn.a.-ra.|2) of (a)Cu50Zr50, (b)Cu64Zr36, and (c)Cu75Zr25 with respect to the shear strain. Empty and solid circles represent non- icosahedral and icosahedral atoms, respectively. As-quanched and annealed samples are distinguished by red and blue colors.
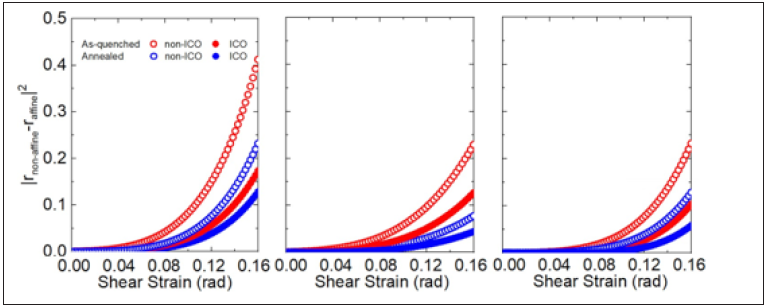
Figure 9(a) & 9(b) show a slice (1nm in thickness) of the asquenched sample. Red arrows represent displacement between affine and non-affine deformations. When we present atoms with larger displacement than 0.5Å in Figure 9(c), only non-icosaheral atoms are remained with random moving. On the contrary, all atoms with displacement with magnitude of smaller than 0.1Å is icosahedrally coordinated. These illustrated figures are well corresponded to Figure 8.
Figure 9: Sliced (a) top-view and (b) side-view of 1nm thick- ness of the as-quenched sample. ICO and non- ICO atoms are colored as yellow and white spheres, respectively. Red arrows represent displacement between affine and non-affine deformations. (c) displacement with magnitude of larger than 0.5Å. (d)displacement with magnitude of smaller than 0.1Å.
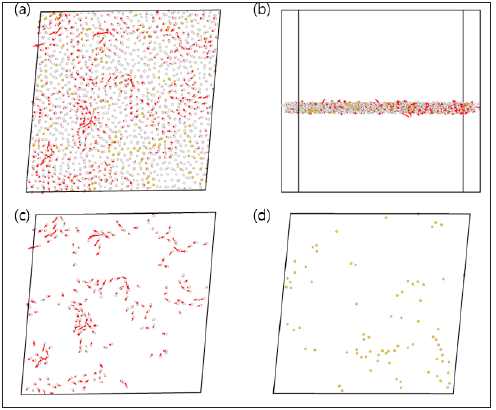
In case of icosahedral atoms, we further classify |rn.a.-ra.|2 by their connectivity types to examine the origin of the differences in the atomic mobility. Figure 10 clearly shows that isolated atoms (no connection) dominantly move, on the other hand, volume- and facetype connections which share a lot of atoms rarely respond to the shear strain. Furthermore, even isolated atoms are no- tably less active in annealed sample.
Figure 10: Difference atomic displacement between affine (non- relaxed) and non-affine (relaxed) deformations of connectivity types which are formed with icosahedral atoms in (a) as- quenched and (b) annealed Cu64Zr36 sample, as a function of the shear strain at 0K.
Tensile deformation: Because of the short time-scale restriction of the MD method, finite temperature atomistic simulations of deformation can mainly probe the high-strain rate athermal limit of plasticity [52, 53]. We investigate the effect of the degree of relaxation as well as Cu–Zr ratio on athermal plasticity, and study how such plasticity affects the underlying icosahedral structure.
Figure 11 shows the stress-strain curves for the as-cast and 1000ns annealed samples. The samples were subjected to uniaxial compressive loading at a constant strain rate equal to 107s−1 at a temperature of 50K (0.05Tg). As shown in the figure, the annealed samples show a greater stiffness and a higher peak stress than the as-cast samples. At large enough strains the subsequent flow stress is found to be independent of the degree of relaxation of the configuration prior to loading.
Figure 11: Annealing time dependent deformation of (a)Cu50Zr50, (b)Cu64Zr36, and (c)Cu75Zr25 with constant strain rate of 107s−1 at 50K. Red and blue lines represent as-quenched and 1000ns annealed samples, respectively.
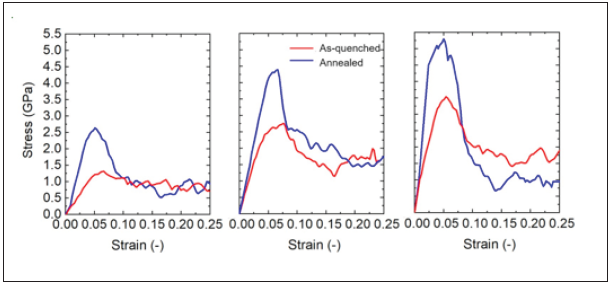
Figure 12 presents the variation of the icosahedral content for the as-quenched and 1000ns annealed samples with respect to the strain. Even though the annealed samples exhibit much larger number of icosahedral content than as-quenched sample in the elastic regime, both of icosahedral content sharply drop at around a breaking point of the deformation curve and show liquid-like behaviour. According to ref. [54], the icosahedral content drops in samples indicating structural excitation, as the plastic strain evolves beyond the peak stress response. Using the nearest neighbour connectivity classification scheme of Ref. [55], this “break up” of the icosahedral structure can now be better understood. Now, the changes in the fraction of different connectivity types were monitored with respect to the tensile strain to further understand the structural origin of the instability that occurs beyond the global yield. Figure 13 plots the percentage breakdown of the icosahedral connectivities as a function of strain for 1000ns annealed samples. The percentage of isolated icosahedral environments increases, as does the vertex- and edge-type connectivity. On the other hand, the face- and volume-type connectivity decrease. Interestingly, the volume-type connectivity (which is the only type to show an increase with annealing) reveals the most rapid de- cline. Such process occurs mainly in the transition regime from elasticity to plasticity, when the system’s stress is at its maximum. This is because, to sustain the global flow at the imposed strain rate, the icosahedral network structure has to give up to allow strain compatibility and sufficiently low viscosity [44, 56]. However, this structural state was almost saturated at strains beyond >0.1, achieving a steady-state flow. Together this suggests that as athermal plasticity proceeds and the structural state is excited the initial percolated icosahedral cluster under- goes fragmentation.
Figure 12: The percentage of icosahedral content with respect to the strain for (a)Cu50Zr50, (b)Cu64Zr36, and (c)Cu75Zr25 Tensile strain with a constant rate of 107s−1 at 50K. Red and blue lines represent as-quenched and 1000ns annealed samples, respectively.
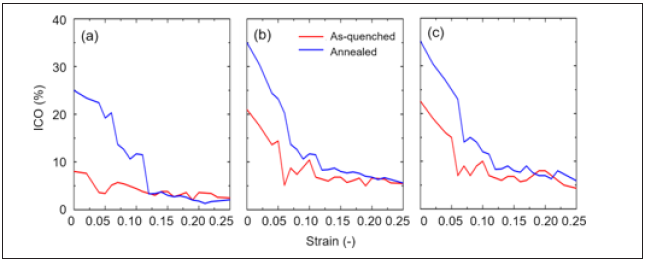
Figure 13: The percentage of the connectivity types between nearest neighbor icosahedra in 1000ns annealed Cu-Zr samples as a function of the tensile strain.

Figure 14 shows the bond-angle distribution of 1000ns annealed samples of before and after loading. The sharp peaks at specific bond angles are to be broaden after loading, which indicates decreasing number of icosahedral content and their shape distortion.
Figure 14: Bond angle distribution of before (solid line) and after (dotted line) loading of 1000ns annealed samples.

As mentioned in previous papers [19,48,50,57-60], it is known that the homogeneous plastic deformation preferentially occurs at the local regions with weak atomic connectivity. This deformation causes structural disordering, i.e., the destruction of highly connected clusters but creation of new isolated atoms [57,61], also found in Figure 13.
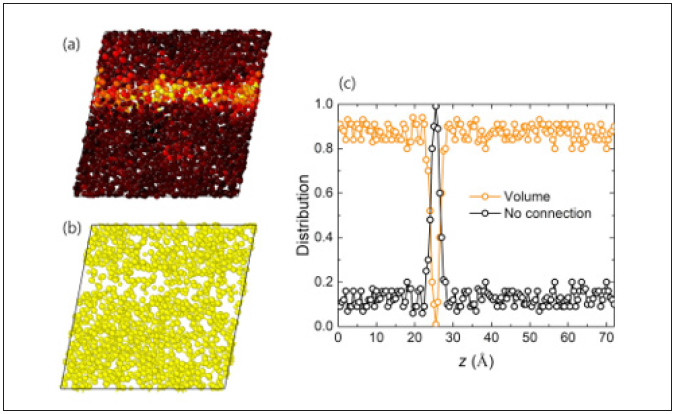
For last, by shear strain, we are able to find a single shear band in the Cu64Zr36 sample (Figure 15(a)), and surprisingly the shear band exists in a region with a relatively small number of icosahedral atoms (Figure 15(b)). Further, we investigate distribution of icosahedral connectivity types of volume and no connection along the z-direction of the corresponding state of Figure 15(a) & 15(b). It is found that the occurring shear band is due to a lack of icosahedral contents and resulting weak connections between of them.
Figure 15: (a) Failure through a single shear banding at 50K. The colour denotes the atomic shear strain. (b) Snapshots of the central atoms of icosahedra at a same state with figure (a). Visualization is via OVITO [43]. (c) distribution of volume-type connected icosahedral atoms and isolated icosahedral atom with respect to the z-direction of figure (a) and (b).
Conclusion
The structural and mechanical properties of Cu-Zr alloys in the glassy state were investigated by MD simulations. In well above the Tg, a large increase in the number of icosahedral contents was observed by decreasing temperature, especially at around Tg. Additionally, a long-time annealing process close to the Tg generated another significant increase in number of icosahedra.
In perspective of MROs, such large amount of icosahedrally coordinated Cu atoms (smaller atoms) connect with the nearest neighbor atoms and form a huge cluster which can be considered to be the most rigid backbone as a result. It was found that volumetype connectivity (shares five atoms) eventually dominates as structural re- laxation proceeds, while vertex-type connectivity (shares one atom) is mainly involved in the as-quenched sample.
We also provided the effect of the degree of relaxation on athermal plasticity, and how such plasticity affects the underlying icosahedral structure. The annealed samples show a greater stiffness and a greater yield strength than the as-cast samples. With a uniaxial loading, the percentage of isolated icosahedra (no connection), the vertex- and edge-type connectivity increase, while the face- and volume-type connectivity decrease. In addition, the sharp peaks at specific bond angles in the bond-angle distribution are to be broaden after loading, which indicates decreasing number of icosahedral content and their shape distortion.
For last, the elastic stiffness was calculated via shear transformation. Annealed samples show a greater shear modulus than as-quenched samples, which consists with stress–strain curves obtained by uniaxial loading. When shear modulus of affine deformations is always larger than that of non-affine deformation, this is mostly due to migration of nonicosahedrally coordinated atoms and some contribution comes from isolated icosahedral atoms.
From these results, we suggest that icosahedral con- tent in an amorphous structure plays a key role to deter- mine the structural stability and the mechanical proper- ties such as rigidity and maximum stress carrying capacity.
Future Works
Both MD simulations [31,62] and the ARTn method [13,14,62] reveal localized structural excitations (LSEs) taking the form of extended string-like and ring-like atomic displacements. The structural environment around such LSEs has yet to be investigated in terms of icosahedral content and connectivity. In particular, does the extended string-like geometry of the LSE correlate with the surrounding icosahedral structure? Is there also a statistical difference in the energy landscape for LSEs associated with the creation of icosahedral content? Answers for these questions would give a better understanding of the analogy of alpha and beta processes in BMGs.
References
- Johnson WL (1999) Bulk glass-forming metallic alloys: Science and MRS Bulletin 24(10): 42-56.
- Ashby MF, Greer AL (2006) Metallic glasses as structural Scripta Materialia 54(3): 321-326.
- Schuh CA, Hufnagel TC, Ramamurty U (2007) Mechanical behavior of amorphous alloys. Acta Materialia 55(12): 4067-4109.
- Wang WH, Dong C, Shek CH (2004) Bulk metallic Materials Science and Engineering: Reports 44(2-3): 45-89.
- Inoue A (2000) Stabilization of metallic supercooled liquid and bulk amorphous Acta Materialia 48(1): 279-306.
- Jiang Y, Qiu K (2015) Computational micromechanics analysis of toughening mechanisms of particle-reinforced bulk metallic glass composites. Materials & Design (1980-2015) 65: 410-416.
- Bruck HA, Christman T, Rosakis AJ, Johnson WL (1994) Quasi-static constitutive behavior of zr 25ti13. 75ni10cu12. 5be22. 5 bulk amorphous alloys. Scripta Metallurgicaet Materialia 30(4): 429-434.
- Gu XJ, Dermott AG, Poon JS, Shiflet GJ (2006) Critical poisson’s ratio for plasticity in Fe-Mo-C-B-Ln bulk amorphous Applied Physics Letters 88(21): 211905.
- Akihisa I, Shen B, Koshiba H, Kato H, Yavari AR (2003) Cobalt-based bulk glassy alloy with ultrahigh strength and soft magnetic properties. Nature Materials 2(10): 661-663.
- Louzguine DV, Yavari AR, Inoue A (2003) Devitrification behaviour of Cu-Zr-Ti-Pd bulk glassy Philosophical Magazine 83(26): 2989-3003.
- Spaepen F (1977) A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metallurgica 25(4): 407-415.
- Chen M (2008) Mechanical behavior of metallic glasses: microscopic understanding of strength and Annu Rev Mater Res 38: 445-469.
- Swayamjyoti S, L¨offler JF, Derlet PM (2014) Local structural excitations in model glasses 89(22): 224201.
- Swayamjyoti S, L¨offler JF, Derlet PM (2016) Local structural excitations in model glass systems under applied load. Physical Review B 93(14): 144202.
- Falk ML, Langer JS (1998) Dynamics of viscoplastic deformation in amorphous Physical Review E 57(6): 7192-7205.
- Maloney C, Lemaitre A (2004) Subextensive scaling in the athermal, quasistatic limit of amorphous matter in plastic shear Physical Review Letters 93(1): 016001.
- Maloney C, Lemaitre A (2004) Universal breakdown of elasticity at the onset of material failure. Physical Review Letters 93(19): 195501.
- Demkowicz MJ, Argon AS (2005) Liquidlike atomic environments act as plasticity carriers in amorphous silicon. Physical Review B 72(24): 245205.
- Shi Y, Falk ML (2006) Atomic-scale simulations of strain localization in three-dimensional model amorphous solids. Physical Review B 73(21): 214201.
- Guan P, Chen M, Egami T (2010) Stress-temperature scaling for steady-state flow in metallic Physical Review Letters 104(20): 205701.
- Zadeh MJ, Tavakoli R, Srolovitz DJ, Zhang YW (2016) Thermally induced failure mechanism transition and its correlation with short- range order evolution in metallic glasses. Extreme Mechanics Letters 9: 215-225.
- Sopu D, Able K (2015) Influence of grain size and composition, topology and excess free volume on the deformation behavior of Cu-Zr Beilstein Journal of Nanotechnology 6(1): 537-545.
- Manning ML, Langer JS, Carlson JM (2007) Strain localization in a shear transformation zone model for amorphous Phys Rev E Stat Nonlin Soft Matter Phys 76(5): 056106.
- Langer JS (2008) Shear-transformation-zone theory of plastic deformation near the glass Physical Review E 77(2): 021502.
- Falk ML, Langer JS, Pechenik L (2004) Thermal effects in the shear-transformation-zone theory of amorphous plasticity: comparisons to metallic glass data. Phys Rev E Stat Nonlin Soft Matter Phys 70(1): 011507.
- Nelson DR (1983) Liquids and gasses in spaces of incommensurate curvature. Physical Review Letters 50(13): 982.
- Nelson DR (1983) Order, frustration, and defects in liquids and glasses. Physical Review B 28(10): 5515.
- Steinhardt PJ, Nelson DR, Ronchetti M (1983) Bond-orientational order in liquids and Physical Review B 28(2): 784.
- Cheng YQ, Ma E (2011) Atomic-level structure and structure-property relationship in metallic glasses. Progress in materials science 56(4): 379-473.
- Sha ZD, Feng YP, Li Y (2010) Statistical composition- structure-property correlation and glass-forming ability based on the full icosahedra in Cu-Zr metallic glasses. Applied Physics Letters 96(6): 061903.
- Derlet PM, Maaß R (2017) Thermal processing and enthalpy storage of a binary amorphous solid: A molecular dynamics Journal of Materials Research 32(14): 2668-2679.
- Derlet PM, Maaß R (2018) Local volume as a robust structural measure and its connection to icosahedral content in a model binary amorphous Materialia 3: 97-106.
- Derlet PM, Maaß R (2018) Thermally activated stress relaxation in a model amorphous solid and the formation of a system-spanning shear Acta Materialia 143: 205-213.
- Ding J, Cheng YQ, Ma E (2014) Full icosahedra dominate local order in cu64zr34 metallic glass and supercooled Acta Materialia 69: 343-354.
- Foiles SM, Baskes MI, Daw MS (1986) Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Physical Review B 33(12): 7983.
- Finnis MW, Sinclair JE (1984) A simple empirical n-body potential for transition metals. Philosophical Magazine A 50(1): 45-55.
- Xu D, Lohwongwatana B, Duan G, Johnson WL, Garland (2004) Bulk metallic glass formation in binary cu- rich alloy series-cu100- xzrx (x= 34, 36, 38.2, 40 at.%) and mechanical properties of bulk cu64zr36 glass. Acta Materialia 52(9): 2621-2624.
- Plimpton S, Crozier P, Thompson A (2007) Lammps- large-scale atomic/molecular massively parallel simulator. Sandia National Laboratories.
- Mendelev MI, Kramer MJ, Ott RT, Sordelet DJ, Yagodin, et al. (2009) Development of suitable inter- atomic potentials for simulation of liquid and amorphous Cu-Zr alloys. Philosophical Magazine 89(11): 967-987.
- Evans DJ, Holian BL (1985) The nose-hoover thermostat. The Journal of chemical physics 83(8): 4069-4074.
- Sha ZD, Feng YP, Li Y (2011) The fundamental structural factor in determining the glass-forming ability and mechanical behavior in the Cu-Zr metallic glasses. Materials Chemistry and Physics 127(1-2): 292-295.
- Antonowicz J, Pietnoczka A, Drobiazg T, Almyras GA, Papageorgiou DG, et al. (2012) Icosahedral order in Cu-Zr amorphous alloys studied by means of X-ray absorption fine structure and molecular dynamics simulations. Philosophical Magazine 92(15): 1865-1875.
- Stukowski A (2009) Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Modelling and Simulation in Materials Science and Engineering 18(1): 015012.
- Lee M, Lee CM, Lee KR, Ma E, Lee JC (2011) Networked interpenetrating connections of icosahedra: Effects on shear transformations in metallic glass. Acta Materialia 59(1): 159-170.
- Jerome Z, Massimo C, Schonfeld B, Jorg FL (2014) Icosahedral superclusters in cu 64 zr 36 metallic glass. Physical Review B 90(14): 144108.
- Zemp J, Celino M, Schonfeld B, Loffler JF (2015) Crystal-like rearrangements of icosahedra in simulated copper-zirconium metallic glasses and their effect on mechanical properties. Physical review letters 115(16): 165501.
- Cheng YQ, Cao AJ, Sheng HW, Ma E (2008) Local order influences initiation of plastic flow in metallic glass: Effects of alloy composition and sample cooling history. Acta Mater 56(18): 5263-5275.
- Yunfeng S, Michael LF (2005) Strain localization and percolation of stable structure in amorphous solids. Physical Review Letters 95(9): 095502.
- Masato W, Yoji S, Shigenobu O, Junyoung P (2007) Relationship between local geometrical factors and mechanical properties for cu-zr amorphous alloys. Intermetallics 15(2): 139-144, 2007.
- Jae-Chul L, Kyoung-Won P, Kyou-Hyun K, Eric F, Byeong-Joo L, et al. (2007) Origin of the plasticity in bulk amorphous alloys. Journal of Materials Research 22(11): 3087-3097.
- Kyoung-Won P, Chang-Myeon L, Masato W, Yoji S, Michael LF, et al. (2008) Elastostatically induced structural disordering in amorphous alloys. Acta Materialia 56(19): 5440-5450.
- Todd CH, Christopher AS, Michael LF (2016) Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Materialia 109: 375-393.
- Christian B, Peter MD, Helena VS (2009) Strain rates in molecular dynamics simulations of nanocrystalline metals. Philosophical Magazine 89(34-36): 3465-3475.
- Sun Y, Concustell A, Greer AL (2016) Thermomechanical processing of metallic glasses: extending the range of the glassy state. Nature Reviews Materials 1: 16039.
- Soklaski R, Nussinov Z, Markow Z, Kelton KF, Yang L (2013) Connectivity of icosahedral network and a dramatically growing static length scale in Cu-Zr binary metallic glasses. Physical Review B 87(18): 184203.
- Fabio A, Michael LF (2005) Shear softening and structure in a simulated three-dimensional binary glass. The Journal of chemical physics 122(15): 154508.
- Cheng YQ, Cao AJ, Sheng HW, Ma E (2008) Local order influences initiation of plastic flow in metallic glass: Effects of alloy composition and sample cooling history. Acta Materialia 56(18): 5263-5275.
- Park KW. Wakeda M, Shibutani Y, Fleury E,Jae-Chul L (2008) Effect of the atomic packing density on the structural change rate of amorphous alloys under elastostatic stress. Met Mater Int 14: 159-163.
- Cao AJ. Cheng YQ, Ma E (2009) Structural processes that initiate shear localization in metallic glass. Acta Mater 57(17): 5146-5155.
- Sang-Chul L, Chang-Myeon L, Jae-Chul L, Hwi- Jun K, Shibutani Y, et al. (2008) Structural disordering process of an amorphous alloy driven by the elastostatic compression at room temperature. Applied Physics Letters 92(15): 151906.
- Kyoung-Won P, Jaeil J, Masato W, Yoji S, ae-Chul L (2007) Atomic packing density and its influence on the properties of cu-zr amorphous alloys. Scripta Materialia 57(9): 805-808.
- Soyoung J, Derlet PM, Loffler FL (2018) Geometrical characterization of atomic structure of cu-zr bulk metallic glasses.
© 2019 Soyoung Jekal. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






