Metabolic Rate and Clothing Estimation for Thermal Comfort Inference

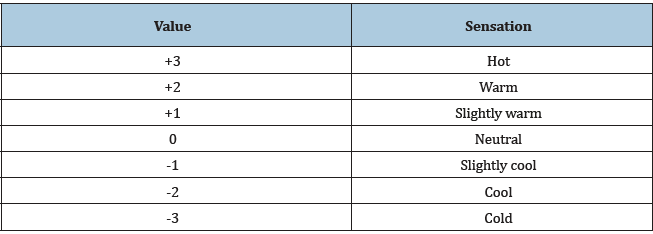
Indoor thermal comfort modelling introduces a field of research closely related to the occupants’ well-being, attendance and cognitive performance [1]. The regulation of the thermal conditions is conducted trying to eliminate any negative effects on the occupants’ feeling or execution of activities [2]. Thermal comfort is defined as «the condition of mind in which satisfaction is expressed with the thermal environment» [3]. Two key parameters that have a strong impact on thermal comfort are metabolic rate (M) and clothing insulation (Icl). Those parameters are usually estimated according to certain tables provided by Ashrae [3]. In this work, M and Icl are predicted utilizing feedback provided by the building occupants regarding their thermal sensation, measured on the ASHRAE 7-point range (Table 1).

Table 1:ASHRAE 7-point thermal sensation range.

Thermal comfort is being calculated using Fanger’s equation which uses the Predicted Mean Vote index to quantify the degree of thermal discomfort on the above scale [4]:

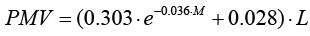
where L is defined as:

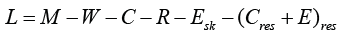
Where M(W/m²) is the internal energy production, W(W/m²) is the external work, C(W/ m²) is the heat loss by convection, R(W/m²) is the heat loss by thermal radiation Esk(W/m²) is the heat loss by evaporation of the skin, Cres(W/m²) and Eres(W/m²) are the sensible and the evaporation heat loss due to respiration respectively.

PMV calculation from Fanger’s equation requires the definition of 2 additional variables, besides M and Icl: Temperature (T) and Humidity (H). In the current study, T and H are available by sensor measurements while M and Icl are initialized utilizing the ASHRAE tables [3]. The goal is to personalize each occupant’s perception of the indoor thermal environment by utilizing the PMV feedback provided in order to revise the M and Icl values that are initially assumed. For this purpose, a model that utilizes T, H and PMV_feedback as inputs to predict M and Icl values according to Fanger’s equation, is built. The formulated problem is a multitarget regression problem so an appropriate regressor is selected.

Figure 1:Thermal comfort inference flow chart.

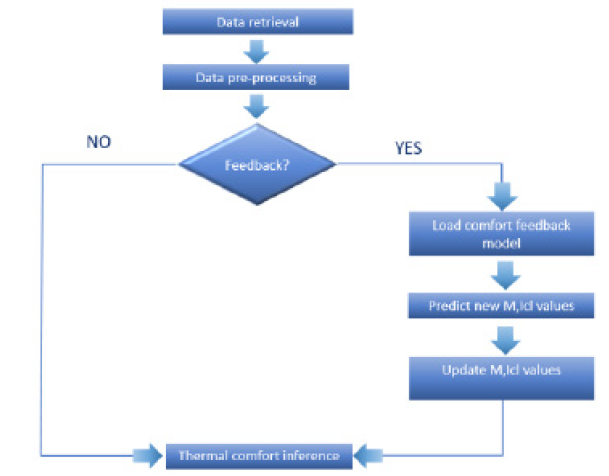
Extremely Randomized Trees (Extra trees) is an algorithm for ensemble tree construction based on extreme randomization [5]. The algorithm’s advantage at predicting multiple output values is highlighted by the fact that all the target variables are predicted simultaneously using one model in contrast to the local methods that predict each target variable separately. The algorithm uses the whole learning sample and not a bootstrap replica for the tree growing, while the procedure of selecting cut-points for splitting the nodes is performed randomly. As presented in Figure 1, the algorithm is executed as described in the following steps:

1. All the necessary data are retrieved (T, H, M, Icl).

2. Data are preprocessed to handle abnormalities (nulls etc.)

3. It is checked whether feedback is provided by the user.

If there is feedback then the comfort feedback predictive model is loaded and new M, Icl values are calculated.

4. Thermal comfort is calculated using Fanger’s equation.

The algorithm’s efficiency was tested on a broad range of feedback values (from -3 to +3), comparing the final results with the baseline Fanger model. It is observed that high accuracy is achieved, the errors are minimized (Figure 2) (Table 2).

Table 2:Error analysis of the tested observations.

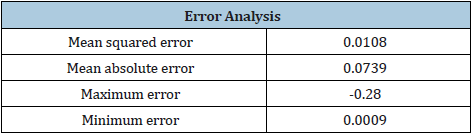
Figure 2:Feedback and PMV using the predicted M, Icl values.

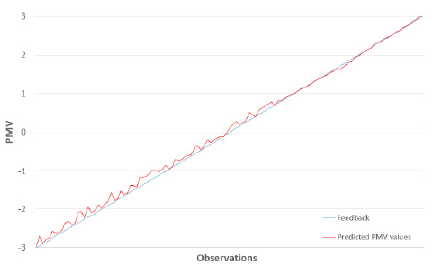
The predictions for M and Icl values are accurate for the whole range of the 7-point thermal range. This means that different perceptions of the thermal environment can be interpreted successfully, creating adaptive models for each occupant based on their dressing preferences and activity routines. The values of Mean Squared Error (MSE) and Mean Absolute Error (MAE) are 0.0108 and 0.0739 respectively, which is an error that is in fact imperceptible.

The proposed method, utilizes user feedback aiming at confining the subjective factor enclosed in Fanger’s static model, which is the most commonly used thermal comfort inference model. As a result, the accuracy of the inferred comfort values is improved while new, more flexible models that can be applied to groups of people with specific characteristics may be designed. Achieving the optimal thermal comfort may as well contribute towards household energy consumption reduction by optimizing the function of the HVAC system, customized to the occupants’ needs.

This work is partially supported by the “enCOMPASSCollaborative Recommendations and Adaptive Control for Personalized Energy Saving” project funded by the EU H2020 Programme, grant agreement no.723059.

1. Mendell MJ, Heath GA (2005) Do indoor pollutants and thermal conditions in schools influence student performance? A critical review of the literature. In Indoor Air 15(1): 27-52.
2. Djongyang N, Tchinda R, Njomo D (2010) Thermal comfort: A review paper. Renewable and sustainable energy reviews 14(9): 2626-2640.
3. (2004) Standard 55-Thermal environment conditions for human occupancy. ANSI/ASHRAE.
4. Fanger PO (1970) Thermal comfort, analysis and application in environmental engineering. Danish Technical Press, Copenhagen, Denmark.
5. Geurts P, Ernst D, Wehenkel L (2006) Extremely randomized trees. Machine Learning 63(1): 3-42.