- Submissions

Full Text
Research & Development in Material Science
Reliability Studies Based on the Tensile Properties of the Polymer Nanocomposites
Subhash Mandal1*, Debmalya Roy1 and Namburi Eswara Prasad2
1Directorate of Nanomaterials and Technologies (DNMAT), India
2DMSRDE, DRDO, India
*Corresponding author:Subhash Mandal, Directorate of Nanomaterials and Technologies (DNMAT), Defence Materials and Stores Research & Development Establishment (DMSRDE), India
Submission: August 12, 2019;Published: August 21, 2019

ISSN: 2576-8840 Volume11 Issue3
Abstract
In the present study, two different blends were used as matrix. One of the blends is consisting of the two semi-crystalline polymeric components. The other blend is the combination of one semi-crystalline polymer and one amorphous polymer. The semi-crystalline poly (ether ketone) (PEEK) is the common component in both the blends. The other polymers are poly (ether ketone) (PEK) which is semi-crystalline and poly (ether sulphone) (PES) which is amorphous in nature. The blends were optimized based on their thermal and mechanical properties. Twin screw extrusion technique was used for the incorporation of nanoparticles of barium titanate (BT). The nano filler of BT was varied from 2 to 6wt% (0.41 to 1.28 vol%). The fabricated nanocomposites were tested for tensile properties such as tensile strength, tensile modulus and elongation at break. ‘Pukanszky model’ related to tensile strength was used to evaluate the reliability of the tensile data of the fabricated polymer nanocomposites obtained from the experimental results. From ‘Pukanszky model’, it was observed that tensile strength seemed to govern by the adhesion parameter, Bσ, which correlates the interphase and the interfacial interaction.
Keywords:Nanocomposite; Extrusion; Tensile strength; Tensile modulus; Reliability
Introduction
Polymer composites based on the high-performance thermoplastic polymers have many advantages and used for the various applications viz. bearings, brakes, clutches, gears, automation machinery in office, rollers and seals, pads of tank track, transmission belts along with many others [1-5]. The combination of superior thermo-mechanical properties causes poly (ether ketone) (PEEK) as a promising candidate for applications under chemical environment at high temperatures [6-10]. Poly (ether ketone) (PEK) is also semi crystalline polymer with glass transition temperature of 155 ℃ and melting point of 365 ℃ [11]. Poly (ether sulphone) (PES) is an amorphous polymer with a high Tg and can be classified as a thermally stable polymer. Among other interesting properties of PES, are good hydrolytic and thermo-oxidative stability, high rigidity and creep resistance. The high Tg of PES suggests the polymer as a suitable candidate for developing PEEK based blends [12,13]. Various studies have been carried out by different researchers on PEEK based composites [14-16]. However enormous scopes are still left to study in depth and details.
The structural performance, durability and reliability of the polymer composites can be correlated with three types of internal defects. The first type of defects is chemical structure defects. The size of the defects is in the range of 10-l00Å which control the critical design parameters viz. dimensional changes, glass transition temperature (Tg) and moisture absorption. This can be easily controllable by the chemical analysis of the raw materials prior to the manufacturing. The second type of defects is manufacturing defects. The size of the defects is greater than l0μm. The defects include debonds, inclusions and voids which are directly correlated with manufacturing process control and evaluated by optical scanning, ultrasonics and other characterization techniques sensitive to the interfacial imperfections. The combination of these two types of intrinsic defects with the mechanical and environmental stresses results a third type of macroscopic fatigue defects viz. interconnected microcracks followed by macroscopic crack growth. This type of cracks can be identified by the ultrasonic emission and visual inspection. The recognition of intrinsic structural defects and their contributions to polymer composite reliability is an important extension in the analytic modeling and reliability predictions for the structural polymers and high strength fiber reinforced composites. This discussion introduces the mathematical predictive models for the polymer composite reliability [17]. The main objective of the article is the reliability studies of the polymer nanocomposite using various theoretical models related to tensile properties and experimental results.
Materials and Methods
Materials used
The materials used in this study were PEEK (Victrex 450G) and PEK (P-22) from ICI Co., PES (Trade name: RADEL, Grade: A-300) from Amoco Performance Products (Alpharetta, GA, USA) and Barium titanate (BaTiO3) nanoparticles (synthesized at the laboratory). PEEK is a semi crystalline polymer with glass transition temperature of 143 ℃, a melting point of 345 ℃ [11]. PEK is also semi crystalline polymer with glass transition temperature of 155 ℃ and melting point of 365 ℃ [11]. PES is an amorphous polymer with high glass transition temperature of 216 ℃ and melting point of 335 ℃ [13]. The densities of PEEK, PEK and PES are 1.303g/ cm3, 1.317 g/cm3 and 1.370g/cm3 respectively. Barium titanate (BT) nanoparticles were synthesized by sol-gel technique [18]. The particle size of BaTiO3 were 25-80nm. The density and melting point of BaTiO3 was 6.01g/cm3 and 1650 ℃ respectively. The nanocomposites were prepared following the procedure described elsewhere [11,13]. The fabricated nanocomposites were tested for tensile properties as per the reported method [11,13].
Preparation of composites
PEEK/PES blend in the ratio of 75:25 (wt%) and PEEK/PEK blend in the ratio of 80:20 were taken as the optimized blends [11,13]. The optimized blends were predried at 120 ℃ for 5h to remove the volatile contents and moisture. Barium titanate (BT) nanoparticles were incorporated in various concentrations viz. 2, 4 and 6 wt% into the optimized blends. The compounding for the preparation of nanocomposites was done in Prism Eurolab-16 twin-screw extruder. The molten extrudate was quickly quenched in a water bath to room temperature. The compound thus obtained were collected as strands and cut into granules using automatic chopper. The chopped granules were again pre-dried at 120 ℃ for 10h and molded by injection molding for further characterization.
Characterization
The thermal behavior of the PEEK/PES/BT nanocomposites was evaluated using Universal TA instrument (differential scanning calorimeter V4.5A). The weight of all samples was 5-7mg, and these samples were heated to 400 ℃ at constant heating rate of 10 ℃/min under nitrogen atmosphere to study the melting behavior and held for 5min to remove the previous thermal history. Non-isothermal crystallization was investigated by cooling the samples from 400 ℃ to 50 ℃ at constant cooling rate of 10 ℃/min.
Tensile properties were determined by a universal testing machine (Zwick 1773) at room temperature. The injection molded samples of standard tensile (ASTM D638) bar. The cross-head separation was 6cm and cross-head speed was 5mm/min during the tensile test following the ASTM D638 test method [19]. A minimum of five samples were tested for each composition and their average value within ±3.5% is reported. The test was performed at ambient temperature 303±2K. Compounded materials were used in a scanning electron microscope (CARL ZEISS EVO-50) to study the morphology of the blends and nanocomposites samples. The acceleration voltage used was 10kV and the magnification was 1000X and 3.5kX for the blend and nanocomposite samples respectively. The samples were coated with a thin layer of gold by using a vacuum sputtered prior to SEM observations.
Theoretical predictive models
The effect of specific nano filler viz. barium titanate (BT) nanoparticles in the nanocomposite along with the reliability study can be carried out using the following theoretical models related to tensile strength and modulus. However, we have considered few of these models to represent and discuss our experimental data.
Models related to tensile modulus:
Model 1: Guth and Smallwood Model [20,21]
For spherical particles
For non-spherical particles
Where E = tensile modulus; Ф= volume fraction;
c, m, d indicates composite, matrix, dispersive phase, respectively;
KE = Einstein coefficient [22] = 2.5 for spherical particles
α = reinforcement aspect ratio [23]=1.0-1.3
Model 2: Takayanagi’s model [24]
A three phase-model, proposed by Ji et al. [25], taking into account the matrix, the filler particles and the interphase. For plate particles having thickness tc and both length and width ξc (with ξc » tc), tensile modulus can be expressed as of the following Eq. (9)
Where  ; Ec, Em and
Ef are tensile modulus of the composite, matrix and the filler,
respectively; τ is the thickness of the interface; Фd is the filler volume
fraction; and k=Ei(0)/Em is the ratio of the interphase modulus on
the surface of the particle, Ei(0), to that of the matrix, Em. This three
phase model assumes linear dependence of the modulus on space
variable, when passing from the matrix to the surface of the particle.
The controlling parameters for the mechanical properties of the
materials are the two characteristic dimensions of the dispersed
particles, tc and ξc, the thickness of the interphase, τ, the ratio Ef/Em
and the parameter k. If the influence of the interfacial region can be
neglected, corresponding to τ=0 (means α=β), then the three-phase
model reduces to the two-phase Takayanagi’s model [24] Eq. (4).
; Ec, Em and
Ef are tensile modulus of the composite, matrix and the filler,
respectively; τ is the thickness of the interface; Фd is the filler volume
fraction; and k=Ei(0)/Em is the ratio of the interphase modulus on
the surface of the particle, Ei(0), to that of the matrix, Em. This three
phase model assumes linear dependence of the modulus on space
variable, when passing from the matrix to the surface of the particle.
The controlling parameters for the mechanical properties of the
materials are the two characteristic dimensions of the dispersed
particles, tc and ξc, the thickness of the interphase, τ, the ratio Ef/Em
and the parameter k. If the influence of the interfacial region can be
neglected, corresponding to τ=0 (means α=β), then the three-phase
model reduces to the two-phase Takayanagi’s model [24] Eq. (4).
According to Ji et al. [25] the smaller particles provide an increasing modulus for the resulting composite as compared to the large particles because the interfacial region greatly affects Ec. However, when the size of the fillers is in the scale of micrometers, the influence of the interfacial region is neglected. In this case, as nanoparticles were used, thickness of the interfacial region can be assumed to tend to zero.
Model 3: Hashin-Shtrikman model [26],/
The two-phase model related to tensile modulus proposed by Hashin [26] who took into account the poisson contraction of the constituent phases. The overall response of the composite was assumed to be isotropic and linearly elastic. The equations for the lower and upper bounds are given in Eq. (5) and Eq. (6), respectively.
Where K and G are the bulk and shear moduli and m and d refers to matrix and dispersed phase, respectively.
Models related to the tensile strength:
Model 4: Pukanszky model: [27-29]
Where the fraction [(1-Фd)/(1+2.5Фd)] takes into consideration the decrease of the effective load bearing cross-section [30], and the exponential describes all other effects resulting in an increase of the tensile strength. σc and σm is the tensile strength of composites and matrix respectively.
From the physical point of view, the parameter Bσ is governed by the interface and interphase properties. Indeed, as shown by Rong et al. [31] for polypropylene nanocomposites, larger Bσ values correspond to higher interfacial adhesion. The following Bσ expression underlines these effects:
Where τ, the thickness of the interphase, is proportional to the interfacial adhesion, defined by the parameter γ12, with τ=λγ12, where λ is constant. The quantities ρf, Sf and σi represent the density of the filler material, the specific surface area of the filler and the yield stress of the interphase, respectively. Since it is virtually impossible to provide exact values for the absolute thickness τ and for the yield stress σi of the interphase, the parameter Bσ was determined from the experimental data using the following expression, derived from Eq. (7):

Results and Discussion
Tensile properties
The tensile properties were first determined from the primary stress-strain curves of the blends and nanocomposites (not shown).
Tensile modulus: The effect of nano-fillers in the nanocomposites, the experimental data were analyzed using the simple statistical model following “rule of mixture” [32,33], Eq. (10),
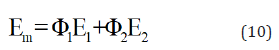
Where, Em is the modulus of the blend. E1 and E2 are the modulus of two different components of blends. Φ1 and Φ2 are volume fraction of two different components of blends. As there is no widely accepted addition rule available for the modulus (or strength) of nanocomposites, so it is evaluated by the “modified rule of mixture for discontinuous reinforcement” [2,34] Eq. (11).
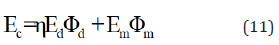
In this equation, E and Φ are the tensile modulus and volume fraction, respectively, the subscripts c, d, and m represent the composite, dispersed particle, and the matrix (PEEK/PEK and PEEK/PES blends), respectively. The strengthening efficiency coefficient, η, decreases with decreasing the reinforcement aspect ratio. Extending the aspect ratio of 10-100 for short fibers to the range of nanoparticles with an approx. aspect ratio of ~1, η is assumed to be approx. 0.1 [34]. The ‘rule of mixture’ showed lower value of relative modulus of nanocomposites than experimental results. The deviation was observed because the assumed values (viz. η) used in the “modified rule of mixture for discontinuous reinforcement” in equation (11). The dispersed nano-filler increases stiffness of the polymer blends (PEEK/PEK and PEEK/ PES) used as matrix. Also, the “modified rule of mixture for discontinuous reinforcement” does not contain any parameters or function related to the interfacial adhesion and crystallinity. As a result, the interfacial adhesion varies due to the heterogeneous nucleation in the nanocomposites exhibiting the deviation between ‘experimental results’ and ‘rule of mixture’. This result we have discussed in detail in our previous papers [11,13].
The significant deviation was observed from the experimental results for all aspect ratio (AR) i.e. AR=1.0, AR=1.2 and AR=1.3 in ‘Guth and Smallwood model’. The Takayanagi’s model showed closely fitted results up to 4wt% nano-filler loading. Thereafter, the decrease in the relative tensile modulus was found due to weaker interfacial interaction at 6wt% nanofiller loading. However, good correlation with the experimental results is observed in the lower boundary of the Hashin-Shtrikman model. This result we have already reported in details in our previous papers [11,13].
For prediction of moduli of a filled system, no attempt was made to discuss different approaches in detail, but different hypothetical theories are demonstrated. However, Hashin [35] & Hill [36] discussed the theoretical base for the reader. The solution model of lower and upper boundary assumes that individual phases are in uniform stress or strain condition.
However, practically, filler particles cannot be completely isolated from each other and also the reinforcement element might effectively be the aggregate of various smaller particles. So, the uneven stress distribution under load between the aggregates and particles is clearly an oversimplification because of the assumptions of uniform strain.
To increase the accountability of complex stress and the phase distribution, the different models are considered for different combinations of upper and lower boundary of rule of mixtures. For furnishing the phenomenological description of experimental results an empirical factor which can be determined by the curve fitting method is necessary for all these models.
Tensile strength: The level of interfacial interaction was assessed by using the proposed predictive model of Pukanszky et al. [27-29] the model was chosen to study the relative change in the tensile strength of the PEEK/PEK/BT and PEEK/PES/BT nanocomposites to that of optimized blends of PEEK/PEK and PEEK/PES as matrix, respectively, with the variation of dispersed phase. The values of adhesion parameter, Bσ (calculated using Pukanszky model and experimental results) are shown in the Figure 1. The Figure shows that the interfacial adhesion increases up to 4wt% of filler loading and then decreases at higher filler content in both PEEK/PEK/BT and PEEK/PES/BT nanocomposites. This happened because at lower filler content, on an average, the fillers tend to improve the interfacial adhesion.
Figure 1:The change in adhesion parameter (Bσ) of PEEK/PEK/BT (■) and PEEK/PES/BT (●) nanocomposites against the nano-filler loading (wt%).
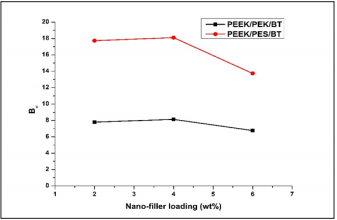
But at higher loading, the specific surface area of the nanofiller decreases due to the agglomeration of the nanoparticles. As a result, sharp decrease in the adhesion parameter observed because of lower interfacial interaction. The tensile strength is also affected by size of the dispersed phase of the filled system. The decrease in particle size increases the tensile strength due to the increase in interfaces. The increase in the interfacial area provides more effective interfacial interaction which is considered as one of the most important factors.
The dependence of flaw size of the material is related to the particle size. The stress field is independent of particle size near a particle. But with the increase of particle size of the dispersed phase the volume of the dispersing phase that experience stress concentration increased. So, there is a high probability of finding the large flaw with the increase in particle size. A cavity production equal to its own size of dispersed particle acts as an inherent flaw leading to the poor particle-matrix interaction. Hence the effect of particle size on the interfacial interaction directly governs the strength.
Similarly shape of the nano-filler is also expected to be an important factor for determining the tensile strength of nanocomposites. The weakening of strength due to high stress concentration along with the size effect comes from the irregular shaped inclusion. However, with the inclusions containing the sharp corners and the rounded cracks, stress becomes less severe.
Elongation at break: The relative elongation at break of both PEEK/PEK/BT and PEEK/PES/BT nanocomposites are shown in shown in Figure 2. The elongation at break was found to decrease in PEEK/PEK/BT nanocomposites while the same was observed to increase in PEEK/PES/BT nanocomposites. The decrease in elongation at break in PEEK/PEK/BT nanocomposites was due to deformation of nano filler which is much less than that of optimized crystalline polymer blends used as matrix. The filler forces the crystalline matrix to deform at higher rate than the overall deformation expected in the composites. But the elongation at break was found to increase in PEEK/PES/BT nanocomposites due to withstand of large deformations of nanocomposites with possible microvoid formation along with the probable detachment of the little lower crystalline polymer matrix and the nanoparticles loading up to 4wt% [37]. At higher loading i.e. 6wt%, voids are so numerous, large and sufficiently close to each other together that they coalesce, consequencing catastrophic macroscopic failure or fracture of material at the weak strains and the stresses [38].
Figure 2:Variation of relative elongation at break, εc/εm, of PEEK/PEK/BT (■) and PEEK/PES/BT (●) nanocomposites against the nano-filler loading (wt %).
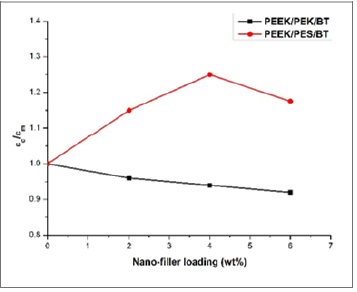
The percolation theory [25,30] can also be applied to explain the observed increase in elongation at break up to 4wt% and the decrease of the same at 6wt% loading of BT nano-filler. As per the percolation concept, both the dispersed particle and the interfacial region jointly act as a percolation cluster. Therefore, these percolation clusters are well-separated and disconnected from each other at lower loading of the dispersed phase.
At higher loading of the dispersed phase, percolation clusters interact due to the increased volume of the interfacial layers. Further increase in loading of the dispersed phase the interfacial layers overlap due to agglomeration. In consequence of this, the material fracture occurs at the lower strains and the stresses.
Thermal properties
The thermal behaviour of PEEK/PEK/BT and PEEK/PES/ BT nanocomposites was studied using DSC. The glass transition temperature and melting temperature of both the composites are shown in Figure 3(a) & (b). It was found that there is no change in the glass transition temperature (Tg ) of the PEEK/PEK/BT nanocomposites. However, the same was found to increase in PEEK/PES/BT nanocomposites. The marginal increase in Tg was found due to close packing of materials, dispersion of nanoparticles and heterogeneous nucleation. The improvement of the tensile modulus might be attributed due to the good adhesion of matrix and nanoparticles for which the segmental motion of matrix gets restricted [22]. In consequence of this Tg was found to increase marginally. The Tg obtained from DSC results were also verified by MDSC and the results were almost same (not shown). The marginal increase of Tg can also be explained by change in the thermal conductivity after adding BT. At lower concentration of BT, dispersion of nanoparticles is uniform. So, the nanocomposites are having the higher interface volume. The thermal conductivity of nanocomposite becomes relatively lower because of the presence of higher interfaces. However, at higher BT concentration when the interfaces are overlapping, the thermal conductivity usually does not go down further due to the agglomeration of the nanoparticles. Hence, the increase in Tg does not found after certain percentage of BT nanoparticles concentration of in the fabricated nanocomposites.
Figure 3:Glass transition temperature [3(a)] and melting temperature of PEEK/PEK/BT (●) and PEEK/PES/BT (■) nanocomposites against the nano-filler loading (wt %).
The melting temperatures were found in the typical range of 342- 345 oC for both PEEK/PEK/BT and PEEK/PES/BT nanocomposites. There are many factors involved with addition of the nanoparticles on crystallisation kinetics; few of them counteract each other, as a result, the resultant effect becomes obscure sometimes. As for example, the heterogeneous nucleation of both PEEK/PES and PEEK/PEK on the interface of nanoparticle might increase the crystallization temperature. But, the obstacle effect due to nanoparticles on the PEEK, PES and PEK chain mobility would decrease the crystallisation temperature [34]. Figure 4 is showing the peak crystallization temperature [4(a)] and Crystallinity [4(b)] of PEEK/PEK/BT (●) and PEEK/PES/BT (■) nanocomposites.
Figure 4:Peak crystallization temperature [4(a)] and Crystallinity [4(b)] of PEEK/PEK/BT (●) and PEEK/PES/BT (■) nanocomposites against the nano-filler loading (wt %).

From DSC diagrams, the percentage of crystallinity (Xc) of different nanocomposites were estimated by relating heat of fusion of infinitely thick PEEK crystal, ΔHf0, from the equation (12) as of following [39].

Where ΔHf0 is 130J/g approx., and Wpolymer is the weight fraction of the polymer matrix [40]. The crystallinity fraction was found to decrease marginally in PEEK/PEK/BT nanocomposites due to the lower mobility of the polymer chains when nanoparticle content was increased gradually [34]. Another reason for decrease in the crystallinity was disturbance of alignment of the crystalline portion due to presence of nanoparticles. The crystallinity fraction of PEEK/ PES/BT nanocomposites was found to decrease marginally at 2wt% loading when compared with crystallinity of the neat blend. This decrease of crystallinity was due to lower mobility of the polymer chains as explained above [34]. However, the same was found to increase in the presence of increasing BT nanoparticles content. It happened due to heterogeneous nucleation on the surface of the nanoparticles and due to the phase segregation. Hence, the overall crystallinity value of PEEK/PES/BT nanocomposites was found very close to that of the neat blend of PEEK/PES. So, by closer scrutinizing of DSC curves, it was observed that crystallisation temperature and the crystallinity of PEEK/PEK/BT and PEEK/PES/ BT nanocomposites were affected by the content of nanoparticles, while the melting point was found almost unchanged.
Phase morphology
The phase morphology of all blends and the nanocomposites was performed with the fractured surfaces of samples obtained from the impact test using SEM. Figure 5 is showing the micrographs of PEEK/PEK and PEEK/PES optimized blends. The blend of PEEK/PEK [Figure 5(a)] exhibits a homogeneous structure and also indicating miscibility of the blend system. The miscibility of PEEK/ PEK blend, we have already published in our previous paper [41]. The SEM image of PEEK/PEK blend is indicating homogeneous structure free of any separated domains at the obtainable resolution of SEM.
n the other hand, the blend of PEEK/PES [Figure 5(b)] exhibits a heterogeneous structure and indicating immiscibility of the blend system. The heterogeneous structure of phase separated domains is clearly visible in SEM micrograph of PEEK/PES blend system.
Figure 5:Micrographs of PEEK/PEK and PEEK/PES blends.
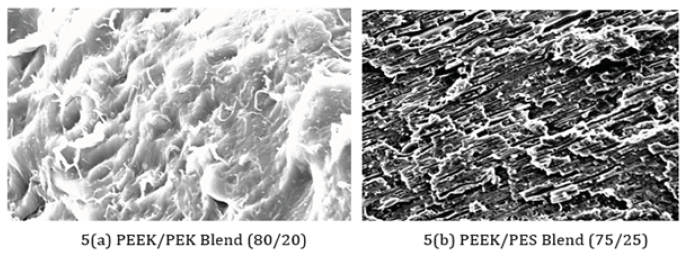
Figure 6:Micrographs of PEEK/PEK/BT and PEEK/PES/BT nanocomposites.

The SEM image of PEEK/PEK/BT nanocomposite [Figure 6(a)] is showing good uniform dispersion of the BT nanoparticles in the nanocomposites. In the SEM images, the nanoparticles were found 100-300nm which are higher than the size (35-80nm) we have reported in the ‘Materials’ section. The reason for getting higher size of nanoparticles was the tendency of BT nanoparticles to agglomerate and formation of irregular shaped aggregates with large (100-300nm) of large size [42]. This agglomeration was found to increase with the increasing content of nanoparticles.
It is an established fact that nanoparticle agglomerates in polymer matrix, as a result, reinforcing effect decreases. The SEM micrograph of PEEK/PES/BT nanocomposites is shown in Figure 6(b). It was found that the dispersion of nanoparticles is reasonably uniform in the nanocomposites. It was also observed that the segregation of nanoparticles was happened as shown in the Figure 6(b).
Conclusion
Two different sets of nanocomposites, PEEK/PEK/BT and PEEK/PES/BT were fabricated using the optimized blends of PEEK/PEK and PEEK/PES as matrix and barium titanate (BT) as nano-filler. The optimized blends were based on their thermal, mechanical and morphological properties.
The tensile strength and modulus were found to increase in both the nanocomposites due to reasonable interfacial adhesion in both sets of nanocomposites up to 4wt%. The decrease in both tensile strength and modulus were found for both nanocomposites at higher weight percentage i.e. 6wt%. However different results were observed in the case of elongation at break. The elongation at break was found to decrease in PEEK/PEK/BT nanocomposites while the same was observed to increase in PEEK/PES/BT nanocomposites.
The decrease in elongation at break in PEEK/PEK/BT nanocomposites was due to deformation of nano filler which is much less than that of optimized crystalline polymer blends used as matrix. The filler forces the crystalline matrix to deform at higher rate than the overall deformation expected in the composites. But the elongation at break was found to increase in PEEK/PES/ BT nanocomposites due to withstand of large deformations of nanocomposites with possible micro void formation along with the probable detachment of the little lower crystalline polymer matrix and the nanoparticles loading up to 4wt%.
At higher loading i.e. 6wt%, voids are so numerous, large and also sufficiently close to each other together that they coalesce, consequencing catastrophic macroscopic failure or fracture of material at the weak strains and the stresses. The same has also been explained with the concept of percolation theory. Different theoretical models can be used to evaluate the reliability of the experimental data. ‘Pukanszky model’ related to tensile strength and ‘Takayanagi’s model’ and ‘Guth and Smallwood model’ related to tensile modulus. From ‘Pukanszky model’, it was observed that tensile strength seemed to govern by the adhesion parameter, Bσ, which correlates the interfacial and the interphase interaction.
Acknowledgement
The authors are thankful to the competent authority of DMSRDE, Defence Research and Development Organization (DRDO) for giving permission to publish the article.
References
- Paul D, Newman S (1978) Polymer blends. Academic, New York, USA.
- Hull D, Clyne T (1996) An introduction to composite materials. Cambridge university press, UK.
- Utracki L (1989) Blends: Thermodynamics and rheology. Hanser, New York, USA.
- Olabis O (2012) Polymer-polymer miscibility. Elsevier, Netherlands.
- Remanan M, Kannan M, Rao RS, Bhowmik S, Varshney L, et al. (2017) Microstructure development, wear characteristics and kinetics of thermal decomposition of hybrid nanocomposites based on poly aryl ether ketone, boron carbide and multi walled carbon nanotubes. Journal of Inorganic and Organometallic Polymers and Materials, pp. 1-15.
- Zachariades AE, Porter RS (1988) High modulus polymers: approaches to design and development, Marcel Dekker, Inc, 270 Madison Ave, New York, New York 10016, USA.
- Hegazy ESA, Sasuga T, Nishii M, Seguchi T (1992) Irradiation effects on aromatic polymers: 1. Gas evolution by gamma irradiation. Polymer 33(14): 2897-2903.
- Thompson S, Farris R (1988) A novel method for crosslinking polyetheretherketone. Journal of applied polymer science 36(5): 1113-1120.
- Nishino T, Tada K, Nakamae K (1992) Elastic modulus of crystalline regions of poly (ether ketone), poly (ether ketone) and poly (p-phenylene sulphide). Polymer 33(4): 736-743.
- Knauer KM, Brust G, Carr M, Cardona RJ, Lichtenhan LD, et al. (2017) Rheological and crystallization enhancement in polyphenylene sulfide and polyetheretherketone POSS nanocomposites. Journal of Applied Polymer Science 134(7).
- Mandal S, Alam S (2013) Studies on crystallinity of PEEK/PEK/BT nanocomposites by using differential scanning calorimetry (DSC) technique and crystallinity effect on mechanical properties. Materials Research Innovations 17(6): 366-372.
- Nandan B, Kandpal L, Mathur G (2003) Poly (ether ketone)/poly (aryl ether sulphone) blends: thermal degradation behaviour. European Polymer Journal 39(1): 193-198.
- Mandal S, Alam S (2012) Studies on the mechanical, thermal, and morphological properties of poly (ether ketone)/poly (ether sulfone)/barium titanate nanocomposites: Correlation of experimental results with theoretical predictive models. Journal of Applied Polymer Science 126(2): 724-733.
- Liu L, Xiao L, Li M, Zhang X, Chang Y, et al. (2016) Effect of hexagonal boron nitride on high-performance polyether ether ketone composites. Colloid and Polymer Science 294(1): 127-133.
- Rivière L, Lonjon A, Dantras E, Lacabanne C, Olivier P, Gleizes NR (2016) Silver fillers aspect ratio influence on electrical and thermal conductivity in PEEK/Ag nanocomposites. European Polymer Journal 85: 115-125.
- Wang N, Yang Z, Wang Y, Thummavichai K, Xia Y, et al. (2017) Interface and properties of inorganic fullerene tungsten sulphide nanoparticle reinforced poly (ether ether ketone) nanocomposites. Results in Physics 7: 2417-2424.
- Kaelble DH (1979) Polymer Composite Reliability.
- Pecharroman C, Esteban‐Betegon F, Bartolome JF, Lopez‐Esteban S, Moya JS (2001) New percolative BaTiO3-Ni composites with a high and frequency‐independent dielectric constant (ϵr≈80000). Advanced Materials 13(20): 1541-1544.
- (2002) ASTMD 638 Standard test method for tensile properties of plastics.
- Guth E (1945) Theory of filler reinforcement. Journal of applied physics 16(1): 20-25.
- Ahmed S, Jones F (1990) A review of particulate reinforcement theories for polymer composites. Journal of Materials Science 25(12): 4933-4942.
- Goyal R, Tiwari A, Negi Y (2011) Role of interface on dynamic modulus of high‐performance poly (ether ketone)/ceramic composites. Journal of Applied Polymer Science 121(1): 436-444.
- Som T, Karmakar B (2009) Enhancement of Er 3+ upconverted luminescence in Er 3+: Au-antimony glass dichroic nanocomposites containing hexagonal Au nanoparticles. JOSA B 26(12): B21-B27.
- Takayanagi M, Uemura S, Minami S (1964) Application of equivalent model method to dynamic rheo‐optical properties of crystalline polymer. Journal of Polymer Science: Polymer Symposia, Wiley Online Library, pp. 113-122.
- Ji XL, Jing JK, Jiang W, Jiang BZ (2002) Tensile modulus of polymer nanocomposites. Polymer Engineering & Science 42(5): 983-993.
- Hashin Z, Shtrikman S (1963) A variational approach to the theory of the elastic behavior of multiphase materials. Journal of the Mechanics and Physics of Solids 11(2): 127-140.
- Pukánszky B, Fekete E (1999) Adhesion and surface modification. Mineral fillers in thermoplastics I, pp. 109-153.
- Ishida H (1988) Interfaces in polymer, ceramic, and metal matrix composites. Proceedings of the Second International Conference on Composite Interfaces (ICCI-II), Cleveland, New York, USA.
- Pukanszky B, VöröS G (1993) Mechanism of interfacial interactions in particulate filled composites. Composite Interfaces 1(5): 411-427.
- Nicolais L, Narkis M (1971) Stress‐strain behavior of styrene‐acrylonitrile/glass bead composites in the glassy region. Polymer Engineering & Science 11(3): 194-199.
- Rong MZ, Zhang MQ, Pan SL, Lehmann B, Friedrich K (2004) Analysis of the interfacial interactions in polypropylene/silica nanocomposites. Polymer International 53(2): 176-183.
- Agarwal BD, Broutman LJ (1990) Analysis and performance of fiber composites.
- Maiti S, Das R (2005) Mechanical properties of impact i-PP/CSM rubber blends. International Journal of Polymeric Materials 54(6): 467-482.
- Kuo M, Tsai C, Huang J, Chen M (2005) PEEK composites reinforced by nano-sized SiO2 and Al2O3 Materials Chemistry and Physics 90(1): 185-195.
- Hashin Z (1963) Theory of mechanical behavior of heterogeneous media. Pennsylvania Univ Philadelphia Towne School of Civil and Mechanical Engineering.
- Hill R (1963) Elastic properties of reinforced solids: some theoretical principles. Journal of the Mechanics and Physics of Solids 11(5): 357-372.
- McNally T, Murphy WR, Lew CY, Turner RJ, Brennan GP (2003) Polyamide-12 layered silicate nanocomposites by melt blending. Polymer 44(9): 2761-2772.
- Hocine NA, Médéric P, Aubry T (2008) Mechanical properties of polyamide-12 layered silicate nanocomposites and their relations with structure. Polymer Testing 27(3): 330-339.
- Sandler J, Werner P, Shaffer MS, Demchuk V, Altstädt V, et al. (2002) Carbon-nanofibre-reinforced poly (ether ketone) composites. Composites Part A: Applied Science and Manufacturing 33(8): 1033-1039.
- Wei CL, Chen M, Yu FE (2003) Temperature modulated DSC and DSC studies on the origin of double melting peaks in poly (ether ketone). Polymer 44(26): 8185-8193.
- Mandal S, Alam S (2010) Mechanical properties of poly (ether ketone)/poly (ether ketone) blends: Use of simple models relating normalized tensile parameters. Journal of Applied Polymer Science 117(2): 849-856.
- Lee BI, Wang X, Kwon SJ, Maie H, Kota R, et al. (2006) Synthesis of high tetragonality nanoparticle BaTiO3. Microelectronic Engineering 83(3): 463-470.
© 2019 Subhash Mandal. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






