Permanent Magnets Elaboration from BaFe₁₂O₁₉ Hexaferrite Material: Simulation and Prototype

Many technological advances have become possible only after the development of extremely powerful permanent magnets in very different shapes and sizes. Today, ferromagnetic materials have very high energy densities. Families of permanent magnets with various magnetic and mechanical properties, may be suitable for a numerous application, particularly for the realization of DC devices [1] or synchronous machines [2]. The existence of a magnetic field in the absence of current opened the door widely front of the realization of sensors, like proximity sensors, NMR and MRI [3-5]. The nature of the materials composing the permanent magnet has a significant effect on its power. Permanent magnets almost always contain atoms of at least one of the following chemical elements: iron, cobalt, nickel or the rare earth family such as scandium, yttrium and lanthanides or neodymium and samarium. These kinds of permanent magnets have a such as those based on neodymium which are known as NdFeB magnets (Nd₂Fe₁₄B) [6], as known the magnets containing rare earths have a large coercive field Hc, but the main disadvantage is that it decreases when the temperature increases, contrary to the hexagonal ferrites which increases with the temperature. In addition, hexaferrites are inexpensive and easy to manufacture, unlike rare earth magnets.

The Hard ferrites or hexaferrites is the first permanent magnets which constitutes from oxides of hexagonal structure based on barium or strontium A(Fe₁₂O₁₉), A=Ba, Sr or Pb. The crystal structure and behaviour of atoms at the sublattice sites of BaFe₁₂O₁₉ can be understood by Raman and Mössbauer spectroscopic techniques. BaFe₁₂O₁₉ belongs to the class of magnetoplumbite type materials and has a mixed spinel (S and S* blocks) and hexagonal (barium containing R and R* blocks) closed-packed structure, with Ba²⁺ atom substituting for an O^2- atom, and iron ion occupying interstices (Figure 1).

The arrows on Fe ions represent the direction of spin polarization. The unit cell contains a total of 38 O^2- ions, 2 Ba²⁺ ions, and 24 Fe³⁺ ions. Fe³⁺ ions in 12k, 2a, and 2b sites (16 total per unit cell) have their spins up, while the Fe³⁺ ions in 4f1 and 4f₂ sites (8 total per unit cell) have their spins down, which results in a net total of 8 spins up. The R and S subunits shown have chemical formulae R=(Ba²⁺Fe³⁺6O^2-₁₁)2- and S= (Fe³⁺8O^2-₈)²⁺ [7,8]. The hexaferrite BaFe₁₂O₁₉ is characterized by a Curie temperature between 730K and 740K [9], and a very high uniaxial magnetocrystalline anisotropy of K=3.3×10⁵Jcm^-3 [10]. However, a major disadvantage is the evolution of magnetization with temperature [9], therefore these magnets have relatively low values of magnetization at room temperature. In this paper, we study the magnetic properties behavior of hexaferrite material BaFe₁₂O₁₉ as a function of the external magnetic field and under the influence of temperature for different magnetic field directions in order to analyze the effect of magnetocrystalline anisotropy energy on the saturation magnetization using the simulation method by Mumax3 code [11]. The aim is to innovate a prototype proposal in order to elaborate a permanent magnet from BaFe₁₂O₁₉ hexaferrite material with special experimental equipment to generate an adjustable strong field which allows us to study the evolution of the saturation magnetization.

Figure 1:Schematic structure of the hexaferrite BaFe₁₂O₁₉[7].

The application of an external magnetic field H results in the introduction of a new energy term which modifies the primitive energy equilibrium state of the hexaferrite material BaFe₁₂O₁₉ to create a new configuration. At first, there is an increase in some areas to the detriment of their neighbors through the walls motion. For the weak fields, this displacement is still reversible (phase 1, Figure 2). When the fields are strong, the displacements become irreversible: the domains become less numerous and the direction of the spontaneous magnetization is gradually oriented in the direction of the field H (phase 2, Figure 2). For the important fields, the walls disappear, we obtain the magnetic saturation of the ferrite material Ms=0.038T with a saturation field of μ₀H_s=1.5T ((phase 3, Figure 2).

Figure 2:First magnetization curve of ferrite material.

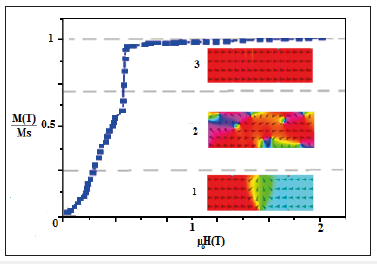
When the field decreases, the magnetic domains begin to orient themselves and to take the easiest orientation close to the applied field (curve AB Figure 3). During the field decreasing, the magnetoelastic energy of the crystal becomes very large, for μ₀H=0A/m this translated by a remnant magnetization of Mr=0.036T, for the coercive field measurement it is necessary to increase the magnetic field negatively until the magnetization value becomes equals zero which corresponds to a coercive field value of |μ₀H_s|=0.47T. When the field keep up to decrease, the magnetization reaches a minimum value of Ms=0.0380T (CD curve). As shown in Figure 3 the grey area inside the hysteresis loop represents the energy expended per unit volume of the ferrite material.

Figure 3:Magnetic hysteresis loop of the ferrite material.

Effect of temperature on magnetization behavior during saturation

We studied the behavior of BaFe₁₂O₁₉ hexaferrite material during a static magnetic field polarization μ₀H, following the easyaxis to magnetized for two values of the temperature. In Figure 4 & 5, hexaferrite material simulation results are presented and partially illustrate the non-linear evolution of the parameters as for magnetic hysteresis loop, remnant magnetization, saturation magnetization, coercive field, as a function of the external magnetic field for two selected values of temperature T=298K and T=358K. First, we simulated the evolution of the magnetization with a temperature of T=298K. In this case, the magnetization reaches the saturation very quickly with a value of the magnetization up to 0.0380T and a magnetic field of μ₀H_s= 1.5T, and that due to the anisotropy energy which is at its minimum in this axis. On the other hand, when the value of the temperature is increased to T=358K the behavior of the magnetization is changed, the moments find it difficult to orient themselves and consequently the magnetization takes another path with a magnetization value of M2=0.034 T which is smaller than the saturation magnetization. To reach the same value of the saturation magnetization Ms=0.0380T, it is necessary to supply more energy by applying strong magnetic fields.

Figure 4:Evolution of first magnetization of ferrite material for different values of temperature.

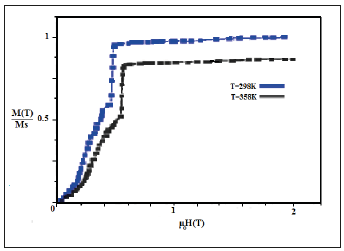
Figure 5:Evolution of the hysteresis loop of a ferrite material under different temperature values.

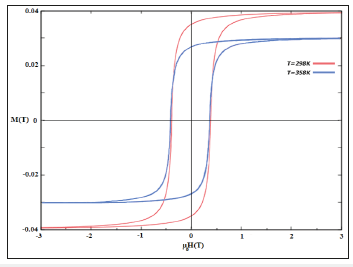
As seen before the increase in temperature has a drastically negative influence on the saturation value of hexaferrite material but to study the effect of the temperature on remnant magnetization and coercive field, it is necessary simulated the magnetization evolution on the whole hysteresis loop for the two values of the temperature T=298K and T=358K (Figure 5).

At room temperature, we triggered the saturation at Ms=0.0380T with an external magnetic field of μ₀H_s= 1.5T, then we slowly decreased the external field to the zero and thanks to the static losses of the energy and the magnetocrystalline anisotropy affect, the trajectory of the magnetization begins to deviate to a remnant magnetization of Mr1=0.036T. We continued to decrease the external field down to the coercive field value of |μ₀H_c1|=0.47T. At a temperature of T=358K and for a field of μ₀H_s=1.5T, the magnetization reaches M2=0.3T which is smaller than Ms and consequently a remanent magnetization of Mr2=0.25T < Mr1, but against the coercive field behavior remains almost the same |μ₀H_c2|=|μ₀H_c1|=0.47T because the variation of the temperature is not enough to show the difference, while for a much higher temperature the coercive field μ₀H_c2 becomes inferior to μ₀H_c1.

Magnetocrystalline anisotropy effect on the hysteresis loop

The distance between two neighboring atoms depends on their relative position in the crystal lattice, because of to the exchange energy between the different atoms, so it takes more or less energy to magnetize a material in certain directions, this comes back to define the directions of the easy-axis and the hard-axis of magnetization. In figure 1, we have shown the axes of the hexaferrite with θ and φ being the angles defined in polar coordinates where the axis [001] is the easy-axis of magnetization, it is parallel with z and the axes [100] and [110] are the hard-axis of magnetization with a great magnetocrystalline energy.

This energy is described by the free energy equation [12]:

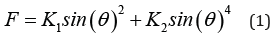
For the fields applied along the hard-axis, the free energy density is written as:

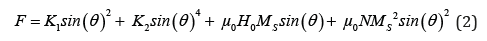
The term before the last, is the term Zeeman, and the last term expresses the energy of the demagnetizing field.

The solution that is imposed when the field is sufficiently small is given as:

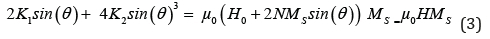
With sin(θ)=M/MS we obtain:

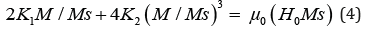
From this equation we find that the magnetic susceptibility in the weak field is:

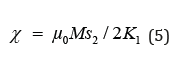
The saturation is triggered (M=Ms) through certain anisotropy fields HA larger than the saturation field and which is given by the equation:

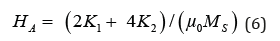
We have studied the effect of magnetocrystalline anisotropy on the behavior of the hysteresis loop parameters of ferrite materials including saturation magnetization, saturation field, coercive field in two magnetic field directions.

When the field is applied along the easy-axis of magnetization (Figure 6), the free displacement of the walls leads to the disappearance of the domains, as soon as the applied field is greater than Ms/3, all the magnetic moments are orienting themselves to the magnetic field direction and consequently the macroscopic magnetization is then equal to the microscopic magnetization Ms=0.0380T with a remnant magnetization of Mr=0.036T. When the field is applied on the hard-axis of magnetization, no domain being favored therefore their volume does not change. The magnetization of each of them turns at the same angle by reason of the anisotropy energy which is very important in this axis. For the saturation field of μ₀H_s=1.5T, we reach a magnetization of M=0.0372T less than the saturation magnetization Ms, to arrive at the same value of the saturation magnetization, it is necessary to apply an external field called anisotropy field HA (see Eq. 6), as shown in the Figure 6 this field equal to μ₀H_A=1.7T where it is much larger than the saturation field in order to overcome the anisotropy energy on this axis.

Figure 6:Evolution of the hysteresis loop of a ferrite material by two directions of magnetic fields.

At zero magnetic field, we reach a remnant magnetization of Mr=0.022T which is smaller than remnant magnetization on the easy-axis of magnetization. From the curve M(H) along the hardaxis and the Eq (5), we have specified the constants of anisotropy K1 and K2 of the hexaferrite material. the susceptibility in weak field equal to χ=1.7×10-5 therefore, the constant of anisotropy is K1=3.4×10⁵J/cm₃ and thanks to these values, we have found through the Eq (6) that the constant of anisotropy K2 equal to -1.6×10⁵J/ cm₃. We point out that these values are in agreement with the experimental results [10].

Experimental results

In this part, we start to elaborate a permanent magnet from BaFe₁₂O₁₉ hexaferrite material by a prototype proposal using experimental equipment shown in Figure 7 for the creation of an intense magnetic field. We placed the sample between the poles of a very powerful electromagnet oriented in the desired direction of magnetization. The electromagnet is then powered with direct current for a certain time. The magnetic force aligns the magnetic domains of the material towards a single domain to make it into a strong permanent magnet. The sample is in the shape of a metal rod of two round sections at the end. The objective of having two sections is that the first is of a positive magnetic field which represents the northern part of the permanent magnet and the second section represents the southern part. The best structure is when the surface of the ends of material represented by parallel surfaces.

Figure 7:Experimental equipment and the sample of Hexaferrite material.

First, we put our sample between the poles, then we increased a little bit the magnetic field to the value of μ₀H_s=1.5T by increasing the current and at the same time for each field value we measured the magnetization of the hexaferrite sample up to the saturation magnetization value of Ms=0.0378T.

After, we slowly decreased the magnetic field H until the value of μ₀H=0T, then we measured the remnant magnetization Mr=0.035T. We have further reduced the magnetic field to the value where the magnetization is zero and therefore getting the coercive field of hexaferrite material. We have negatively increased the field up to the value of μ₀H_s=1.5T this tends to align the magnetic moments in the same direction and thus reach the negative saturation Ms= 0.0378T.

Strong magnetic fields greater than 1.5T are required to magnetize the hexaferrite material of BaFe₁₂O₁₉ in order to achieve the best performance of magnetic materials. In this paper, we used the simulation and experimental measurements to study the magnetization dynamics through the first curve of magnetization and the magnetic Hysteresis Loop, in order to specify the main characteristics of hexaferrite such as saturation magnetization and coercivity field where the comparison between measured and simulated data showed a good agreement. This study is motivated by the many applications of permanent magnets and is conducted to evaluate the magnetization performances of hexaferrite magnet. This kind of magnets are suitable for rotors and gives, thanks to their anisotropic magnetizing property which is an improved quality in designing new engines.

1. Hameyer K, Belmans RJM (1996) IEEE T Ind Electron 43(2): 247-255.
2. Jahns TM, Kliman GB, Neumann TW (1986) J IEEE T Ind Appl 4: 738-747.
3. Wegener R, Senicar F, Junge C, Soter S (2018) 7th International conference on power electronics and drive systems PEDS 2017, Bangkok, Thailand, 27-30 November 2007. Institute of Electrical and Electronics Engineers: Piscataway, New Jersey, USA, pp. 1367-1371.
4. Hugona C, Aguiar PM, Aubert G, Sakellariou D (2010) J Cr Chim 4: 388- 393.
5. Zijlstra H (1985) Philips J Res 40(5): 259-288.
6. Pinkerton FE, Van WDJ (1986) J Appl Phys 60(10): 3685.
7. Pardavi HM (2000) J Magn Mater 1: 171-183.
8. Smit J, Wijn HPJ (1959) Ferrites, (1st edn), Eindhoven: Netherland.
9. Lommel JM, Shirkt BT, Buessem WR (1969) J Appl Phys 40(3): 1294.
10. McCurrie RA, Jackson S (1987) J Appl Phys 2: 62.
11. Vansteenkiste A, Jonathan L, Mykola K, Mathias H, Felipe GS, et al. (2014) J Aid Adv 4: 107133.
12. Du Tremolet De Lacheisserie E (2001) In: Magnétisme I, Fondements, (1st edn), Les Ulis, France, pp. 101-113.