- Submissions

Full Text
Research & Development in Material Science
Short Notice: The Integration of Variables Method
José Arzola-Ruiz*
Technological University of Havana, Cuba
*Corresponding author:José Arzola- Ruiz, Technological University of Havana, Cuba
Submission: June 21, 2019;Published: June 25, 2019

ISSN: 2576-8840 Volume11 Issue2
Opinion
The concept of the Integration of Variables Method is linked to the evolution of any quantity of codes helped by any set of operators to upgrade corresponding solutions populations. It general features are illustrated in Figure 1: The possible solution variants are coded in one or more variables-codes, it is generated, according to a procedure characteristic for each particular application of the method, a set of n solutions close to the optimal one. Particularly, different procedures which are characteristic for different classes of Mathematical Programming methods applied to the solution codes could be used, with selected search environments in a random, deterministic or combined way. Each particular procedure of generation and upgrading populations has to do with a concrete application variant of the method.
Figure 1:General outline of the integration of variable methods.
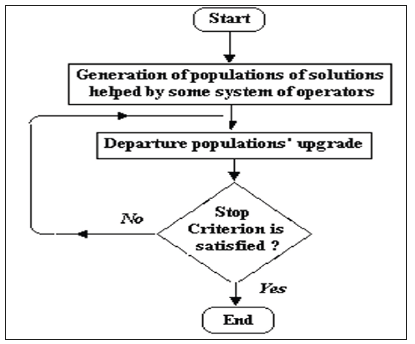
So, the application of any heuristic derived from the Integration of Variables Method requires the definition of the following problems: a coding system for the possible solutions representation of the studied problem, a method for creating one or various initial population(s), a quality (fitness) function that allows ordering the codes according the objective function values, operators that allow the altering of the composition of solutions codes in the successive populations, stop criteria and parameters values required by the algorithm used (population’s size, probabilities associated with the application of certain operators, etc.).
Despite the general acceptance received in the last decades by other metaheuristic methods in many particular cases, difficulties have appeared in its application to optimization problems due to the following causes: there is no guarantee of obtaining the global optimal solution although generally have the tendency to do so. This tendency is frequently reduced when there is a loss of population diversity, which can lead to final populations of low quality and poor diversity, slowness of searching process in comparison with other methods, etc.
The author had developed some algorithms in the frame of the Integrations of Variables method that could in occasions overcome mentioned difficulties, particularly, increasing the diversity of the solutions populations, close to the efficient ones, that facilitate the selection of the definitive solutions by deciders as a result of being able to choose between close by the objectives functions solutions but diverse for their characteristics what has been verified in numerous application researches.
Searching by random localization of the extreme of a function of a variable code
In Figure 2 the practical application of the Integration of variables method to the concrete case, when the searching procedure of local minima of a function of a variable code of possible solutions to the given discrete optimization task with random variation of search intervals for upgrading the successive solutions populations is illustrated.
Figure 2:Pseudocode of the localization of the extremes of a function of a variable code algorithm.

In the pseudocode shown in Figure 2, in each iteration it is carried out the search of the minimum of a function of a variable code (that constitute the values, in the decimal system of numeration, of the variable-code of the looked-for solution). The initial variable code values are generated aleatorily inside the interval of possible values of the solution variable code
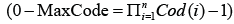 . Searching solutions is carried
out by the operator of the Localization of the minimum of the
function of one independent variable method. The quality function
Z could be interpreted in the same way that Genetic Algorithms
does, as fitness, and it could include the result of the calculation
of a penalty function for the no fulfillment of the restrictions. This
value is calculated by the generation and decoding of random
values inside the current search interval (CodMin, CodMax) that
decreases in each iteration by the elimination of the sub-interval
that doesn’t contain the best solution between the both generated.
In each localization iteration it is included in the population the
found solutions, while the population’s size is smaller than the
established one (CInd) or the population is upgraded in case it
already reached the established size. Once the foreseen precision
is reached the generation of random values process is restarted
to its initial values. The procedure continues until the number of
followed iterations without the population of solutions upgrading
(Noact) reaches a pre-established value (NoactMax).
Every current solution is decoded by the universal algorithm
shown in Figure 3. Every generated code x is decoded by the
algorithm shown in Figure 3.
. Searching solutions is carried
out by the operator of the Localization of the minimum of the
function of one independent variable method. The quality function
Z could be interpreted in the same way that Genetic Algorithms
does, as fitness, and it could include the result of the calculation
of a penalty function for the no fulfillment of the restrictions. This
value is calculated by the generation and decoding of random
values inside the current search interval (CodMin, CodMax) that
decreases in each iteration by the elimination of the sub-interval
that doesn’t contain the best solution between the both generated.
In each localization iteration it is included in the population the
found solutions, while the population’s size is smaller than the
established one (CInd) or the population is upgraded in case it
already reached the established size. Once the foreseen precision
is reached the generation of random values process is restarted
to its initial values. The procedure continues until the number of
followed iterations without the population of solutions upgrading
(Noact) reaches a pre-established value (NoactMax).
Every current solution is decoded by the universal algorithm
shown in Figure 3. Every generated code x is decoded by the
algorithm shown in Figure 3.
Figure 3:Decoding x codes algorithm.
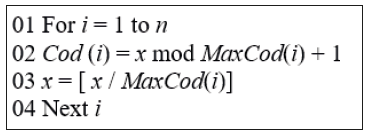
© 2019 José Arzola-Ruiz . This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






