Definition of the Period of Big Fluctuations of the Pendulum (To 90o)

Pendulum as an element of means of measuring time has been known for centuries. Before the invention of quartz pendulums are used in the manufacture of the most accurate astronomical clocks and chronometers. Until now, the pendulum is used as a measuring apparatus at geophysical tests. The problem of determining the local gravity (gravitational acceleration) is very important in various fields of human activity.

Topography can be set by various methods, including space triangulation methods. Seismic methods can be set (although quite inaccurately) the distribution layers of different densities. However, the exact value of the gravitational acceleration at a particular point of the Earth can be determined only by using a pendulum as a means of measurement. It is worth mentioning that in the experiments to establish the gravitational constant in the law of universal gravitation (the experience of Cavendish) used pendulums. Also indispensable when the pendulum demonstrating the Earth’s rotation (Foucault pendulum).

Driving pendulum is widely used in devices for the impact test such as copra, crane sector, the dynamic damping devices, handling and transport facilities, in research on biomechanics (timing gymnastics), and others. Research time oscillation of the pendulum mass and are traditionally used in educational courses of engineering educational institutions and universities, for example, in the demonstration test.

Meanwhile, the problem of determining the period of large swings of the pendulum (20 degrees) is still in the discussion. Bibliography on the analytical solution of this problem mainly concerns the works [1-4]. Formulation of the problem. The systematic study of the question of the period of oscillation of the pendulum begins to work Huygens described in his memoir «Pendulum clock» [1] in 1673. In this memoir Christiaan Huygens is a simple method for calculating the length of the pendulum for the required period. If small oscillations of a pendulum Huygens [1] proves its findings oscillation periods, which devotes an entire chapter of the memoir Huygens, for the wide-angle Huygens [1] only expressed that «On the other hand, it is possible to calculate the ratio of the periods under different arcs span, based on strong principles and with any accuracy. You can, for example, show that the time during which the pendulum takes a quarter of a circle, dates back to the fall of a very small arc as 34:29. This difference oscillation periods in any case is not explained by the air resistance, as some, but it follows from the nature and properties of the motion range «[1, c. 19]. At the same time, Huygens gives a very exact relationship: «This definition is very precisely 34:29 = 1,172. The true value is equal to 1,180, m. E. The error is only 0.8%. German commentators Huygens [1] Geksher and Jettingen note that Huygens, does not specify how he found the result, and that a complete analytical solution of the problem was only Elvius in 1734 with the help of elliptic integrals «[1, c. 317].

Huygens [1] only mentions that he knows how to calculate the period of large swings of the pendulum, but did not disclose his knowledge on the subject. Only after 60 years, scientists have been able to find a method of solving this problem and check calculations of Huygens [1]. Characteristically, Elvius managed to solve the problem only by elliptic integrals.

A complete study of elliptic functions and their application to mechanics has taken Appel [3], published (with Lacour [2]) in 1897. The 1897 monograph Appel [2] strictly proves that the solution of the differential equation of motion of the pendulum for large angles reduced to elliptic integrals. Solution of the problem of determining the period of large swings of the pendulum Appel [2] lead in the three-volume edition of Traite mecanique rationnelle [2], which went through several editions in French, often translated into other languages in Vol. H., And Russian. In Russian labor P. Appel translated twice in 1911 and 1960.

Publication 1960 transfer Malkin, edited by SM Targ, contains two volumes of Appel [3]. In this work we solve the large fluctuations of the pendulum [3, c. 515], which in one form or another be found in modern literature.

According Adlaj [4] many (if not all) of authoritative sources on mechanics now refer to elliptical solve this problem [4]. Thus, method of solving the problem of determining the period of oscillation of the pendulum at large deviations by integrating the differential equations of motion leads to elliptic integrals. As is known, elliptic integrals do not provide a solution in elementary functions, and only allow an approximate solution by iteration.

Discussion of alternative ways of solving the problem

It offers another method of solving this problem. If the integration of the differential equations of motion of the second order does not allow to find a final solution in elementary functions, it is interesting to solve the problem of bypassing the use of differential equations. Such a method is. The differential equation gives the instantaneous velocity in each time period, but in practice, the metrological tasks often enough to find the full period of oscillation of the pendulum. If you give up the need to have the exact value of the instantaneous velocity of the pendulum and use the average speed over the period of a pendulum, the need for differential equations disappears.

If you need to know for what period the pendulum will cover the distance from the starting point as well, to the end point b, it is not necessary to know how fast the pendulum held separate areas within the interval ab, and what was the instantaneous velocity at any given point in time.

By the mean value theorem in integral calculus, if the function f (x) is integrable in the area ab, and at the site feature preserves the sign, there exists a value of f (c), that:

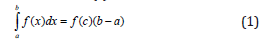
The consequence of this theorem is a formula (2) the average value of the integrated functions:

where c = f - the average value of the integral function.

If a function in the area ab, is everywhere positive, regardless of the type of functions, with the average value of the integral can be calculated without the need for integration. If we know the average speed of the oscillation period and the path traversed by the pendulum over the same period, it is possible to calculate the period of oscillation without the need for integration of differential equations of motion of simple algebraic operations.

The condition of the theorem on the integral average is the immutability of the sign function. The speed of the pendulum changes sign, in the first half-period of the sign is positive, the pendulum moves in one direction, while the second - a sign of the velocity is negative, the pendulum is moving in the opposite direction. Use of the mean-value theorem can be applied to half of the period of oscillation of the pendulum.

The rate in each half cycle, first increases, reaching a maximum at the passage of the point of equilibrium, i.e., acceleration is positive. In the second quarter of the period, the rate decreases, reaching zRDMS at the opposite point of maximum deviation, i.e., acceleration is negative. Pendulum oscillations are divided into four quarter periods, in each of which the variation is identical, except for the sign of speed and acceleration. It is enough to find the average rate of the pendulum in one quarter of the period, and the total value of the period obtained by multiplying the length of one quarter to four.

A method for finding the period of a pendulum in elementary functions

Figure 1:Physical pendulum.

We direct the y-axis down and compare the starting point of zRDMS ordinate value. We write the law of conservation of energy for a physical pendulum (Figure 1):

where m - mass of the body; g - acceleration of free fall; h - height of lifting the cm on the position of equilibrium; v - velocity of the cm motion.

We get:

Substituting in (4), we obtain the formula instantaneous velocity of the center of mass:

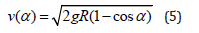
Meanwhile within 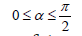function cos(α) decreases monotonically in the range of 1 at α = 0, because cos(0)=1, to 0 at 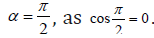According to formula (5), the maximum velocity should be the starting point αmax, and the equilibrium point α = 0 is the absolute minimum. To bring the situation into line with the boundary conditions necessary to apply the operation of normalization that the maximum speed corresponds to the equilibrium point. The operation, which will lead to the desired results - a shift of the reference point on the deflection angle. In this case, the equation (5) can be rewritten as:

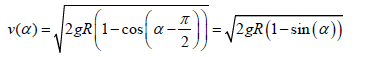
We find the mean integral value of the speed at the site of the first quarter of the period of oscillation of the pendulum from its initial position at the maximum deviation to the point of equilibrium (see. Fig.).

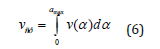
where v(α ) - - the instantaneous velocity of the center of mass; α - - The angle of deflection the cm pendulum. Substituting (5) into (6):

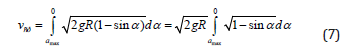
The problem is reduced to finding the integral:

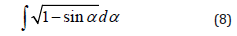
Change of variables

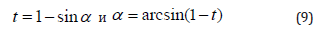
we get:

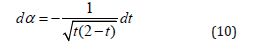
Substituting (9) and (10) to (8):

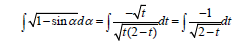
Change of variable z = 2 − t or t = 2 − z the problem reduces to the table integral:

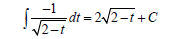
Substituting the values of f (8) we get:

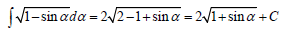
Using primitive integral, solve the problem of finding the average rate in the first quarter of the period of oscillation of the pendulum. From (7) and (11) we have:

Finally:

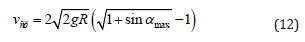
The last equation determines the value of the average rate of passage of the position of the maximum deviation to the equilibrium point. It should be noted that the conclusion of this equation has been made by the authors of this article in several ways.

Speed after the point of balance to the opposite position of the maximum will be mirrored, i.e., if in the first quarter of the swing of the pendulum accelerates from 0 to v_max, the next quarter of a reduced rate of mirror from v_max to 0. When reaching the second point of maximum deviation over the second quarter fluctuations. By virtue of the second half of the space is isotropic fluctuations (the third and fourth quarters) repeats the first half of the oscillation period. The expression (12) to determine the period of oscillation of the pendulum:

where T - period of oscillations; S - distance traveled; vср - average speed during the period.

The length of the central angleφ of the arc is defined by the formula:

I.e the passage of the pendulum arc with an angle ϕ equal to:

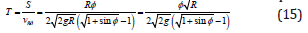
The path traversed for the full period, determined by the formula:

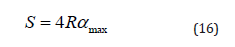
Here R - radius of the cm pendulum; α_max -The maximum deflection angle of the pendulum, radian; 4 - factor present in view of the fact that the product Rα_max defines the path traversed by ¼ of the oscillation period of the pendulum. Substituting in (13) equation (12) and (16) we obtain:

This is the period of small oscillations of a physical pendulum, provided that.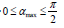

Here are the final results. If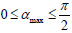 the period of large swings of the pendulum is determined by the formula (17):

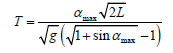
In this formula, instead of R (radius of swing of a pendulum) is given the value of L - length of the pendulum, as is customary in modern literature.

Despite the fact that Huygens in his treatise technique does not solve the problem for the big pendulum, however, it causes a specific figure. According to Huygens’s [1] attitude since the fall of the pendulum, starting from the corner,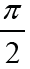the time of the fall of the small angle correlated as 34:29 [1, c. 19] or 1: 1.1724. In a footnote to the treatise Huygens [1] stated that the value obtained from the solution of elliptic integrals, still 1,180 [1, c. 317].

Compare with the solution obtained in this article. According to contemporary sources, the period of small oscillations of a pendulum:

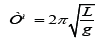
From this we can determine the time of fall of the pendulum, starting with a small angle of deflection, it will be equal to one quarter of the period of a pendulum, or:

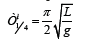
According to equation (18) the fall of the pendulum, since the angle 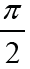equally

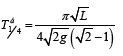
Find the ratio of:

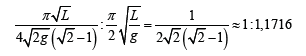
The resulting value is different from the value specified by Huygens 0.07%, and from solutions of elliptic integrals - 0.72%. The solution obtained in the order closer to the numerical value specified Huygens than to the solution of elliptic integrals, which is considered to be accurate.

The question remains how to determine the period of oscillation of the pendulum in the 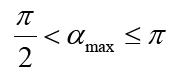. Solving this problem will be presented in the following article.

The scope of this article is a theoretical solution to the problem of determining the time of large fluctuations in the pendulum when the limit amplitude of small oscillations or methodologically impossible, for example, in experiments to determine the gravitational constant, or technologically difficult.

In the latter case, there is the following in mind: to provide a large oscillation periods provided that «small fluctuations» need to increase the length of the pendulum, as it is done for the Foucault pendulum in St. Isaac’s Cathedral (or similar). Removing restrictions on the deflection angle of the pendulum will significantly reduce the size of the device.

Of course, at the disposal of Metrology solutions are determining the period of large fluctuations using elliptic integrals, but these methods require high computing power, and proposed an analytical solution does not require it.

1. Huygens H (1951) Three memoir on mechanics. M USSR Academy of Sciences, Russia.
2. Appell P, Lacour E (1897) Principes de la Theorie des Fonctions Elliptiques et Applications. Gauthier-Villars, Paris, France.
3. Appel PA (1960) Theoretical mechanics.
4. Adlaj S. An eloquent formula for the perimeter of an ellipse. Notices of the AMS 59(8): 1096-1097.