- Submissions

Full Text
Research & Development in Material Science
Evidence of Ferromagnetism in the Diluted Magnetic Semiconductor CuGa1-xMnxTe2
José RF1,2*, Carlos Durante R1,3 and Jaime AC1
1 Departamento de Física, Venezuela
2 Escuela de Ing Industrial, Venezuela
3 Escuela de Ciencias Físicas y Matemáticas, Ecuador
*Corresponding author: José RF, Departamento de Física, Escuela de Ing Industrial, Venezuela
Submission: October 28, 2018; Published: November 30, 2018

ISSN: 2576-8840 Volume9 Issue2
Abstract
We report on experimental and theoretical evidence of a ferromagnetic phase in the diluted semiconductor CuGa1-xMnxTe2 using the Ferromagnetic
Resonance (FMR) technique. The FMR spectra were studied as functions of temperature (T) manganese concentration (x) and magnetic field orientation.
The samples were synthesized by direct fusion of the stoichiometric mixture of the elements, with Mn composition from x=0.05 to 0.25. The data were
interpreted in the framework of a phenomenological model for single domain uniaxial grains. The temperature variation of the resonance field shows a
critical point at about 230K, which is associated with a transition from the ferromagnetic to paramagnetic state. This behaviour is explained assuming
an effective magnetization following the exponential law 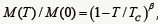 , with β≈0.40. The resonance field as a function of the field angle displays
a well-defined uniaxial symmetry at high Mn concentrations. This uniaxial field is Mn concentration dependent and is due to the formation of ovoid Mn
grains with G-factor greater than 3.0..
Keywords: Magnetic semiconductors; Magnetic anisotropies; Ferromagnetic resonance; Diluted ferromagnets
, with β≈0.40. The resonance field as a function of the field angle displays
a well-defined uniaxial symmetry at high Mn concentrations. This uniaxial field is Mn concentration dependent and is due to the formation of ovoid Mn
grains with G-factor greater than 3.0..
Keywords: Magnetic semiconductors; Magnetic anisotropies; Ferromagnetic resonance; Diluted ferromagnets
Introduction
Diluted magnetic semiconductors (DMS) are alloys in which a magnetic ion is randomly distributed into the solid host and have been the subject of extensive experimental and theoretical work during the last decades [1-5]. The fundamental magnetic, electronic and optical properties of these systems are quite different from their pure semiconductor counterpart, and over the last years, it has been shown that these properties are greatly influenced by the presence of charged carriers and the localized magnetic moments of the ions, leading to strong magnetotransport and magnetooptical effects. These phenomena have been widely studied and understood in Mn-based DMS in which the magnetic moments of the Mn ions interact antiferromagnetically [6]. More recently, a new generation of transition metal-based compounds such as ZnGeP2 [7], ZnGeSiN2 [8], and CuAlS2 [9], has been attracting attention because of several exciting new properties such as spin injection, carrier induced ferromagnetism, optically controlled magnetic order, eTC. These materials have opened a door into the field of new magnetic materials and ferromagnetic/semiconductor hybrid structures for applications in spintronics and spin-related devices [10,11]. The main features of these alloys are the presence of vacancies, interstitial atoms, and anti-site atoms, and it is expected that when diluted into the solid matrix, the magnetic ion interacts with these defects forming pairs with low configuration energy. Theoretically, the origin of ferromagnetic ordering in DMS could be connected to point defects responsible for the magnetic ion shelter and p-type carrier concentration induced by holes generation [12]. Experimentally, several techniques are available for studying the magnetic properties of DMS. Ferromagnetic Resonance (FMR) has proven to be one of the ideal techniques to study anisotropies and magnetic ordering in magnetic materials [13]. This is because the resonance spectrum is very sensitive to properties such as local anisotropies, magnetic interactions between intrinsic defects, and magnetic and structural inhomogeneities in the sample.
Ternary I-III-VI2 alloys are well known by their potential applications in the photovoltaic cells, light-emitting-diodes (LEDs), and in nonlinear optical devices [14]. The most studied are those of the family Cu-III-VI, which possess high absorption coefficient [15] and energy gap near to the optimum range for conversion of solar energy [16]. Although this, the capability of diluted magnetic semiconductors of the type I-III-VI2 as candidates for ferromagnetic/semiconductor hybrid structures is an unexplored issue. The aim of this work is addressed to test the ferromagnetic properties of the I-III-VI2 diluted magnetic semiconductor CuGa1- xMnxTe2, by means of Ferromagnetic Resonance (FMR). The paper is organized as follows. In the section II the experimental methods are briefly described. Section III is devoted to the theoretical model used to interpret the experimental data. In section IV, our results are discussed and analyzed. In section V the main results of this work are summarized.
Experimental
Samples of the I-III-VI2 diluted magnetic semiconductor CuGa1- xMnxTe2 with Mn composition x=0.05 to 0.25 were prepared by direct fusion of the stoichiometric mixture of the elements of at least 5N purity in graphite crucibles inside evacuated quartz ampoules (≈10-6Torr). To minimize the risk of explosion due to exothermic reaction between the group III element and Te, the ampoules were heated in a vertical furnace very slowly at 5K/h up to 1100 °C. Kept at this temperature for 24h, the samples were rocked at regular intervals to achieve a homogeneous mixing of the liquid phase of the reacting mixture, and then cooled to 500 °C at a rate of 5K/h. At this temperature the ampoules were annealed for 4 days. To test ferromagnetism in CuGa1-xMnxTe2 the ferromagnetic resonance spectrometry has been used. The ferromagnetic resonance field was measured as a function of temperature and Mn concentration, in an x-band VARIAN spectrometer, employing a homemade cylindrical cavity with Q factor of the order of 2000, adjusted in the TE100 mode. The magnetic field is supplied by an electromagnet mounted onto a 0-360 degrees base that allowed us to rotate the sample with respect to the direction of the applied field. With this, we were able to measure the angular symmetry of the FMR signal. The magnetic field was applied parallel to the plane of the sample. All spectra were taken at 9.35GHz cavity, and in the temperature range 90 K< T< 300 K. The temperature was calibrated using a carbon-glass thermometer.
Theoretical Background
The dynamics of the magnetization in a macroscopic ferromagnet is usually described using the Landau-Lifshitz-Gilbert equation (LLGE) of motion,
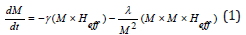
where M is the magnetization; Heff=-∇M E is the effective field, E is the magnetic free energy; λ is a relaxation frequency related to the viscous damping of the magnetization; and γ=1.4gMn (GHz/ KOe) is the gyromagnetic ratio for Mn. If our system is considered as a collection of magnetically oriented grains or particles, then the magnetic free-energy can be expressed as
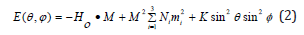
where the first term is the Zeeman energy at a magnetic field H0, Ni are the demagnetizing factors of the material, mi the director cosines of the magnetization M in spherical coordinates, the third term is the anisotropy energy with anisotropy constant K, and (θ, φ) are the spherical angles. At equilibrium, (θ =θ0,φ =ϕ0), the LLGE has the periodic solution M exp(iωt), where ω is the resonance frequency given by the condition [17].
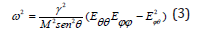
where θθ ϕ ϕθ E ,E ,E are the second derivatives of the free energy evaluated at the equilibrium positions. After performing the second derivatives of the free energy, the equation (3) is written as
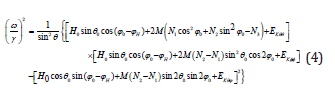
Here, EKƟƟ, EKϕϕ, EKƟϕ are the angular derivatives of the anisotropy energy evaluated at the equilibrium positions. Suppose now that our system consisted in arranged single domain uniaxial particles (grains) in the form of ellipsoids of rotation (N1=N2=N⊥; N3=N|| with saturation magnetization M=N0μ0/V0, being μ0 and V0, the particle moment and particle volume, respectively, and anisotropy energy given by EK= K sin2ƟƟ sin2ϕ. The field is applied in the xy-plane parallel to the plane of the sample (ƟH=π/2), with the magnetization along the uniaxial axis. At resonance, the magnetization follows approximately the external field so the equilibrium angles are Ɵ0≅ π/2, ϕ0≅ϕH so equation (4) is simplified to the form
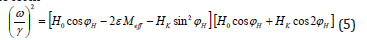
which gives the resonance field for any orientation, ϕH

where
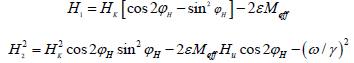
According to this, the resonance field is uniquely determined in the range from ϕ0=ϕH=0 (easy uniaxial axis) to ϕ0=ϕH=π/2 (hard uniaxial axis), such that HR (0)≤ HR(ϕH)≤ HR (π/2). In the case when the condition 4πMeff>>Hk is fulfilled, the FMR field is purely uniaxial and given by the simplified form
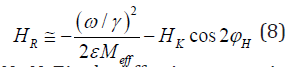
where Meff = N||-N⊥is the effective magnetization, Hk is the uniaxial field defined as 2K/M, and ε=±1 representing an ellipsoid with the shape of a spheroid (+) or an ovoid (-). Equation (8) is then compared to the experimental values of the resonance field to determine the three parameters Meff, Hk and g-factor.
Results and Analysis
The FMR spectra of the sample CuGa0.75Mn0.25Te2 are shown in
Figure 1, for several temperatures and for a fixed field orientation.
The FMR absorption is characterized by: (a) sharp low-field peak
below ∼235 K, and (b) weak high-field signal above 235K. No
signal was detected for temperatures < 90K. All signals showed
asymmetrical lines-shapes which reflect some electron properties
of these alloys. By rotating the plane of the sample with respect
to the field direction we have studied the anisotropic properties
of CuGaxMn1-xTe2. In Figure 2 we present the angular dependence
of the low-field peak recorded at T ~220 K, and for several Mn
concentrations. In the samsple with x=0.05 the resonance field
shows no clear evidence of any anisotropy; however, a uniaxial
symmetry is observed for Mn content x≥0.10. The solid curves in
Figure 3 are numerical fits of Equation (7) to the experimental data.
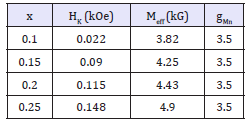
The corresponding parameters obtained from these fits are listed
in Table 1. Fairly good agreement between theory and experimental
data is obtained assuming ovoid particles (ε=-1) with gMn fixed at
3.5. This means that in average, there is an orbital contribution to
the total angular momentum of Mn. It is also observed from Table 1
that both, Hk and Meff, increase with Mn concentration. No angular
variation was observed for the high-field peak, and it is detected
in between the field range from 3440Oe to 3670Oe, depending
on the Mn concentration. The temperature behaviour of the lowand
high-field resonances is shown in Figure 3, for all values of
x. The measurements were taken at the position of maximum
resonance (ϕH≅π/2). The solid curve was calculated using the
resonance field given in Equation (8) with 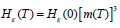 and
and 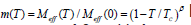 [18], being TC the Curie-Weiss
temperature, and β a critical exponent of the order of ≈0.40. For
Hk(0), M(0) and g, we have used the values 0.10kOe, 6.6kG and 3.5,
respectively. For the Curie-Weiss temperature we have used the
value TC=232K, which is very close to that reported in the literature
for these alloys, TC≅240K [19]. The dashed lines correspond to
the resonance condition for a paramagnet (HR=ω/γ) with g-factor
varying from 1.88 to 1.98, in the whole range of x. These findings
are in contrast with previous works suggesting a ferromagneticto-
superparamagnetic transition at TC, in CuGa1-xMnxTe2 [20,21].
The behavior of the g-factor is also of interest for DMS-based
spintronic devices in which relatively high effective g-factors are
required and could well bear more detailed experimental attention
in ferromagnetic semiconductors.
[18], being TC the Curie-Weiss
temperature, and β a critical exponent of the order of ≈0.40. For
Hk(0), M(0) and g, we have used the values 0.10kOe, 6.6kG and 3.5,
respectively. For the Curie-Weiss temperature we have used the
value TC=232K, which is very close to that reported in the literature
for these alloys, TC≅240K [19]. The dashed lines correspond to
the resonance condition for a paramagnet (HR=ω/γ) with g-factor
varying from 1.88 to 1.98, in the whole range of x. These findings
are in contrast with previous works suggesting a ferromagneticto-
superparamagnetic transition at TC, in CuGa1-xMnxTe2 [20,21].
The behavior of the g-factor is also of interest for DMS-based
spintronic devices in which relatively high effective g-factors are
required and could well bear more detailed experimental attention
in ferromagnetic semiconductors.
Figure 1:FMR spectra of the sample with x=0.25 for all temperatures. Observe the weak peak appearing at T≈235 K.
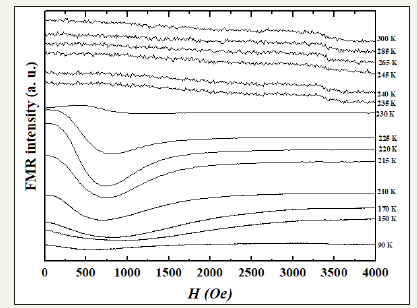
Figure 2:Angular dependence of the low-field resonance peak for: (a) x=0.10; (b) x=0.15; and (c) x=0.25. The measurements were performed at T~200 K.
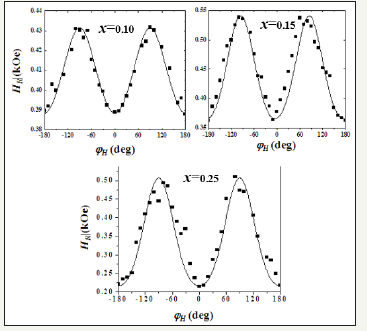
Figure 3:Temperature dependence of HR for all samples, taken with the magnetic field applied in the vicinity of maximum resonance (H=/2).
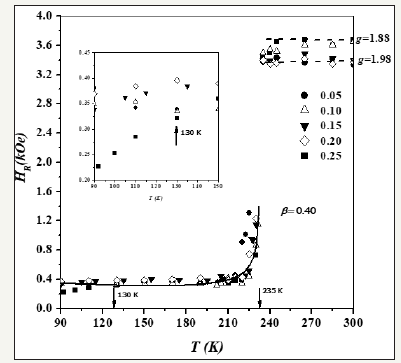
Table 1:Magnetic parameters of CuGa1-xMnxTe2 obtained from fitting the FMR field with Equation (7).
Also, of interest is the fact that in the sample with x=0.25 the
value of HR a small shift to lower fields is observed at temperatures
lower than ∼130K. Qualitatively similar behavior has been reported
in other Mn-based semiconductors which exhibit a ferromagnetic
phase at low temperatures [22]. It has been suggested that in these
materials, the ferromagnetism is mediated by holes and governed by
the RKKY mechanism [23,24]. In this scenario Mn2+ ions substitute
Ga3+ atoms to form the solid solution 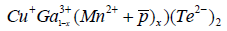 , with a p hole bounded to a Mn2+ ion at the Ga3+ site. At Mn
concentrations x< 0.20, the density of holes that contribute to the
effective magnetization of the Mn grains, is not sufficiently high to
induce a significant increase in the magnetization, so the resonance
field remains unchanged below the Curie-Weiss temperature.
However, above certain Mn concentration, the density of holes
increases so the magnetization of the FM grains is enhanced, and
a continuous decrease in the value of HR is then observed below
a critical temperature. This argument is supported by resistivity
measurements which show the behavior of the density of holes
with respect to temperature and Mn content in CuGa1-xMnxTe2 [20].
, with a p hole bounded to a Mn2+ ion at the Ga3+ site. At Mn
concentrations x< 0.20, the density of holes that contribute to the
effective magnetization of the Mn grains, is not sufficiently high to
induce a significant increase in the magnetization, so the resonance
field remains unchanged below the Curie-Weiss temperature.
However, above certain Mn concentration, the density of holes
increases so the magnetization of the FM grains is enhanced, and
a continuous decrease in the value of HR is then observed below
a critical temperature. This argument is supported by resistivity
measurements which show the behavior of the density of holes
with respect to temperature and Mn content in CuGa1-xMnxTe2 [20].
Conclusion
The diluted magnetic semiconductor CuGa1-xMnxTe2 was
synthesized and studied the ferromagnetic properties using
the FMR technique. The FM order in these materials is mainly
determined by the formation of ovoid uniaxial Mn grains with a
g-factor greater than 3.0. As the temperature approaches the Curie
point, the g-factor recovers the free electron value, indicative of an
ordered transition from the ferromagnetic state to the paramagnetic
state. This is explained assuming a particle effective magnetization
satisfying the law 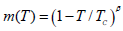 . In highly concentrated systems
the FMR field shifts gradually to lower fields as the temperature is
decreased below a critical value. Such a shift of the resonance field
could be related to a thermal increase of the effective magnetization
of the individual Mn grains. Several questions arise from this work:
(a) the origin of the transition at TC; (b) the effect of the main
grain size on the magnetic ordering; (c) the relation between the
anisotropy field and the Mn concentration; (d) the real dependence
of the particle magnetization with respect to temperature. Besides
this, the control of the main grain size opens the possibility for
manipulate the magnetic properties of Mn-doped ternary I-IIIVI
2 alloys, and to increase the scientific understanding of these
materials for possible use in spintronics applications.
. In highly concentrated systems
the FMR field shifts gradually to lower fields as the temperature is
decreased below a critical value. Such a shift of the resonance field
could be related to a thermal increase of the effective magnetization
of the individual Mn grains. Several questions arise from this work:
(a) the origin of the transition at TC; (b) the effect of the main
grain size on the magnetic ordering; (c) the relation between the
anisotropy field and the Mn concentration; (d) the real dependence
of the particle magnetization with respect to temperature. Besides
this, the control of the main grain size opens the possibility for
manipulate the magnetic properties of Mn-doped ternary I-IIIVI
2 alloys, and to increase the scientific understanding of these
materials for possible use in spintronics applications.
Acknowledgement
The authors wish to acknowledge the Venezuelan institution Condes-Luz, for partially supporting this work. We also thank Dr Pedro J Silva, from the Condensed Matter Lab, IVIC, Venezuela, for technical assistance in the FMR experiments.
References
- Furdyna J, Kossut J (1986) Diluted magnetic semiconductors, semiconductors and semimetals. Academic Press, Vol. 25, Boston, USA.
- Freeman J, Zhao YJ (2003) Advanced tetrahedrally-bonded magnetic semiconductors for spintronic applications. J Phys Chem Solids 64(9- 10): 1453-1459.
- Diwekar M, Borchers JA, Donovan KVO, Halperin J, Awschalom DD, et al. (2004) Magnetic properties of (Ga,Mn) as digital ferromagnetic heterostructures. J Appl Phys 95(11): 6509
- Gavriljuk VG, Dobrinsky A, Shanina BD, Kolesnik SP (2006) A study of the magnetic resonance in a single-crystal Ni(50.47) Mn(28.17) Ga(21.36) alloy. J Phys Condens Matter 18(32): 7613-7627.
- Zutic, Fabian J, Das Sarma S (2006) Spintronics: Fundamentals and applications. Rev Mod Phys 76: 165-203.
- McCarty D, Hassan AK, Brunel LC, Dziatkowski K, Furdyna JK (2005) Electron paramagnetic resonance shift in II1−xMnxVI diluted magnetic semiconductors in the presence of strong exchange coupling. Phys Rev Lett 95: 157201-1.
- Cho S (2002) Phys Rev B 65: 257203.
- Pearton SJ, Abernathy CR, Overberg ME, Thaler GT, Norton DP (2003) Wide band gap ferromagnetic semiconductors and oxides Journal of Applied Physics 93(1): 10.1063-1.1517164.
- Chu, Osinsky A, Fuflyigin V, Zhu LD, Polyakov AY, et al. (2002) Magnetic and structural characterization of Mn-implanted, single-crystal ZnGeSiN2. J Appl Phys 92: 2047.
- Freeman YJ, Magn J (2002) First-principles prediction of a new class of ferromagnetic semiconductors. Magn Mater 246(1-2): 145.
- Ohno H (1998) Making nonmagnetic semiconductors ferromagnetic. Science 281(5379): 951-955.
- Redinski P, Rappoport TG, Libal A, Furdyna JK, Jankó B, et al. (2005) Optical response of a ferromagnetic-diluted magnetic semiconductor hybrid structure. Appl Phys Lett 86: 113103.
- Zhao YJ, Alex Z (2004) Electronic structure and ferromagnetism of Mnsubstituted CuAlS2, CuGaS2, CuInS2, CuGaSe2 and CuGaTe2 Phys Rev B 69(10): 104422
- Michael Farle (1998) Ferromagnetic resonance of ultrathin metallic layers. Rep Prog Phys 61(7): 755.
- Rockett RW, Birkmire J (1991) CuInSe2 for photovoltaic applications. Appl Phys 70(7): 10.1063-1.349175.
- Hovel HJ (1975) Semiconductors and semimetals. In: Willardson K, Beer AC (Eds.), Solar Cells, Acad Press, NY, USA, 2: 71-92.
- Chopra L, Tiwari AN (1987) Ternary and multinary compounds. In: Deb SK, Zunger A (Eds.), Materials Research Society, USA, p. 49.
- Suhl H (1955) Ferromagnetic resonance in nickel ferrite between one and two kilomegacycles. Phys Rev 95(2): 555.
- Callen HB, Callen E (1966) The present status of the temperature dependence of magnetocrystalline anisotropy, and the 1(1+1)2 power law. J Phys Chem Solids 27(8): 1271-1285.
- Lee WL, Pray T, Regan KA, Cava RJ, Bhatt RN, et al. (2002) APS March Meeting U16.4, Indianapolis, USA.
- Novotortsev VM, Shabunina GG, Koroleva LI, Aminov TG, Demin RV, et al. (2007) Superparamagnetism in Mn-doped CuGaTe2. Inorganic Materials 43(1): 12-17.
- Pérez, Silva PJ, Rincón CA, Ferrer JP, Fermin JR (2008) EPR study of the diluted magnetic semiconductor CuGa1-xMnxTe2. J Magn Magn Mater 320(17): 2155-2158.
- Story T, Eggenkamp PJT, Swuste CHW, Swagten HJM, Szczerbakow A, et al. (1993) Magnetic-resonance study of the diluted magnetic semiconductor Pb1−x−ySnyMnxTe. Phys Rev B 47(1): 227.
- Dietl T, Ohno H, Matsukura F, Cibert J, Ferrand D (2000) Zener model description of ferromagnetism in zinc-blende magnetic semiconductors. Science 287(5455): 1019-1022.
© 2018 José RF. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






