Electrical Charge Distribution on Carbon Surfaces as a Function of the pH and Point of Zero Charge. An Approximate Solution

Carbons are amphoteric by nature, which means that acidic and basic functionalities coexist on their surface. When a carbon is placed in an aqueous medium, these functionalities, depending on the pH and the nature of the functionalities, may give rise to positive or negative charges. Figure 1 summarizes the main proposed models for oxygen-containing functionalities, which are the most abundant surface groups present on carbons. Knowledge of how a carbon surface is charged is of crucial importance for a number of processes, particularly when carbon materials are used as electrodes.

Figure 1:Main proposed models of oxygen-containing surface groups that can be present on carbon surfaces and their evolution in acidic or basic media.

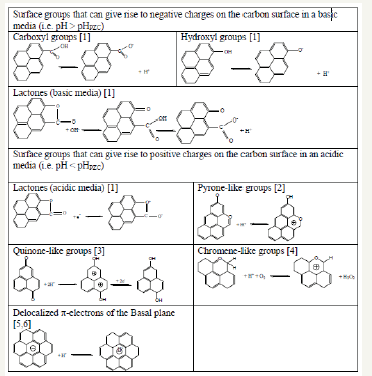
However, the charge developed by a carbon when it is put into contact with an aqueous solution cannot be accurately predicted given the complexity of the functionalities that typically coexist on its surface.

An approximate solution to this problem is provided by the following simple model (Figure 2): When the pH of an aqueous medium, and therefore the [H+], is altered by the addition of H+ (by adding, for example, an acid) or by the removal of H+ (by adding, for example, a base) the carbon surface trends to counterbalance the newly created situation by adsorbing H+ (or alternatively releasing OH− or e-) or by releasing H+ (or alternatively adsorbing OH− or capturing e−) respectively. This response mechanism gives rise to the formation of (new) positive or negative charges respectively on the carbon surface. Note that although equations given in Figure 1 are presented as equilibrium, this is merely a model, since carbons are in suspension (not in solution) and so, the classical equilibrium equations cannot be applied here.

Figure 2:Simplified representation of the charge exchange between the carbon surface and the aqueous media.

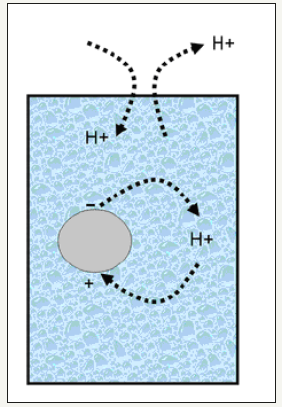
Assuming this simplification to be correct, the proportion of positive and negative charges on a carbon surface can be expressed as a function of the point of zero charge (pHpzc) (i.e., the nature of the carbon surface groups) and the pH (i.e., the nature of the aqueous medium).

The proportion of positive charges on a given surface can be then expressed as

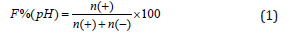
where n(+) is the number of positive charges and n(−) is the number of negative charges.

Assuming that the amount of positive charges is proportional to the concentration of protons in the aqueous medium and the amount of negative charges is inversely proportional to the concentration of protons (in accordance with the simplification made above) then [1-6]:

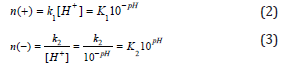
Substituting into equation (1), we obtain:

Multiplying by10pH:

Dividing by k₁ and defining k as k₁/k₂

Taking into account the definition of the point of zero charge:

given that at the point of zero charge (pHpzc) the amount of positive charges must be equal to the amount of negative charges, then:

Substituting k into equation (6):

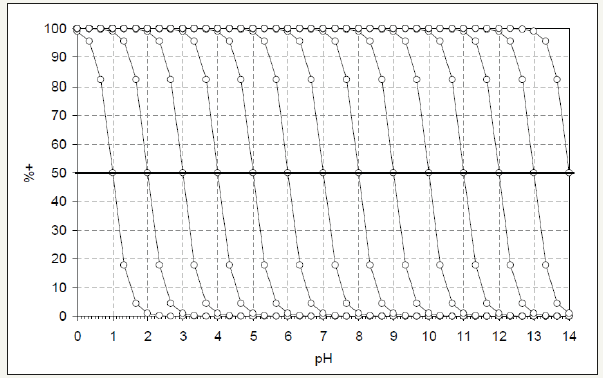
This function can be represented for different pHpzc in the following diagrammatic form (Figure 3).

Figure 3:Percentage of positive charges on a carbon surface as a function of the pH of the medium. Each curve represents a different carbon, whose pHpzc is the pH at which the curve intersects the 50% charge line.

Assuming the above line of reasoning to be valid, then only when pH = pHPZC, are the carbon surfaces neutral. A slight shift in this situation (ca. 1 unit of pH) would give rise to a carbon surface that is either totally positively or negatively charged. This means that, in practice, carbon surfaces will be negatively charged when the pH of the aqueous medium is slightly above the pHPZC or vice versa.

This model allows the relative proportion of electrical charges to be known, but not their amount. However, it seems reasonable to suppose that the greater the difference between the pHPZC and the pH of the aqueous medium, the greater the amount of electrical charges (either positive or negative, depending on the situation).

In any case, this may serve as a starting point for making more sophisticated calculations in order to ascertain the electrical charge distribution on carbon surfaces.

1. León CA, Radovic LR (1994) Chemistry and physics of carbon. In: Dekker, New York, USA, 24: 151.
2. Suárez D, Menéndez JA, Fuente E, Montes-Morán MA (1999) Contribution of pyrone-type structures to carbon basicity: An ab-initio study. Langmuir 15: 3897-3904.
3. Moran MA, Suárez D, Menéndez JA, Fuente E (2012) The basicity of carbons. In: Tascon JMD (Ed.), Novel Carbon Adsorbents, Elsevier, Netherlands, pp.173-203.
4. Garten VA, Weiss DE (1957) A new interpretation of the acidic and basic structures of activated carbon in relation to its behavior as a catalyst and adsorbent. II. The chromene-carbonium ion couple in carbon. Aust J Chem 10: 309-328.
5. León CA, Solar JM, Calemma V, Radovic LR (1992) Evidence for the protonation of basal plane sites on carbon. Carbon 30: 797-811.
6. Morán MA, Menéndez JA, Fuente E, Suárez D (998) Contribution of the basal planes to carbon basicity: An ab-initio study of the H2O+- π interactions in cluster models. J Phys Chem B 102: 5995-5601.