Electron and Neutron Degeneracy on Stellar Life Cycle

Ancient civilization pinpointed stars thousands of years ago. Stars have been found as a symbol of love, fear, and worship in different ancient civilization. Around the 15th century, Giordana Bruno proposed the similarity between the sun and the stars [1]. Our understanding of the science of the stars has been influenced by many physicists especially Isaac Newton and Albert Einstein. The first measurements of a distance to stars than sun have been made in the 19th century [1]. Within a couple of centuries, to be exact from 1850 to present, astronomers detected four billion stars in our own Galaxy Milky Way [2,3]. While our understanding of the stars is ever increasing, lack of knowledge of the fundamental particles and quantum gravity poses a problem to speed up our understanding of more recent discoveries as dark energy and dark matter. Simple nature of statistical laws has been proven effective to explain the man-made semiconductors to nature’s exotic objects like stars and a black hole. The mystery of stars is dated back to the early human civilization while thermodynamics and statistical mechanics was much younger science [4,5]. Often, the extreme end of any physical laws is present in the astronomical objects [6,7]. To the surprise of many, statistical mechanics along with few other physical laws can explain the formation, evaluation, and death of astronomical objects in reasonable detail. In this paper, different phases of a star’s life have been discussed with the help of statistical mechanics, thermodynamics, and quantum mechanics.

Stellar evolution

Star is a massive object with a large mass. Stars mass usually varies from 0.01 solar mass (Ms) to 50Ms [8]. It is usually composed of 91% H, 9.9% He, and 0.1% other materials. [9] Star radius varies the most over many orders of magnitude from few kilometers to few billion km. Stars can be classified by different parameters like sizes, spectra, density, distance, orbital path, and temperature. For our discussion, classification of stars in terms of the mass, size, and density is of importance. Many times, mass alone determines the entire lifecycle of a star. Stars are born from the cosmic dust and grow due to gravity. After the initial formation period, a star stabilizes with a certain mass and temperature. Most of the stars in the night sky have an active core and called the main sequence stars. After the active phase, a star turns into red giants. During this phase, star loses its outer layer and around half of its primary mass [10]. Depending on the initial mass, a star may become a white dwarf, neutron star or a black hole. In our discussion, we will talk about all the stages except the red giant phase since it is too complicated for this paper.

Gravity attracts stellar dust and shrinks the star. Gravitational potential energy goes down as a result. As star shrinks, the gravitation potential energy decreases but kinetic energy increases. Temperature increases with kinetic energy. Protons fuse in a thermonuclear reaction and produce an outward pressure. So, the pressure due to the burning fuel opposes the gravity. Birth of stars can simply be explained via the help of the Virial’s theorem which can be described as “for a bound gravitational system, the longterm average of its kinetic energy is one half that of its potential energy” [11]. This theorem can be expressed as follow.

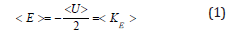
Where < E> is the long-term average of the kinetic energy of a star and < U> is the potential energy. This theorem is equally applicable for any energy arising from a force having inverse square distance dependence (Bohr atom/gravity). Stellar dust initially separated by a larger distance come together to form the star due to the gravitational force. During the formation, potential energy of the particles decreases. From the conservation of the energy, we know some other form of energy must increase. Virial’s theorem proves that the decrease of the potential energy should be compensated by the increase in kinetic and radiative energy [12].

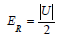
Let us assume the star been formed by the gradual addition of the spherical layer of dr and mass dm. Assuming the linear profile of the density of the star, the calulation is provided below.

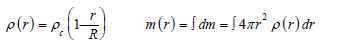
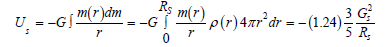
Figure 1:Nonlinear density and potential energy profile of the star.

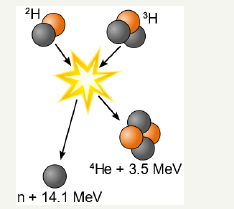
Figure 2:Energy release during a proton-proton cycle.

High mass concentration in the core causes the star density to be nonlinear. The potential energy of the atoms for a nonlinear density has been plotted in Figure 1 & 2. The radiated energy per unit area per unit time is related to the temperature through the Stephan’s Boltzmann law.

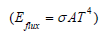
Among many, one of the big differences between a star and a planet is the difference between their radiated energy. The gravitational collapse during the formation of the star causes the total energy to decreases (half energy radiated away) [13]. One would assume the temperature should decrease too as a result. But the increase in kinetic energy increases the internal energy/ temperature.

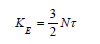
Since the gravity is strongest in the center of a star, the temperature is also high in the center. The radiation pressure coming from the star is not sufficient to provide the observable luminosity. This indicates the presence of some other form of energy inside the stars. When the stars temperature in the core increases, thermonuclear fusion between the hydrogen atoms produces Helium and releases a huge amount of heat. Calculated core temperature of the star classically forbids the fusion reaction at the temperature on the order of Million Kelvin. Calculated at the temperature 107K, Maxwell Boltzmann distribution provides the probability of the fusion reaction on the order of 10-423 (Equation 2). However, the positively charged proton overcomes the Coulomb barrier via quantum mechanical tunneling (Equation 3).

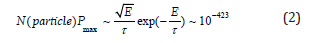
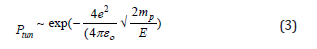
After the star exhausts all the hydrogen, further fusion to more massive element depends on the temperature of the core and thus the potential energy of the core. The more massive the star, higher the potential energy as well as the temperature in the core. A star a few times heavier than the sun can fuse element up to carbon, oxygen, and so on. A more massive star can fuse all the way to Fe atom. Fe fusion is endothermic. Fe absorbs heat and thus the core temperature decreases. At this point, the fusion reaction is no more thermodynamically favorable. Some exotic events like supernovae can provide enough energy to fuse heavier element.

White dwarf

Main sequence stars having an initial mass less than eight solar masses converts to White Dwarf at the end of their active phase. Once the star exhausts all the hydrogen in core temperature is not high enough to fuse Helium/Carbon and so on. This shifts the core from hydrostatic equilibrium and gravity stars pulling the mass towards the core again resulting in lowering potential energy. This causes the kinetic energy and thus temperature to increase in the core. Now we have electrons in the core having high energy and density. But the Fermi energy of the electrons goes up at the density of the electrons increases. This phenomenon can be explained by the help of Pauli exclusion and Heisenberg uncertainty principle. Exclusion principle says the electron cannot be close enough to have the same wave function. Once the electrons are constrained by space, Uncertainty principle states momentum should be at least as high as the magnitude of the uncertainty of the momentum. At this phase, stars can be approximating as metals and it has a sea of electrons confined in high concentration. Following the Fermi energy concept in the metals, the kinetic energy calculations of the stars electron are given below [14,15]

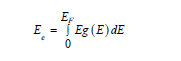
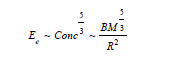
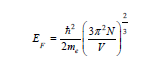
Figure 3:Normalized variation of electronic and Fermi energy of the electron.

Variation of the fermi energy and the total electronic energy of a typical white dwarf result from a sun-like star have been illustrated in the Figure 3. Electronic and fermi energy have been normalized with respect to their maximum energy of 1.07MeV and 6*1044J. Nonlinear variation of the energy with increasing concentration stops further contraction of the WD radii in the degenerate electron gas. The more accurate calculation at this high energy requires a relativistic expression for electron energy which is discussed in the next section for Neutron stars in detail.

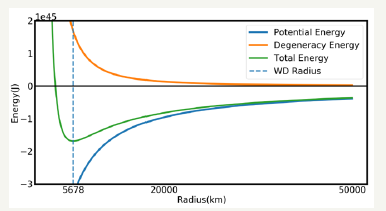
Kinetic energy (Ee) of the electrons have 1/R2 dependence in the non-relativistic scenario like White Dwarf. Previously, we have seen that the potential energy decreases as 1/R. So, there should be an optimum radius where the total energy minimizes. The equilibrium radius due to the degenerate electron pressure [16] is plotted in Figure 4. It also shows the variation in the kinetic, potential, and total energy with radius. White dwarf radiates very slowly due to the dead core and sustains in this phase for trillion years till they become a black dwarf. Currently, the universe is not old enough for the presence of a Black Dwarf.

Figure 4:Total energy and equilibrium radius of the White Dwarf.

A recent article in nature [17] reports a high concentration of O2 found in a white dwarf core than the predicted value from the current stellar models. Since 97% of all the stars will end up being a white dwarf in the universe, this leads us to rethink our current understanding of the stellar events and requires further research in this field. Unlike recently, most of the white dwarf is thought to be non-magnetic to cause accretion. A white dwarf with a magnetic impulse followed by no radiation is reported in binary systems [18]. Released burst increases the potential energy of the highly compressed core of the remnant star. A burst of this kind is highly directional like synchrotron radiation in a particle accelerator and shows light house like effect [19]. Unlike pulsar, white dwarf accretion is found only in tight orbit usually in a binary system due to lesser mass.

Neutron stars

If the main sequence star is between 8 to 25 solar masses, electron degeneracy pressure is not strong enough to compensate the massive gravitational pure of the dense core of the star. Shrinking in the radius causes the concentration to go far above the quantum concentration and kinetic energy skyrockets. In this energy range, electrons can no longer be treated as a classical particle. The relativistic energy of the electrons almost as much as the total energy of the electrons. The classical kinetic energy of an electron in a potential well is no longer valid now. The density of states and Fermi energy equations depends on the validity of the classical parabolic energy-momentum dispersion. So, they are no longer valid too. The density of the states can still be calculated in the momentum space in terms of Fermi momentum. The density of the states is used to find the total number of states, so defining it in terms of the momentum poses no problem in calculating total energy.

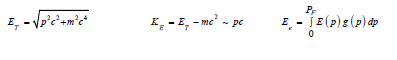
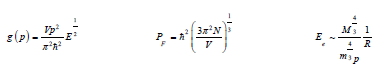
Figure 5:Total energy curve below and above the Chandrashekar mass of a star.

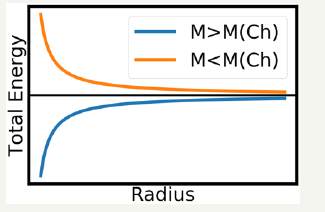
Relativistic electron energy calculations above show the electron energy (Ee) in the relativistic case vary as 1/R unlike the classical dependence as 1/R2. Now both the kinetic and potential energy varies as 1/R and there is no minimum in the total energy curve (Figure 5). b It can be shown that the total energy curves differ depending on the mass of the star relative to Chandrasekhar Mass( MCH=1.44 MS). The total energy curve has been depicted in Figure 4. When the mass is lower than MCH, total energy minimizes as radius decrease. This causes the decrease in kinetic energy and temperature which further results of the electrons behaving classically. Classical electrons no longer follow the relativistic equations and ends up as White Dwarf star. When the mass is greater than the MCH, total energy decreases when the radii decrease. Relativistic electron now has high enough energy to overcome the reaction enthalpy with the protons. So, now the electrons combine with proton and turn into neutrons and neutrino (ve) which can be expressed as follow.

Neutrino does not react much with the matter and escapes the star. Now the star has a neutron core. Some ions, electrons in the outer shell, and iron and heavy elements on the surface. The star will continue to collapse if there is nothing else to prevent it. But the neutrons are fermions too and the degenerate fermions radiation pressure stabilizes the star in a radius inversely proportion to the 1/3 power of the mass, which has been expressed by the following expression [20].

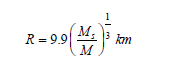
The gravitational constant of the neutron star is 11 orders of magnitude higher than the earth, which can be expressed as follow [21].

So far it is the densest observable astronomical object in the universe. Conservation of the angular momentum causes the neutron stars to rotate very fast [22]. Surface iron and ions make neutron star behave as a magnetic dipole and radiate along the magnetic axis. Such a neutron star is called a Pulsar. Power of the magnetic dipole radiation of the Pulsars can be attributed to the loss of the gigantic rotational energy.

Black Hole

When the main sequence star is massive than the 25 solar masses, neutron radiation pressure is not strong enough to hold the collapse against the massive gravitational pull. Thermodynamics and gravity at this range are better to describe by general relativity and quantum mechanics and quite out of scope from the discussion of this paper. All the masses of the black holes are assumed to be present at a single point and thus it turns the space-time into a singularity. A black hole is one of the most exotic objects of entire science and requires further investigation to improve our understanding of them.

Current struggle of science is to find the fundamental forces and particle’s behaviors at extreme conditions. Stars give us an opportunity to test our understanding of such a scale. Stars also give us an evaluation characteristic over a grand timescale otherwise not achievable by humans. Future growth in science should focus on solving the many current mysteries of the universe with laws as simple as uncertainty principle.

The authors would like to acknowledge Kartik Ghosh and Jingtian Fang for their useful feedbacks.

Both Mahmud Reaz and Ariful Haque designed the study, interpreted the idea of the article, conducted analysis on the topic, and designed and wrote the manuscript. Mahmud Reaz contributed to manuscript formation and development of the work. Ariful Haque assisted in evaluating and editing the manuscript. All authors gave final approval and agreed to be accountable for all aspects of the work.

1. Cain F (2009) History of stars - universe today.
2. Krauss LM, Chaboyer B (2003) Age estimates of globular clusters in the milky way: constraints on cosmology. Science 299(5603): 65-69.
3. Pinto JHR, Scalo J, Maciel WJ, Flynn C (2000) An intermittent star formation history in a ‘normal’ disk galaxy: the milky way. Astrophys J 531(2): L115–L118.
4. Israel W (1981) Thermodynamics of relativistic systems. Phys A Stat Mech its Appl 106(1-2): 204-214.
5. Chavanis PH (2002) Statistical mechanics of violent relaxation in stellar systems. Multiscale Problems in Science and Technology, Berlin, Heidelberg: Springer Berlin Heidelberg, Germany, pp. 85-116.
6. Adams FC, Lada CJ, Shu FU (1987) Spectral evolution of young stellar objects. Astrophys J 312: 788.
7. Caditz D, Petrosia V (1990) Statistical and physical evolution of quasistellar objects. Astrophys J 357: 326.
8. Nieuwenhuijzen H, De Jage C (1990) Parametrization of stellar rates of mass loss as functions of the fundamental stellar parameters M, L, and R. Astron Astrophys 231: 134-136.
9. Wallerstein G, Iben I, Parker P, Boesgaard AM, Hale GM, et al. (1997) Synthesis of the elements in stars: forty years of progress. Rev Mod Phys 69(4): 995-1084.
10. Fowler A (1889) Stellar Evolution. Nat 1889: 401026.
11. Miller GE, Scalo JM (1978) On the birthplaces of stars. Publ Astron Soc Pacific 90(537): 506.
12. Kippenhahn R, Weigert A (1990) The virial theorem, pp. 15-18.
13. Kippenhahn R, Weigert A (1990) Conservation of Energy, pp. 19-26.
14. Anderson PW (1961) Localized magnetic states in metals. Phys Rev 124(1): 41.
15. Quinn JJ (1962) Range of excited electrons in metals. Phys Rev 126(4): 1453-1457.
16. Kippenhahn R, Weigert A (1990) The degenerate electron gas, pp. 118- 128.
17. Giammichele N, Charpinet S, Fontaine G, Brassard P, Green EM, et al. (2018) A large oxygen-dominated core from the seismic cartography of a pulsating white dwarf. Nature 554(7690): 73-76.
18. Scaringi S, Maccarone TJ, Angelo CD, Knigge C, Groot PJ (2017) Magnetically gated accretion in an accreting ‘non-magnetic’ white dwarf. Nature 552(7684): 210-213.
19. Buckley DAH, Meintjes PJ, Potter SB, Marsh TR, Gänsicke BT (2017) Polarimetric evidence of a white dwarf pulsar in the binary system AR Scorpii. Nat Astron 1(2): 29.
20. Chandrasekhar S (1994) The maximum mass of ideal white dwarfs. J Astrophys Astron 15(2): 115-116.
21. Thorsett SE (1996) The gravitational constant, the chandrasekhar limit, and neutron star masses. Phys Rev Lett 77(8): 1432-1435.
22. Gold T (1969) Rotating neutron stars and the nature of pulsars. Nature 221(5175): 25-27.