An Optimized Proposed Job Scheduling Technique

The term scheduler can also be described as a hardware that performs scheduling task. Advantages associated with schedulers are: it helps in keeping all the resources of computer unit busy. It also helps in creation of multi-user environment so that more than one user shares the resources of system simultaneously [1]. It also helps in maintaining the high QoS of the system. Scheduling uses the concept of calculation for allocation of task, and also it is a software part in the computer system that helps in increasing the efficiency of computer. The idea behind scheduling is to do multiple works simultaneously and by using only one processing unit. In order to schedule the jobs in several scheduling algorithms have used. Job scheduling algorithms are used to select a particular job for execution from a long queue. The basic job selection technique is based on dispatching rules. FCFS stands for first come first serve and it schedules the process on the basis of order in which jobs are assigned [2]. SPTF stands for Shortest Processing Time First and it is also known as Short-Job-First that is abbreviated as SJF, this algorithm used to allocate the job on the basis of job priority. Largest job first abbreviated as LJF, it allocates the highest priority to the process that need large time for execution. EDF stands for Earliest Deadline First used to allocate the highest priority to that job which have fixed deadline for execution. These techniques are simulated under the results section along with the proposed technique. In the existing techniques, distribution criterion or combination of different techniques was used to obtain minimum response time in completion of the jobs but this method does not perform well in varying load. So the concept of optimization has introduced in this work where the optimum solution is find out or continues the process until the maximum fitness value is not achieved. Thus, proposed technique is compared with the traditional technique to ensure the performance of individual technique. The major focus of job scheduling is to choose the optimum processors in a grid to allocate different jobs. In case of each processor, the creation of job schedulers is totally dependent on management system [3]. In grid scheduling the optimum calculation and process scheduling is major challenge.

From the literature it is studied that many researchers have introduced many algorithms for the job scheduling process. The job allocation depends on many factors as need of those systems are to finish the jobs on or before deadline the systems need to have consider all quality parameters. As the major need are to

a. Finish jobs on time

b. Over all waiting time should be less

c. Over all turnaround time (Finish Time) should be less.

By taking these terms under consideration the algorithm name FCFS, SJF, Round robin etc many algorithm had been developed. But still as the number of requirements and the jobs are increasing daily researchers put their efforts to develop new algorithms. In the reference paper the work is done on combining the two algorithms to prepare the hybrid model of scheduling. But those algorithm are valid upto an extent, as the requirements are to updated at some intervals then these algorithm might be unable to schedule the process efficiently. So there is need to find such a solution which can randomly provide solution with much efficient requirement handling approach.

In this section of paper, the results are acquired after performing traditional and the proposed technique and the obtained results are shown below in terms of mean response time. For the simulation purpose, different average arrival rate i.e. 24, 26 and 28. The traditional techniques which are used to perform comparisons are First Come First Serve, Shortest Job First, 50% of jobs were executed through FCFS and 50% are from Shortest Job first, 75% of FCFS and 25% of SJF, 10% through FCFS and 10% through SJF with the proposed technique i.e. GA-ST. the experimental analysis have performed and results acquired from this simulation is presented below [4-17].

The Figure 1 shows the comparison between different techniques with respect to mean arrival time 24. The comparison has done using FCFS with SJF technique with the proposed GA-ST technique with respect to mean response time. Table 1 comprised of values that are obtained from the graph and it depicts that the Mean Response Time of FCFS75-SJFS25 and FCFS10-SJFS10 is notified which is the highest time among all of other algorithms. Whereas the Mean Response Time of the GA-ST is the least as compare to others i.e. 2.3. The values represented in Table 1 are observed by considering the λ=24.

Figure 1: Comparison between traditional (FCFS-SJF) and proposed with 24 mean arrival time.

Table 1: Parametric values of Figure 1.

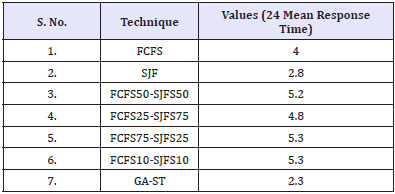
Firstly, jobs are accomplished using FCFS technique, then SJF technique has applied over the jobs and then distribution of different techniques according to the number of processes is applied. From the results, it concludes that FCFS complete its task with the response time at 4 whereas the distribution of different techniques such as FCFS50-SJF50, FCFS75-SJF25 and FCFS10-SJF10 positioned with highest response time 5 which is not appropriate for the system ‘s efficiency. Alternatively, proposed GA-ST takes least time i.e. consequently with the load i.e. 24 proposed techniques outperforms.

The Figure 2 shows the comparison between different traditional techniques with proposed technique. The experimental analysis is performed using the load 26 with respect to response time. From the Figure 2 it ensures that proposed technique performs effectively in comparison with other traditional techniques. The FCFS technique works not accordingly as the load increases so its performance degrades. Similarly, the other proportional techniques perform in inefficient manner with maximum response time.

But consider the shortest job first technique which performs better as compared to other techniques. On the whole, proposed GA-ST technique stands out in terms of rapidly competition of job in the system with 2.5 approx.

Table 2 comprised of values that are obtained from the graph of Figure 2 and it depicts that the mean response time of FCFS75- SJFS25 and FCFS10-SJFS10 is notified to 5.3 which is the highest time among all of other algorithms. Whereas the Mean Response Time of the GA-ST is the least as compare to others i.e. 2.67. The values represented in Table 2 are observed by considering the λ=26.

Figure 2: Comparison between traditional (FCFS-SJF) and proposed with 26 mean arrival time.

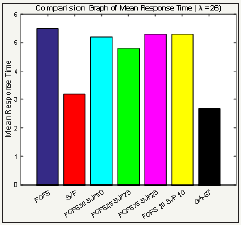
Table 2: Parametric values of Figure 2.

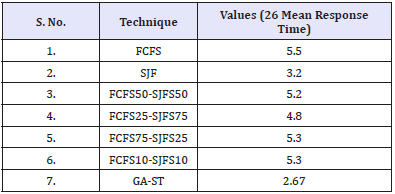
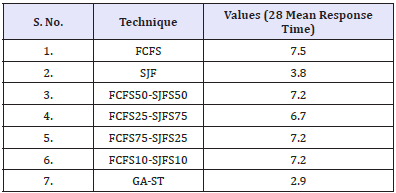
Figure 3 depicts the results acquired from the traditional techniques and proposed technique. Among all the techniques, proposed technique surpasses the other traditional techniques. FCFS does not perform effectively with the increase amount of load in the system. All the processes reach at 28 in the system. The technique with the less response time is considered as the most accurate technique and from the Figure 3 it can be clearly seen that combination of GA-ST performs best and respond within less time i.e. 2.5 approx despite the load in the system.

Initially, the shortest job collaborated with first come first serve technique was evaluated to consider their performance. Now FCFS with Shortest job first technique performance is evaluated with varying arrival time i.e. 24, 26 and 28.

Table 3 comprised of values that are obtained from the graph of Figure 3 and it depicts that the Mean Response Time of FCFS75- SJFS25 and FCFS10-SJFS10 is notified to 7.2 which is the highest time among all of other algorithms. Whereas the Mean Response Time of the GA-ST is the least as compare to others i.e. 2.9. The values represented in Table 3 are observed by considering the λ=28.

Figure 3: Comparison between traditional (FCFS-SJF) and proposed with 28 mean arrival time.

Table 3: Parametric values of Figure 3.

The Figure 4 shows the performance of FCFS, LJF, FCFS50- LJF50, FCFS75-LJF 25, FCFS10-LJF10 and proposed GA-ST. From the graph it has shown that among all the techniques, FCFS evaluates results and responds in less time i.e. 4 but other techniques with distribution performs does not appropriately and wrap up its job with highest time taken. Alternatively, GA-ST performed better with less response time i.e. 2.

Table 4 represents the values that are obtained from the graph of Figure 4 corresponding to FCFS, LJF, GA-ST and various combinations FCFS and LJF. It is observed that the GA-ST has least response time i.e. 2.3 and FCFS25-FFCFS75 is 6.5 which are highest as compare to others. The results are obtained by considering the λ=24.

Figure 4: Comparison between traditional (FCFS-LJF) and proposed with 24 mean arrival time.

Table 4: Parametric values of Figure 4.

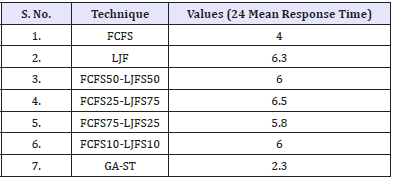
Figure 5: Comparison between traditional (FCFS-LJF) and proposed with 26 mean arrival time.

The Figure 5 exemplifies the results carried out with 26 mean arrival time. Hence, the results are acquired and shown in the below Figure 5. It concludes that every technique except LJF completes their task within less response time i.e. below 6 so distributions of processes within FCFS and LJF produces remarkable results but proposed GA-ST perform outstandingly with response time at 2.

Table 5: Parametric values of Figure 5.

Table 5 represents the values that are obtained from the graph of Figure 5 corresponding to FCFS, LJF, GA-ST and various combinations FCFS and LJF. It is observed that the GA-ST has least response time i.e. 2.67 and LJF is 11.5 which are highest as compare to others. The results are obtained by considering the λ=26.

The Figure 6 evaluates their performance with the load of 28. From the results acquired it ensures that proposed technique surpasses all the traditional techniques with least response time in responding and completion of task.

Table 6 represents the values that are obtained from the graph of Figure 6 corresponding to FCFS, LJF, GA-ST and various combinations FCFS and LJF. It is observed that the GA-ST has least response time i.e. 2.9 and FCFS25-LJFS75 is 9.8 which are highest as compare to others. The results are obtained by considering the λ=28.

Figure 6: Comparison between traditional (FCFS-LJF) and proposed with 28 mean arrival time.

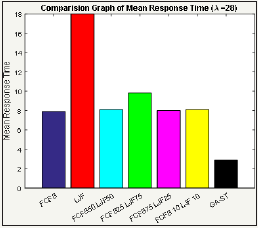
Table 6: Parametric values of Figure 6.

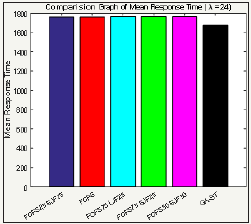
The Figure 7 portrays the performance of traditional techniques and proposed technique with mean arrival time 24. From the results acquired, the GA-ST performs better and responds in less time in comparison with other techniques where all of them stable at 1700 approx response time which means that the existing techniques are not efficient for the system.

Table 7 depicts the values on the basis of comparison that is shown in Figure 7. It draws a contrast among FCFS25-SJF75, FCFS, FCFS75-LJF25, FCFS75-SJF25, FCFS10-SJF10 and GA-ST with the value of λ=24. It is observed that the GA-ST poses the minimum Response Time as compare to other techniques.

Table 7: Parametric values of Figure 7.

Figure 7: Comparison between traditional and proposed techniques with 24 mean arrival time.

This work studies the performance of different traditional techniques which uses the policies of equal distributions among three job scheduling algorithms such as First Come First Serve, Shortest Job First and Largest Job First. These algorithms are combined together with one another using equal or unequal distribution. For the comparison purpose, these algorithms are compared with the proposed GA-ST algorithm. Comparing two job policies such as FCFS-SJF and FCFS-LJF, it has found that SJF performs better than LJF as the mean repose time with LJF varying from 6 to 8 which is quite higher and inappropriate for the system. Another factor which is considered in this work is with the increase in load the variability in service demand times is also increasing. Among all the traditional techniques SJF surpasses the other methods. Alternatively, the traditional methods have compared with the proposed GA-ST technique and it concludes that proposed technique outperforms the SJF also yielding the lower mean job response time as it was expected. Though, SJF performs better but proposed method performs well at high service demand variability. As the proposed technique has the capability to find best random solution for solving given problem so it works effectively with existing algorithms of job scheduling. Moreover, it is considered as the fairest as it performs on both short jobs as well as large jobs in queues. Additionally, there is slightly increment in average response time with respect to increase in workload λ. On the whole, LJF scheduling algorithm performs worst not only alone but with combined FCFS as well.

The proposed method can be extended with recent optimization algorithms with minimum response time. Moreover, the jobs which have hard deadlines can be considered in future to produce most efficient results.

1. Bhoyar AA (2015) Design and implementation of job scheduling in grid environment over IPv6. International Journal of Computer Science and Mobile Computing 4(4): 243-250.
2. Limwanich B (2011) Efficiency improvement of job scheduling by using genetic algorithm: a case study in electronic industry. Industrial Engineering and Engineering Management IEEE.
3. Sharma D (2013) Job scheduling algorithm for computational grid in grid computing environment. International Journal of Advanced Research in Computer Science and Software Engineering 3(5): 735-743.
4. Jaspher G, Kathrine W (2012) Job scheduling algorithms in grid computing-survey. International Journal of Engineering Research & Technology 1(7): 1-5.
5. Prajapati HB (2014) Scheduling in grid computing environment. IEEE.
6. Mei J (2014) A resource-aware scheduling algorithm with reduced task duplication on heterogeneous computing systems. The Journal of Supercomputing 68: 1347-1377.
7. Barbosa JMG (2009) Dynamic job scheduling on heterogeneous clusters. Parallel and Distributed Computing ISPDC.
8. Yadav K (2013) Job scheduling in grid computing. International Journal of Computer Applications 69(22): 13-16.
9. Skenteridou K (2015) Job scheduling in a grid cluster. IEEE.
10. Balajee M (2010) Premptive job scheduling with priorities and starvation cum congestion avoidance in clusters. Machine Learning and Computing, 2nd International Conference IEEE.
11. Chawla M (2016) Attitudinal data based server job scheduling using genetic algorithms: Client-centric job scheduling for single threaded servers. Contemporary Computing (IC3), 9th International Conference IEEE.
12. Mondal PK (2014) An approach to develop an effective job rotation schedule by using genetic algorithm. Electrical Information and Communication Technology.
13. Sakellariou R (2006) Job scheduling on the grid: towards sla-based scheduling. High Performance Computing Workshop 207-222.
14. Chang RS (2009) An ant algorithm for balanced job scheduling in grids. Future Generation Computer Systems 25: 20-27.
15. Tseng SP (2011) Job shop scheduling based on ACO with a hybrid solution construction strategy. Fuzzy Systems (FUZZ), IEEE International Conference.
16. Pandey S (2010) A particle swarm optimization-based heuristic for scheduling workflow applications in cloud computing environments, 24th IEEE International Conference on Advanced Information Networking and Applications, pp. 400-407.
17. Yang Y (2013) Heuristic scheduling algorithms for allocation of virtualized network and computing resources. Journal of Software Engineering and Applications 6: 1-13.