Chimera States - A Brief Introduction

The plethora of systems considered during the study of coupling between entities exhibiting nonlinear behaviour has led to the emergence of a new field of study encompassing biological science and mathematics, where the connectivity between neurones proves to be a worthwhile quest. But this is not restricted only to the above mentioned domains. In this respect, the one thing that interests the scientific community at large is the random presence of synchrony and its absence in a cluster of nonlinear systems. Any large scale complex network is capable of exhibiting this phenomenon. First observed by Kuramoto et al. [1-3] the phenomena mentioned here has got a very interesting name dating back to the time of Homer. Chimera - a three headed fire-breathing monster having the head of a lion, the body of a goat and the tail of a serpent - is the name given to this phenomenon.

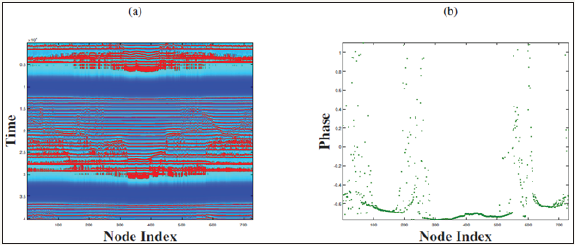
In a population of interconnected nonlinear systems identical in nature, the occurrence of chimera states can be indicated by simultaneous existence of coherent and incoherent states amongst different clusters of the population. The coherent oscillators have their phase locked and the incoherent ones are desynchronised amongst each other. The basic idea behind it was that, since the behaviour of the network as a whole cannot be termed as synchronous between its elements and neither can be termed as asynchronous, the confusion created is similar to that of a chimera as one cannot exactly classify the chimera as a particular animal. It should be kept in mind that similar phenomenon can be observed in the case of a population consisting of non-identical systems. But there as the asynchronous nature is attributed to the in homogeneity of the network, it cannot be termed as chimera. An example of the existence of chimera state in a population of similar nodes is shown in Figure 1.

This figure gives a superficial idea about how the chimera state might look like in a neural network consisting of about eight hundred nodes. The abcissa in Figure 1a is the node index and the ordinate is the one of the state variables. As can be seen, between the nodes three hundred and four hundred there is a continuum of the state variable thus indicating that the nodes are in sync with each other. This is further bolstered by the continuous line in Figure 1 showing that their phases are locked. Now that we have given a brief glimpse of what chimera states might look like in a homogeneous population of nonlinear oscillators, we are ready to point towards certain field of research where this concept has proven its use. This is given the next section.

Figure 1: One of the

1a: State variables of each node of a network and their corresponding

1b: Phase.

The experimental verification of the existence of chimera states has been widely studied. The areas researchers had focussed on are-chemical oscillators, mechanical oscillators, optical oscillators, electronic systems, electro-chemical oscillators and biological systems to name a few. In this section we try to discuss each of these important areas with brevity.

Chemical systems

In [4], the authors deal with two subpopulations of identical chemical oscillators (Belousov Zhabotinsky type oscillators) which are globally coupled and are coupled amongst the subpopulations. The coupling inside each subpopulation is stronger than that between the two subpopulations. On external perturbation via light, it has been observed experimentally that although one of the groups have constant synchronisation amongst its elements, the other one had synchronised as well as unsynchronised and semisynchronised states amongst its elements. The chimera state appeared to be asymptotically stable and if the system size increases then so does its occurrence. This might be because of the fact that the oscillators used in this experiment are of relaxation type. This state would not have occurred of the coupling was only global. These type of observations were also reported in [5].

Mechanical systems

The simplest example of a mechanical nonlinear system is the pendula. In [6], the authors have considered a collection of Huygen’s clock (twenty in number) to exhibit the existence of chimera as well as ‘imperfect chimera’ states. Numerical simulations have also been done considering a hundred coupled pendula and the results have shown correlation with those obtained from the experiments. Experiments with similar systems have been done in [7] to show that in two subpopulations of metronomes1 coupled with mere springs can exhibit chimera states with the sole variation of the coupling strength.

Optical systems

In [8], using a a liquid-crystal spatial light modulator to achieve optical nonlinearity in a spatially extended iterated map system, the authors have been able to study the coherence and incoherence in a population of similar nonlinear oscillators, which are inherently responsible for the emergence of chimera states.

Electronic systems

A more complex nature of nonlinear system is exhibited by those which mimic the spiking of neurones. In this respect, the authors of [10] have used the FitzHugh-Nagumo (FHN) neuron coupled with its nearest neighbors in a chain configuration to experimentally demonstrate that chimera states appear without any fine-tuning of both the coupling and oscillator parameters. It has also been shown that the chimera states emerge with quiescent and synchronous domains when the position of the circuit in the chain was varied.

Electrochemical systems

Electrochemical systems like the tank reactor have been used to observe chimera states. In [11], a network of electrochemical systems has been constructed where each node is an oscillatory nickel dissolution reaction occurring on the surface of an electrode of an array of electrodes. Consisting of a total of one hundred and forty connections, this network was able to exhibit chimera states when the coupling was varied [12,13].

Biological systems

All the above examples discussed have considered systems which help in idealising a controlled environment in order to stody effective dynamic characteristics. However, they are not that tangible in day to day life. But when it comes to physiological processes like the circadian rhythms or neuron electrophysiology things become more interesting as with these we are able to relate on different levels. It was revealed by a study on Diffusion Tensor Magnetic Resonance Imaging that the connectivity between the neurones in a mammalian brain (also human) has a hierarchical structure [14-18]. Naturally the scientific community dealing with studies relating to chimera dug deeper in order to see whether these systems exhibit chimera like states under global and local coupling. In this respect, the Hindmarsh Rose neurone model found popularity. One such work is [19], where chimera like states has been observed in modular networks.

So we have tried to give a short introduction to chimera states with utmost breivity. But what has not been included here are the ways in which chimera states can be controlled so as benefit for their appearance. One might imagine that since such states occur in complex networks of homogeneous population, it can have primal importance in the field of electrical networks like power grids, social network analysis as well as the much pursed neural networks.

FOOT NOTE

• ¹A variant of Huygen’s clock.

1. Kuramoto Y, Battogtokh D (2002) Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlinear Phenomena in Complex Systems 5(4): 380-385.
2. Kuramoto Y (2002) Nonlinear dynamics and chaos: where do we go from here? CRC Press, pp. 1-376.
3. Shima S, Kuramoto Y (2004) Rotating spiral waves with phaserandomized core in nonlocally coupled oscillators Physical Review E 69: 036213-036222.
4. Mark RSK, Simbarashe N (2012) Chimera and phase-cluster states in populations of coupled chemical oscillators. Nat Phys 8: 1-9.
5. Nkomo S, Tinsley MR, Showalter K (2013) Chimera states in populations of nonlocally coupled chemical oscillators. Phys Rev Lett 110: 244102.
6. Martens EA, Thutupalli S, Fourrire A, Hallatschek O (2013) Chimera states in mechanical oscillator networks. Proceedings of the National Academy of Sciences 110(26): 10563-10567.
7. Tomasz K, Patrycja K, Jerzy W, Krzysztof C, Yuri M (2014) Imperfect chimera states for coupled pendula. Scientific Reports 4: 6379.
8. Aaron HM, Thomas ME, Rajarshi R, Philipp H, Iryna O, et al. (2012) Experimental observation of chimeras in coupled-map lattices. Nat Phys 8: 658-661.
9. Larger L, Penkovsky B, Maistrenko Y (2013) Virtual chimera states for delayed-feedback systems. Phys Rev Lett 111: 054103.
10. Gambuzza LV, Buscarino A, Chessari S, Fortuna L, Meucci R, et al. (2014) Experimental investigation of chimera states with quiescent and synchronous domains in coupled electronic oscillators. Phys Rev E 90: 032905.
11. Wickramasinghe M, Istvan ZK (2013) Spatially organized dynamical states in chemical oscillator networks: Synchroniza-tion, dynamical differentiation, and chimera patterns. Plosone 8(11): 11.
12. Wickramasinghe M, Istvan ZK (2014) Spatially organized partial synchronization through the chimera mechanism in a network of electrochemical reactions. Phys Chem Chem Phys 16(34): 18360-18369.
13. Schmidt L, Schonleber K, Krischer K, Garc´ıa-Morales V (2014) Coexistence of synchrony and in-coherence in oscillatory media under nonlinear global coupling. Chaos: An Interdisciplinary Journal of Nonlinear Science 24(1): 013102.
14. Katsaloulis P, Vergsnelakis DA, Provata A (2009) Fractal dimension and lacunarity of tractography images of the human brain. Fractals 17(2): 181-189.
15. Expert P, Tim SE, Vincent DB, Lambiotte R (2011) Uncovering spaceindependent communities in spatial networks. Proceedings of the National Academy of Sciences 108(19): 7663-7668.
16. Katsaloulis P, Ghosh A, Philippe AC, Provata A, Deriche R (2012) Fractality in the neuron axonal topography of the human brain based on 3-d diffusion mri. The European Physical Journal B 85(5): 150.
17. Katsaloulis P, Hizanidis J, Vergsnelakis DA, Provata A (2012) Complexity measures and noise effects on diffusion magnetic resonance imaging of the neuron axons network in the human brain. Fluctuation and Noise Letters 11(4): 1250032.
18. Provata A, Katsaloulis P, Verganelakis DA (2012) Dynamics of chaotic maps for modelling the multifractal spectrum of human brain diffusion tensor images. Chaos, Solitons & Fractal 45(2): 174-180.
19. Hizanidis J, Kouvaris NE, Zamora L, Guilera G, Antonopoulos CG (2016) Chimera-like states in modular neural networks. Scientific Reports 6: 19845.