Maximizing the Intermediate Product for 3 CSTRs in Series

A complete and fundamental understanding of conversion in CSTRs and PFRs in mixed configurations is essential to minimizing operational and capital input costs. Recently, researchers have been exploring analytical models to determine the concentrations in increasingly complex reactor and reaction systems [1-11]. One key reaction of interest is the oxidation of an alcohol to a carbonyl product and subsequent conversion to waste CO₂.

ROH + Air− > RCHO + Air− > CO₂ + H₂O

simplified as R− > P− >W

The residence time for this system to achieve maximum conversion to P in a single CSTR is widely reported for the case of series reactions, R->P->W, as [1,2]:

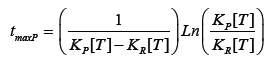
By fixing the space time, and altering either volume or temperature the reaction will progress such as to shift around this critical time. Determining the volumes and temperatures associated with maximum conversion to the useful product is nontrivial and of vital importance. Find methods to theoretically determine this temperature such that startup capital and operational costs can be reduced. This leads to decreased flow rate and increased total product made.

Therefore, Mathematica is utilized to apply analytic and numerical approaches in determining the best temperature and volume configuration for specific relative rate constants in the 2CSTR case and varied volumes in the 3CSTR case. The reactions discussed in this document are assumed to occur isothermally, adiabatically and incompressibly.

Figure 1: The concentration of each species in a chain of series reactions as a function of time [3].

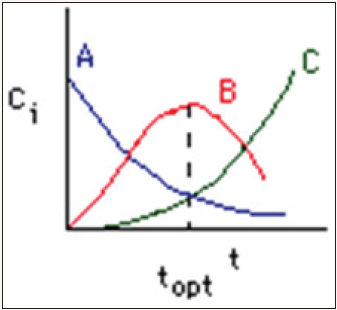
Considering 3 CSTRs in series operating at the same temperature with assumed isothermal, adiabatic and incompressible behavior, this study explores the conversion to product P at the outlet of the third CSTR. An alternative to this design is a single large reactor, which is often not preferred because conversions of single CSTRs with volumes similar to the total volume of this analysis are lower than this 3CSTR design. Additionally, increasing the conversion of the single CSTR reactor to decrease space time would require more

than triple the flow rate and result in increased capital costs in the form of a larger, more expensive pump and operating costs in the form of power consumption. For reasonably viscous systems, this is a significant disadvantage.

Let the flow rate through the system be 7.5L/min, the rate constant of the first reaction be k_R=0.1min-1, the constrained volume of the system be V_tot=100L; and the inlet concentration of the species be c_R,0=1mol/L and c_P,0=c_w,0=0mol/L. Let “a” be a factor that inter-relates k_P and k_R (a=k_P/k_R), and w be the volume of the third CSTR (w=V_tot-V₁-V₂) such that an expression for the concentration of product P at the outlet of the third CSTR is given by:

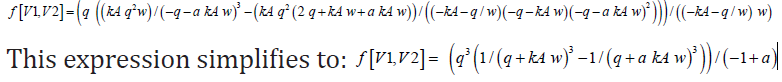
Figure 2: k_P/k_R=700, k_p/k_R=30.

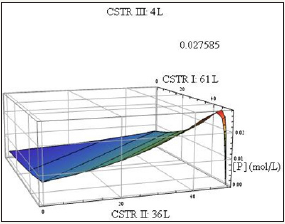
Figure 3: k_P/k_R=1, k_p/k_R=0.5

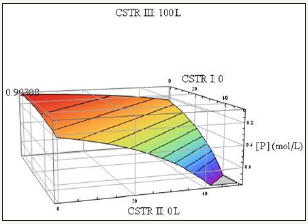
Determination of the maximum value on the conversion curve analytically for arbitrary rate constant ratio and volume configuration requires a Lagrange multipliers approach. This method was applied in this study to determine such a value which is indicated on the following plots. The values on the ordinates specify the volume of the reactor associated with the maximum conversion (Figure 2 & 3). An important consideration in multiple CSTR design is the configurational order of the CSTRs. For gas reactions occurring at non-negligible density change (with a nonzero difference between moles formed and reacted) the volumes will be non-interchangeable since the spacetimes associated with equal volume CSTRs will vary as the flow rate varies with the ordering. For liquid phase reactions, however, a given configuration (V1,V2,V3) can be rearranged will less of an impact.

It is theoretically possible to maximize conversion further then presented in two CSTRs case and three CSTRs case by varying reactor volume and relaxing the constraint that the reactors operate at the same temperature. The analysis for 3 CSTRs can be performed at arbitrary temperatures by calculating the ratio k₂/k₁ at a specific temperature and then utilizing the conversion vs. volume configuration plots.

For a given kinetic expression, the conversion maximization problem was solved in terms or ratios of fundamental rate constants and activation energies for the two CSTRs in series case. There is a key optimal temperature to run both reactors at to maximize conversion. Then the conversion was maximized for three CSTRs in series by changing the relative rate constants and applying a Lagrange multiplier approach.

1. Fogler S (1999) Elements of chemical reaction engineering, (3rd edn), Prentice Hall, Upper Saddle River, NJ, USA, pp. 440, 504, 537, 553, 566.
2. Davis, Mark E, Davis, Robert J (2003) Fundamentals of chemical reaction engineering. McGraw-Hill Higher Education, New York, USA.
3. http://www.engin.umich.edu/~cre
4. Mathematica tutorial collection in chemical engineering.
5. http://demonstrations.wolfram.com/MaximizingConversionToAnIntermediateProductInATwoStageCSTR/
6. http://demonstrations.wolfram.com/MaximizingConversionToAnIntermediateProductInAChainOfThreeCS/
7. http://demonstrations.wolfram.com/DynamicsOfANonadiabaticContinuouslyStirredTankReactor/
8. Tsangaris DM (1999) On the behavior of consecutive enzymatic reactions in cyclically operated reactors. Chem Eng Comm 176(1): 229-246.
9. Thomas S, Pushpavanam S, Morgenstern AS (2004) Performance improvements of parallel-series reactions in tubular reactors using reactant dosing concepts. Industrial & Engineering chemistry Research 43(4): 969-979.
10. Baltis BC, Lewandowski GA, Sanyal S (1991) Sequencing batch reactor design in a denitrifying application. ACS Symposium Series 468: 282- 300.
11. Tsangaris DM, Baltzis BC (1996) Evaluation of batch and semi-batch reactor operation for enzymatic reactions with inhibitory kinetics. Chemical Engineering Science 51(11): 2757-2762.