Numerical Simulation of Three-Dimensional Processes of the Interaction of Elastic-Plastic Bodies with the Product of Detonation in Eiler Variables

Experimental and theoretical investigation of the processes of interaction and acceleration of deformable solid elasto-plastic bodies with the products of detonation is a complex spatial problem. Interaction with the detonation wave can cause stresses in the elastoplastic body, which considerably exceed the yield strength and substantially deform it during the contact. This process of deformation is very short and, in fact, detonation products can accelerate the body whose shape varies significantly and differs from the initial one. With the development of computer technology, it became possible to simulate these processes numerically. When solving such problems, it is necessary to take into account the processes of initiation and propagation of detonation in solid explosives with the generation of shock waves by expanding explosion products and their interaction with elastoplastic bodies, significant deformation and displacement of these bodies.

The solution of such problems even in simplified statements is possible only numerically and requires considerable computational resources. In this paper, a three-dimensional program complex developed by the authors [1] based on the use of three kinds of grids is used to model these processes. This is a grid in the form of sets of triangles (STL files) that define the surfaces of interacting bodies and trace these surfaces in the solution process, as well as a basic Cartesian fixed grid embedded in each body, and local mobile grids tied to each triangle of the body surface. To solve the Euler equations of the gas-dynamic part and Euler-Cauchy for elastoplastic flows, a modification of the Godunov difference scheme of increased accuracy [2] is used. To describe the process of propagation of detonation, the time-dependent model of detonation generalized to the three-dimensional case is used [3]. For detonation and air products, the equation of state of type JWL [4] is used, the boundary between products of detonation and air is not traced, and generalized Hooke’s law is applied for the elastic behavior of the material, taking into account the plastic behavior of the material in accordance with [5].

In Figure 1 the statement of the problem is shown. Charge of TG36/64 of the spherical shape, radius 5cm, the source of initial detonation was set in a region of radius less than 0.2cm. The cross section passes through the center of the charge and the centers of the cubes. In the charge and the air the main grid was used with the side of the cubic cell 0.15cm. Three steel cubes with side 1cm are marked with red, material steel 3, weight 7.8grams. Step of the main grid in cubes is 0.07cm. Figure 2 shows the density distribution at the time of 55μs, in Figure 3-the shape of the cubes, respectively, at the initial moment and at 55μs. The cubes are strongly and irreversibly deformed, the streams of detonation products move much faster, and gas jets are formed around the cubes. Figure 4 shows the speed on the surface of the cube, accelerated in the vertical direction, the lower curve corresponds to the center of the upper (far from the charge) surface, respectively, the upper curve to the center of the lower (near to the charge) surface of the cube.

Figure 1: The statement of the problem.

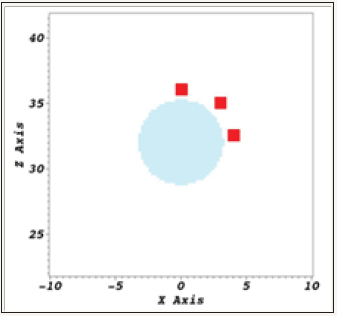
Figure 2: Density at 55μs.

Figure 3: Final forms of cubes.

Figure 4: Velocities on the opposite side of cube.

The following bodies of the equal mass of 0.92 grams of the same steel, but of different shapes, were also considered. These are tetrahedrons with a side of 1cm, disks with a diameter of 1cm, a height of 0.15cm and cubes with a side of 0.49cm, located at the same points.

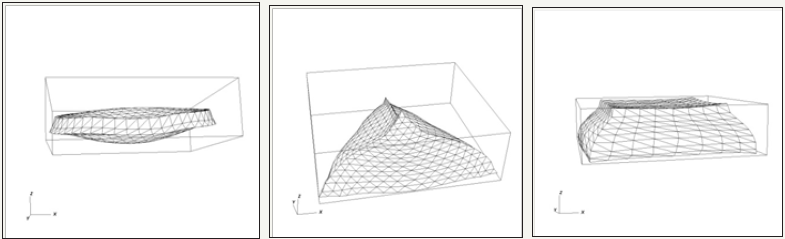
Figure 5 shows the dependence of the velocities of the center of mass on time for the disk (mark 1), tetrahedron (mark 2) and cube (mark 3), accelerated along the vertical axis. Dashed lines indicate these dependencies, calculated in an elastic formulation. The essential dependence of speed on the geometry of the bodies and the change in shape during acceleration is obvious. The duration of the acceleration time of the body is comparable with the time of detonation wave exit to the contact surface. The basic residual deformations that change the geometry of the bodies occur at the initial stage of acceleration. In Figure 6 shows the residual forms of these bodies.

Figure 5: Velocities of different form bodies of the same mass.

Figure 6: Final forms of different bodies of the same mass.

1. Abuziarov KM, Abuziarov MH, Kochetkov AV (2016) 3D fluid structure interaction problem solving method in euler variables based on the modified godunov scheme. Materials physics and mechanics 28(1/2): 1-5.
2. Abouziarov M, Aiso H (2006) An application of retroactive characteristic method to conservative scheme for structure problems (elasticplastic flows). Hyperbolic Problems, Theories, Numerics, Applications. Yokohama Publishers, Japan, pp. 223-230.
3. Abuziarov MH, Kochetkov AV, Krylov SV, Tsvetkova EV (2008) Numerical simulation and the effects of gas-cumulative charges on the barriers. Computational mechanics of continuous media 1(2): 5-15.
4. Orlenko LP (2002) Physics of the explosion. Fizmatlit 2(3): 656.
5. The method of splitting of elastoplastic equations. Kukujanov VN (Ed.), Izvest, Russia.