Radiative Heat Transfer in the Chemically Reactive Unsteady MHD Squeezed Flow of Second Order Fluid with Heat Source

Introduction

It is a critical issue of modern world to develop the new techniques for renewable energy. The main sources of renewable energy are solar energy, hydropower, fossil fuel and wind. The heat and electric energies can be produced by the natural source in the form of solar radiation and solar powers. Moreover, radioactive heat transfer play a vital role in science and technology such as heating and cooling chamber, rivers, canals, dams, food processing, textile engineering and many other industrial processes. Many researchers [1- 5] are developing new energy sources and technologies of renewable energy. In addition, most of the computer system and electrical powers dissipate the heat energy therefore heat source and sink are important for the reliable performance of electronic operators. For a number of heat source/sink problems studies are investigated by a number of researchers [6,7]. Chemical engineering requires new techniques consisting of material manufacture and polymers in bioreactors in medical biotechnology.

The dynamics of biofluids exhibit the characteristics of thermofluid for which the mass transfer is the vital agent of bioreactor design. The fluid dynamics of such system shows the heat and mass transfer effects in confined boundaries such as fire dynamics, fuel cells and solar cell technologies. Effect of chemical reaction and heat source on heat and mass transfer have been discussed by various investigators, e.g. Muthucumaraswamy et al. [8,9] studied the unsteady upward flow of viscous fluid with chemical reaction and heat source on an isothermal and oscillating plate. Saxena SS & Dubey GK [10] discussed the effect of heat and mass transfer for the flow of viscoelastic fluid with heat source, thermal radiation and slip boundary conditions. Ibrahim et al. [11,12] discussed the impact of heat source and chemical reaction on viscous fluid passed through a porous regime with Joule heating and viscous dissipation later he has extended these effects on unsteady MHD flow of viscoelastic fluid. Noreen SA et al. [13] discussed the radiative heat and chemically reactive mass transfer of MHD peristaltic flow of Maxwell fluid in a symmetric channel through a porous medium. The work of Hayat et al. [14] analyzed the unsteady axisymmetric squeezed flow of Jeffrey fluid between parallel plates under the radiation effect. The heat and mass transfer analysis of MHD second grade fluid in the presence of thermal radiation and diffusion is carried out by Olajuwon et al. [15]. Recently, group theoretical method to study the similarity solution of convective heat and mass transfer flow for MHD Newtonian fluid with convective boundary conditions is studied by Rashidi et al. [16,17] also studied thermal convective boundary conditions and hydrodynamic slip conditions of convective heat and mass transfer flow along a plate kept in vertical direction.

Squeeze flows may observe between two parallel rectangular or circular plates; however the squeeze motion depends on the geometry of the surface. In squeeze flows solid or liquid is compressed between two disks and is thus squeezed out. Squeeze flows are investigated in different field of research e.g. geophysics, material science, biotechnology, engineering science and fluid mechanics.

In 1874 Stefan et al. [18] first considered reverse squeeze flows for the Newtonian fluid, later in 1886, Reynolds [19] obtained the results for the predictable squeezed flow for the Navier Stokes equation under the lubrication approximation. Scott [20] extended the Reynolds’ idea for the non-Newtonian fluid showing the shear thinning and thickening effects for the creeping flow. It is analyzed from the literature review that analytic solutions for axisymmetric and plane squeezed flow for viscous and viscoelastic fluids are discussed by various researchers [21-29]. In addition some other researchers studied the thermo dynamic effects of squeezed flow like Khaled & Vafai [30] discussed heat transfer effect for the squeezed flow of viscous fluid on a sensor surface. Mahmood et al. [31] presented heat transfer analysis of squeezed flow on a porous surface. Squeezed flow and heat transfer analysis between two plates was considered by Duwairi et al. [32]. Recently, Mustafa et al. [33] addressed the heat and mass transfer of squeezing flow of Newtonian fluid through a rectangular channel. Khan et al. [34] has compared the analytic solution of viscous fluid for the axisymmetric flow in a slip regime. Ganji et al. [35] discussed the analytic solution of squeezed flow with magnetic effects between two porous plates by Homotopy analysis method, he has also compared the results for suction and blowing cases by Homotopy perturbation method.

The broad aim of present work is to analyze the radiative heat and mass transfer flow of MHD second order fluid between two parallel discs with chemical reaction and heat source subjected to squeezing system. The similarity transform method is used to transform the system of partial differential equations into ordinary differential equations. Numerical technique (Advanced collocation Method) is used to solve the ordinary differential equations governing the fluid flow, pressure distribution, concentration and temperature profile.

Problem Formulation

Let us consider an unsteady axis symmetric squeezing flow of second order fluid between two parallel circular plates moving with speed

and distance between both plate is

where is the characteristic time parameter. A constant magnetic

is applied transverse to the plates. The induced magnetic field can be neglected due to the small magnetic Reynold’s number. The plates move symmetrically about radial direction while flow is axisymmetric about the axial direction. The temperature and mass concentration on the lower plate are T₀ and C₀ while T_h and C_h are temperature and concentration on the upper plate as shown in Figure 1.

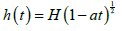
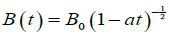
Figure 1:Schematics diagram of the problem.

The governing mass, momentum, energy and diffusion laws for second order/grade fluid can be stated as

divV = 0, (1)

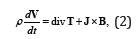
where

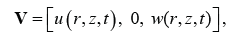
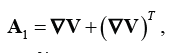
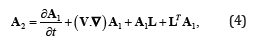
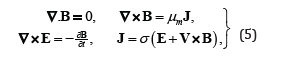
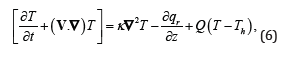
where

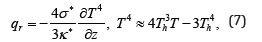
and

The B.C’s on velocity, temperature and concentration profile are

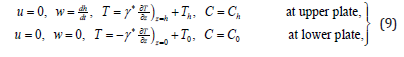
where is the radial velocity, w is the axial velocity, C and are the concentration and temperature profile respectively.ρ , μ, σ , κ , D_m Qand R are the density of the fluid, viscosity of the fluid, electrical conductivity, thermal diffusivity, diffusivity constant, heat source parameter and chemical reaction parameter respectively.

are second order/grade fluid parameters, 1 A is the first RivlinEricksen tensor J is the current density ε is the electric field and due to no polarization effect E = 0, σ is the Stefan constant and k_m mean absorption coefficient and γ ^∗ is thermal slip parameter.

Let us define following parameters

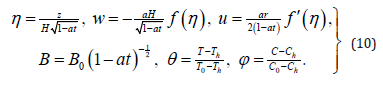
In view of equation (10) the governing laws and boundary conditions in Eqs.(1)-(9) reduce to

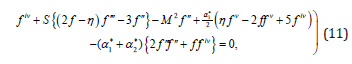
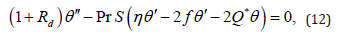
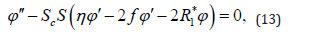
subject to the B.C’s

where

In order to find the pressure distribution using Eq. (10) in Eqs. (2)-(5), we get the following expression

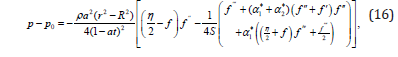
where P is the modified pressure and P0 is the reference pressure.

The pressure on the upper plate is given in the following form

The important characteristics of velocity, heat and mass transfer are the skin friction coefficients , c_frh Nusselt number Nu and Sherwood number S_h and are defined as follows

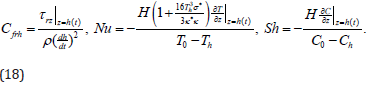
The wall shear stress, skin friction coefficient, Nusselt number and Sherwood number in non-dimensional form are given by the following expressions

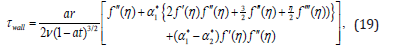
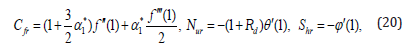
where

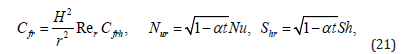
in which

denotes the local Reynolds number, C_fr is the skin friction coefficient at the upper plate, N_ur is the heat transfer rate on the upper plate and S_hr is the mass concentration rate on the upper plate.

Numerical Solution

We have successfully transformed the governing partial differential equations (PDE’s) to ordinary differential equations (ODE’s) with the use of similarity transform method. We have solved the transformed equations (11-14) subject to boundary conditions in Eq. (14) numerically using an advanced collocation method. This mathod is useful because, it reduces the nth order differential equation(s) into first order differential equations, thus reducing the computational cost on a large domain with small step size and a range of parameters. We have simplified the system of equations (11-14) using the Modified Collocation Method (CM). The use of polynomial or piecewise polynomial collocation spaces for the approximate solution of BVP has its origin in the 1930s. Khater et al. [38] much later elaborated a spectral collocation method (SCM) based on differentiated Chebyshev polynomials to find numerical solutions for nonlinear partial differential equations (PDE’s). They reduced the nonlinear equations to the system of ordinary differential equations and solved by Runge--Kutta Method of order four (RK4).

Therefore the key role of this method is that, it reduces the order differential equation(s) into first order differential equations, thus reducing the computational cost on a large domain with small step size and a range of parameters. We have simplified the system of equations (11)-(14) using the Modified Collocation Method (CM). The collocation solver [38] when applied to the BVP produces continuous solution on an appropriate mesh.

For a general BVP defined on the interval [x0,xm] subject to two-point boundary conditions, bvp4c implements a Collocation Method (CM) for the solution of Boundary Value Problems of the form:

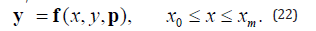
subject to nonlinear B.C’s

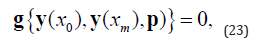
where p is a vector of unknown parameters. The numerical solution W(x) encompasses a continuous functions which is a polynomial of order three on each subinterval [x_i,x_i+1] of the finite difference grid (mesh) defined by:

satisfying the associated boundary conditions.

Furthermore it satisfies the nodes at both (left and right) ends and the middle of each sub-interval

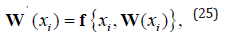
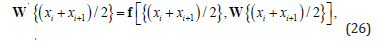
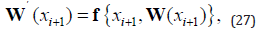
The above conditions generate a robust family of non-linear algebraic equations for the coefficients defining W(x) . Distinct from shooting algorithms, the solution y(x) is approximated on the domain [x₀, x_m] The boundary conditions are considered at all stages of the computations. The nonlinear algebraic equations are iteratively solved via linearization and this is achieved via the linear equation solvers in MATLAB, and not the IVP solvers. Essentially the bvp4c algorithm is a modified Simpson stepping scheme and W(x) is a fourth order approximation to an isolated solution y(x) , viz:

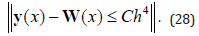
Here designates the maximum number of step sizes h_i = x_i+1-x_i , and C is a constant. This bound is enforced for all x in [x₀, x_m] . Following computation of W(x) on the mesh with bvp4c, it is updated and improved quickly and cost-effectively at any x or set [x₀, x_m].

To be more precise, the obtained collocation solutions to the system of ordinary differential equations (11-14). Thus we used a finite difference code that construct a collocation formula and the collocation polynomial gives a continuous solution in the domain [36]. The Iterative method is used to solve the linearized nonlinear algebraic equations, so this method relies upon Matlab solver of the linear equation. The choice of max η =1 guaranteed that all numerical solutions approached the asymptotic values correctly, although the finite choice of max η will be not fully responsible for minimized order of accuracy, such as Kuznetsov & Nield [37] & Sohail et al. [39] compared their results for the special case of a regular fluid with their numerical results obtained by keeping max η =10 , and ignored the error generated by limiting the domain, in a similar manner, we will ignore that error.

Numerical Results and Discussion

Here we discussed the effect of pertinent parameters on the velocity profile, temperature profile, concentration profile skin friction coefficient, local Nusselt number and local Sherwood number.

Figure 2:Influence of squeezing parameter S on f (η ) and f ′(η )

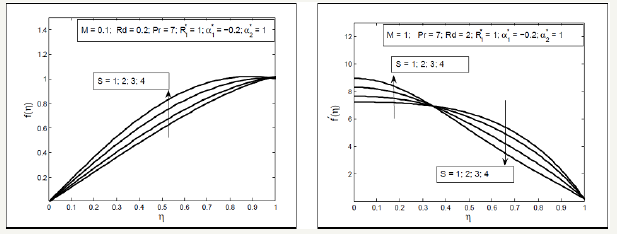
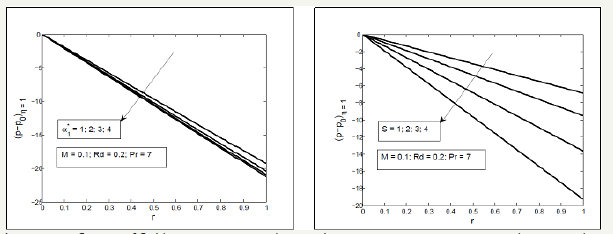
Effect of Squeezed number S on the radial and axial velocity f ′(η ) and f (η ) have been analyzed through Figure 2. It is analyzed that the radial velocity f ′(η ) decelerate near the upper plate and enhances near the lower plate and axial velocity f (η ) accelerate between two plates with the increase in Squeezing parameter S . Effects of magnetic parameter can been seen through Figure 3, it is depicted that the axial velocity f (η ) slow down with the increase in Hartmann number M but the radial velocity shows the f ′(η ) dual behavior first decreasing then increasing. In fact the magnetic field acts along the axis that resist the fluid motion consequently the axial velocity decreases also the radial velocity near the lower plate decelerate due to Lorentz force but near the above plate the squeezing effects are dominant therefore the velocity increases. Figure 4 display the effects of fluid parameters It is seen from the figures that increasing values of parameters causes to increase the viscosity of the fluid so the axial velocity decreases but the radial velocity near the upper plate enhances as the upper plate moves towards the lower stationary plate. Variation of thermal slip parameter γ and squeezed number S on the temperature profile is shown in Figure 5. It is observed that temperature θ (η ) profile enhances near the lower plate and decreases near the upper plate for higher thermal slip parameter. It is due to the fact that the lower plate provides thermal conductivity whereas the upper plate provides large amount of thermal resistance which consequently decelerate the temperature distribution. The higher value of squeezing parameter shows the increase in temperature profile away from the lower plate but on the lower plate temperature profile decreases due to thermal slip. Increasing values of squeezing parameter illustrate that viscosity decreases as the distance between two plate’s increases. Figure 6 is plotted for different values of Prandtle number Pr and heat source parameter (Q^∗ ) to illustrate the impact of Pr and Q^∗ on temperature profile. It is observed that increasing value of Pr causes to reduce the thermal conductivity of the fluid away from the lower plate due to which the temperature profile decreases. The increasing value of heat source parameter Q^∗ causes to accelerate the rate of heat transfer thus it enhances the temperature profile. Figure 7 shows the impact of magnetic parameterM and radiation parameter d R on temperature profile, it is observed that temperature profile decrease with the increase in magnetic parameter as it resist the motion of the fluid so the fluid become thick and thermal conductivity decreases so the temperature profile decelerate while the radiation parameter enhances the heat transfer. Figure 8 show that the decrease in fluid parameter thermal conductivity near the lower increases therefore the temperature profile increases but near the upper plate thermal conductivity reduces so the temperature profile decelerate also the concentration profile near the lower plate increases due to increase in Schmidt number and decreases near the upper plate i.e. viscous diffusion rate enhances the mass concentration near the lower plate but near the upper plate the squeezed effect are strong as compared with the viscous diffusion rate therefore mass concentration decelerate Figure 9 shows the influence of chemical reaction parameter ( 1 R^∗ ) and squeezing parameter ( S ) on the concentration profile. It is depicted from the plots that the chemical reaction parameter causes to increase the mass concentration of the fluid also squeezing parameter show the increasing behavior of the concentration profile.

Figure 3:Influence of Hartmann number M on f (η ) and f ′(η )

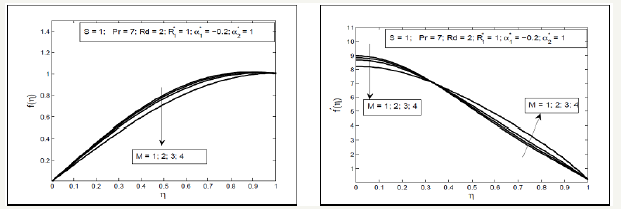
Figure 4:Influence of second grade parameter 1 a ∗ on f (η ) and f ′(η )

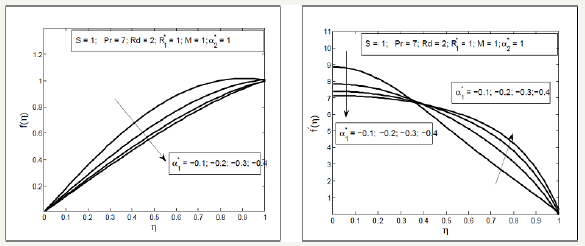
Figure 5:Influence of thermal slip parameter γ and squeezing parameter S and θ (η

Figure 6:Influence of Prandtl number Pr and heat source parameter on θ (η ).

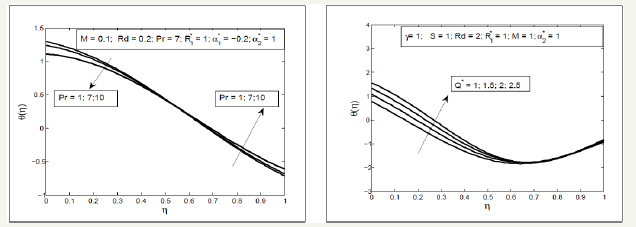
Figure 7:Influence of Hartmann number M and radiation parameter Rd on

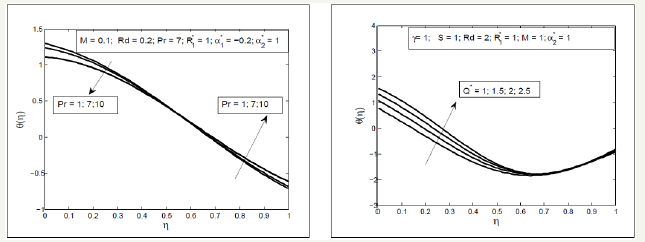
Figure 8:Influence of second order parameter on θ (η ). and Sc on ϕ (η ).

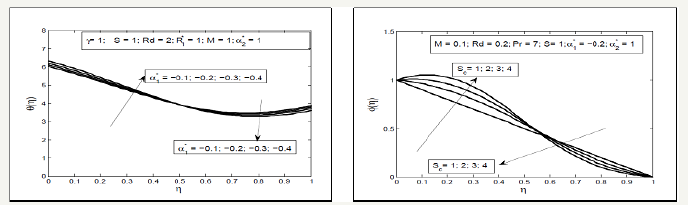
Figure 9:Influence of chemical reaction parameter R1* and squeezing parameter S on ϕ (η

Figure 10:Influence of Hartmann number M on skin friction coefficient Cfrand chemical reaction parameter R1*on Schmidt number SC.

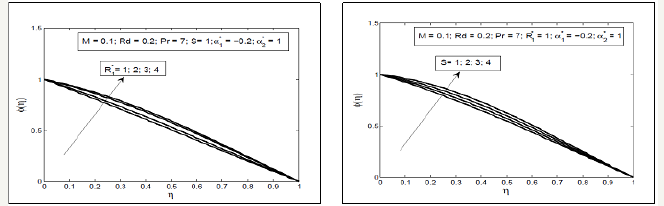
Figure 11:Influence of heat source Q∗ and thermal slip parameter γ on Nusselt number Nu.

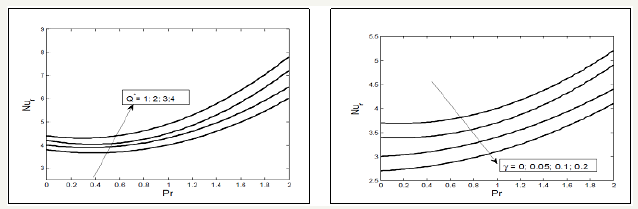
Figure 12:Influence of fluid parameter a1* and squeezing parameter S on pressure at the upper plate..

The skin friction plays an important role in thermal and engineering processes, since it is the friction between the surface of a moving solid through a fluid and the fluid itself. It is depicted from Figure 10 & 11 that skin friction at the upper plate increases with the increase in magnetic parameter while for large value of squeezing parameter skin friction decreases. Nusselt number ( Nu ) is defined as the rate of heat transfer at the surface when a fluid past through a solid surface. It is observed that the Nusselt number shows the increasing behavior with the increase in heat source parameter Q^∗ but it decreases with the increase in thermal slip parameter also Nusselt number increases for the large values of Prandtl number. Further, it is seen that the Sherwood number ( Sh ), is the rate of mass transfer at the surface and it decreases for the large values of chemical reaction and increases for large Schmidt number.

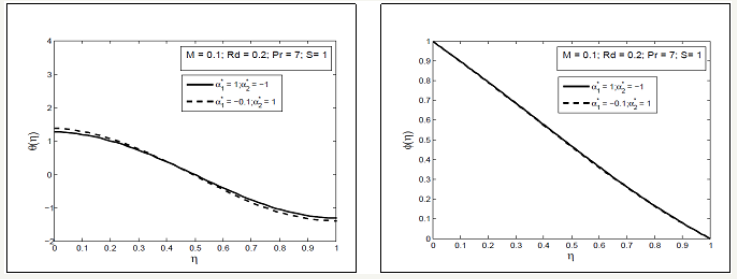
Figure 12 illustrate that the pressure on the upper plate increases in negative direction with the increase in the fluid parameter and squeezing parameter i.e. the squeezing velocity and fluid parameter produce the much pressure on the upper plate in reverse direction as compared with the lower plate. The comparison of second grade and second order fluid parameter is shown for the velocity, temperature and concentration profile through Figure 13 & 14. It is seen through these figures that axial velocity is greater for the second order fluid as compared with the second grade fluid while radial velocity for the second order fluid is greater near the lower plate but smaller near the upper plate as compared with the second grade fluid. Temperature profile near the lower plate is greater in second order fluid as compared with the second grade fluid while reverse near the upper plate. Concentration profile is same for both second grade and second order fluid.

Figure 13:Comparison of second grade and second order fluid for the velocity profile.

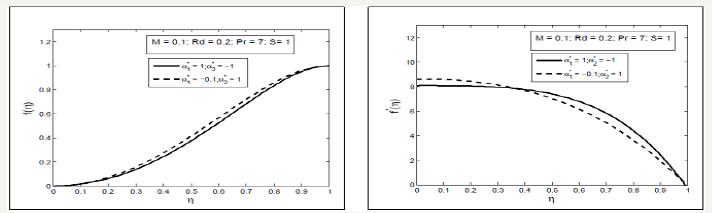
Figure 14:Comparison of second grade and second order fluid for the temperature and concentration profile.

Conclusion

In this paper we have presented a numerical approach to study heat source and chemical reaction of radiative unsteady MHD squeezed flow of second order fluid under the effect of thermal boundary conditions. The axisymmetric squeezed flow is induced by time dependent motion of parallel plates. Radiative squeezed flow of Newtonian and non-Newtonian fluids with heat source and chemical reaction under the convective boundary condition is a current topic of interest. Different studies exist in literature in which the squeezed flow in different geometries discussed [19,21,24,25].

In the present study we have concluded the following observations

a. Effect of squeezing parameter S on axial velocity f (η ) is opposite to that of second order fluid parameters and Hartmann number M .

b. Large values of squeezing parameter S second order fluid parameters and magnetic parameter M on radial velocity f ′(η ) shows the dual behavior.

c. Temperature distribution shows the mixed behavior for larger heat source Q^∗ , squeezed number S , Prandtl number Pr and thermal slip parameter

d. Mass concentration increases by increasing squeezing parameter S and chemical reaction parameters

e. Skin friction coefficient decreases for higher values of magnetic parameter M whereas increases for large values of squeezing parameter S

f. Nusselt number ( Nu ) enhances for large values of heat source parameter Q^∗ and Prandtl number Pr but decreases for large values of thermal slip parameter γ .

g. Sherwood number ( Sh ) accelerate for large values of Schmidt number Sc and decelerate for the large values of chemical reaction parameter R₁^∗

h. Pressure on the upper plate increases in negative direction with the increase in the fluid parameter and squeezing parameter S .

i. Axial velocity is greater for the second order fluid as compared with the second grade fluid while radial velocity for the second order fluid is greater near the lower plate but smaller near the upper plate as compared with the second grade fluid.

j. Temperature profile near the lower plate is greater in second order fluid as compared with the second grade fluid while reverse near the upper plate.

k. Concentration profile is same for both second grade and second order fluid.

References

1. Hussanan A, Anwar MI, Ali F, Khan I, Shafie S (2014) Natural convection flow past an oscillating plate with Newtonian heating. Heat Transfer Research 45(2): 119-135.
2. Makinde OD (2005) Free convection flow with thermal radiation and mass transfer past a moving vertical porous plate. International Communications in Heat and Mass Transfer 32(10): 1411-1419.
3. Ibrahim FS, Elaiw AM, Bakr AA (2008) Influence of viscous dissipation and radiation on unsteady MHD mixed convection flow of micropolar fluids. Appl Math Inf Sci 2(2): 143-162.
4. IDas K (2012) Impact of thermal radiation on MHD slip flow over a flat plate with variable fluid properties. Heat and Mass Transfer 48(5): 767- 778.
5. Touahri S, Boufendi T (2015) Conjugate heat transfer with variable fluid properties in a heated horizontal annulus. Heat Transfer Research 46(11): 1019-1038.
6. Pal D, Chatterjee S (2010) Heat and mass transfer in MHD non-Darcian flow of a micropolar fluid over a stretching sheet embedded in a porous media with non-uniform heat source and thermal radiation. Communications in Nonlinear Science and Numerical Simulation 15(7): 1843-1857.
7. Chamkha AJ, AlyAM (2010) MHD free convection flow of a nanofluid past a vertical plate in the presence of heat generation or absorption effects.Chemical Engineering Communications 198(3): 425-441.
8. Muthucumaraswamy R, Ganesan P (2001) Effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate. Journal of Applied Mechanics and Technical Physics 42(4): 665-671.
9. Muthucumaraswamy R, Janakiraman B (2008) Mass transfer effects on isothermal vertical oscillating plate in the presence of chemical reaction. International Journal of Applied Mathematics and Mechanics 4(1): 66- 74.
10. Saxena SS, Dubey GK (2011) MHD free convection heat and mass transfer flow of viscoelastic fluid embedded in a porous medium of variable permeability with radiation effect and heat source in slip flow regime. Advances in Applied Science Research 2(5): 115-129.
11. Ibrahim SM, Suneetha K (2016) Heat source and chemical effects on MHD convection flow embedded in a porous medium with Soret, viscous and Joules dissipation. Ain Shams Engineering Journal 7(2): 811-818.
12. Ibrahim SM, Suneetha K (2015) Chemical reaction and Soret effects on unsteady MHD flow of a viscoelastic fluid past an impulsively started infinite vertical plate with Heat source. International Journal of Mathematics and Computational Science 1(1): 5-14.
13. Noreen SA, SaleemM (2016) Soret and Dufour effects on the MHD peristaltic flow in a porous medium with thermal radiation and chemical reaction. Heat Transfer Research 47(1): 1-28.
14. Hayat T, Qayyum A, Alsaadi F, Awais M, Dobaie AM (2013) Thermal radiation effects in squeezing flow of a Jeffery fluid. The European Physical Journal Plus 128(8): 1-7.
15. Olajuwon BI (2011) Convection heat and mass transfer in a hydromagnetic flow of a second grade fluid in the presence of thermal radiation and thermal diffusion. International communications in heat and mass transfer 38(3): 377-382.
16. Rashidi MM, Ferdows M, Parsa AB, Abelman S (2014) MHD natural convection with convective surface boundary condition over a flat plate. Abstract and Applied Analysis, Hindawi Publishing Corporation, Egypt.
17. Rashidi MM, Kavyani N, Abelman S, Uddin MJ, Freidoonimehr N (2014) Double diffusive magnetohydrodynamic (MHD) mixed convective slip flow 9(10): e109404.
18. Stefan MJ (1874) Akad Wiss Wien Math-Natur. Klassa Abt 2: 69.
19. Reynolds O (1886) On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Proceedings of the Royal Society of London 40(242-245): 191-203.
20. Scott JR (1931) Theory and application of the parallel-plate plastometer. Trans Inst Rubber Ind 7: 169
21. Kuzma DC (1968) Fluid inertia effects in squeeze films. Applied Scientific Research 18(1): 15-20.
22. Ghori QK, Ahmed M, Siddiqui AM (2007) Application of homotopy perturbation method to squeezing flow of a Newtonian fluid. International Journal of Nonlinear Sciences and Numerical Simulation 8.2: 179-184.
23. Rashidi, Mehdi M, MajidSiddiqui A, Asadi M (2010) Application of homotopy analysis method to the unsteady squeezing flow of a second-grade fluid between circular plates. Mathematical Problems in Engineering, Hindawi Publishing Corporation, Egypt.
24. Qayyum A, Awais M, Alsaedi A, Hayat T (2012) Unsteady squeezing flow of Jeffery fluid between two parallel disks. Chinese Physics Letters 29(3): 034701.
25. Wang CY (1976) The squeezing of a fluid between two plates. Journal of Applied Mechanics 43(4): 579-583.
26. Rashidi MM, Shahmohamadi H, Dinarvand S (2009) Analytic approximate solutions for unsteady two-dimensional and axisymmetric squeezing flows between parallel plates. Mathematical Problems in Engineering, Hindawi Publishing Corporation, Egypt.
27. Siddiqui AM, Irum S, Ansari AR (2008) Unsteady squeezing flow of a viscous MHD fluid between parallel plates, a solution using the homotopy perturbation method. Mathematical Modelling and Analysis 13(4): 565-576.
28. Domairry G, Aziz A (2009) Approximate analysis of MHD squeeze flow between two parallel disks with suction or injection by homotopy perturbation method. Mathematical Problems in Engineering, Hindawi Publishing Corporation, Egypt.
29. Hayat T, Yousaf A, Mustafa M, Obaidat S (2012) MHD squeezing flow of second-grade fluid between two parallel disks. International Journal for Numerical Methods in Fluids 69(2): 399-410.
30. Khaled AR, Vafai K (2004) Hydromagnetic squeezed flow and heat transfer over a sensor surface. International Journal of Engineering Science 42(5): 509-519.
31. Mahmood M, Asghar S, Hossain MA (2007) Squeezed flow and heat transfer over a porous surface for viscous fluid. Heat and Mass Transfer 44(2): 165-173.
32. Duwairi HM, Tashtoush B, Damseh RA (2004) On heat transfer effects of a viscous fluid squeezed and extruded between two parallel plates. Heat and mass transfer 41(2): 112-117.
33. Mustafa M, Hayat T, Obaidat S (2012) On heat and mass transfer in the unsteady squeezing flow between parallel plates. Meccanica 47(7): 1581-1589.
34. Khan H, Islam S, Ali J, Ali Shah I (2012) Comparison of different analytic solutions to axisymmetric squeezing fluid flow between two infinite parallel plates with slip boundary conditions. Abstract and Applied Analysis, Hindawi Publishing Corporation, Egypt.
35. Ganji DD, Abbasi M, Rahimi J, Gholami M, Rahimipetroudi I (2014) On the MHD squeeze flow between two parallel disks with suction or injection via HAM and HPM. Frontiers of Mechanical Engineering 9(3): 270-280.
36. Shampine LF, Kierzenka J, Reichelt MW (2000) Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutorial notes 437-48.
37. Kuznetsov AV, Nield DA (2010) Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences 49(2): 243-247.
38. Khater AH, Temsah RS, Hassan MM (2008) A Chebyshev spectral collocation method for solving Burgers’-type equations, J Computational and Applied Mathematics 222(2): 333-350.
39. Sohail A, Uddin MJ, Rashidi MM (2015) Numerical study of free convective flow of a nanofluid over a chemically reactive porous flat vertical plate with a second-order slip model. Journal of Aerospace Engineering 29(2): 04015047.