Electrochemical Investigation of Electrolyte & Anodic Materials for Sodium Ion Batteries

Sodium-ion battery is a type of re-chargeable battery which uses sodium-ions as its charge carriers and is very similar to LIBTs in many ways. The measured reversible Sodium ion capacities of GO/Li&Na/GO based anodic materials are considerably improved compared to the conventional graphite-based anodic materials. Graphene oxide has displayed great behavior as suitable materials for anodic sodium ion batteries (LIBs) due to their unique properties. In this study GO sheet has been localized inside the graphene as an option to enhance electrochemical ratio. Moreover, the structure of GO/Li&Na/GO can be to improve the capacities and electrical transport in GO sheets-based LIBs. Therefore, the modification of GO sheet and design of GO/Li&Na/GO structure provide strategies for improving the performance of GO-based anodes. GO/Li&Na/GO could also be assembled into freestanding electrodes without any binder or current collector, which will lead to increased energies density for overall batteries designing. In addition, the relationship among electrical and ionic conduction for three cathode materials including LiCoO₂, LiMn₂O₄, LiFePO₄ have been discussed towards phase changing in sodium anodes and how it relates to diffusivity and conductivity and the key conduction issues with some organic liquid and ionic liquid electrolytes.

Keywords: Graphene oxide (GO); Anodic materials; Lithium ion batteries

Na ions are 33% larger in diameter and 2.1 times heavier within lower gravimetric capacities than Li-ion batteries [1]. In addition Na metals are more active than Li with the standard electrode potentials which is ~0.3V higher than Li.

Sony realized the commercialization of xC6/Li _1-x CoO₂ cells [1] in 1991. Lithium ion batteries (LIBs) are representative energies storage devices based on electrochemical energies, widely used in small grid storage systems. Within discovery of highly reversible, low-voltage Li-intercalation carbonaceous materials, the favorable electrochemical performance of LIBs regarding energies and power densities, as well as the progress in cell designing and manufacturing, have made LIBs greatly successful for mobile electronics.

However; the Na+ ion has a larger radius than the Li+ ion, which makes many of the superior LIB electrode materials unsuitable for NIBs, concerns regarding the future availability of lithium resources are raising. Sodium ion batteries [2] (NIBs) have been drawing increasing attention [3] because Na is an earth abundant element and shares common properties with Li [2-4]. In particular, graphite [5] is a widely used anode material for the present commercial LIBs, while it has been reported to have a very low capacity of when used as an anode for NIBs [5-7].

Both disordered carbon and Nano-flakes [8] (CNFs) exhibits high Na intercalation [9] capacity and emerges as a leading candidate for NIB applications. In this study we tried to build a model for GO and investigate its mechanism for Na intercalation into the layered domains. However, the mechanism of Na+ ion insertion into disturbed carbon is still controversial [10]. It is believed that a larger interlayer distances [11] of those carbons, which are larger than the interlayer distance of graphite, helps Na+ ion intercalation. As a result, defects may enhance Na intercalation by the strong bonding energy to overcome the van der Waals energies between graphene sheets [12]. By this work we evaluate the reliability of various semi-empirical corrections and vdW exchange correlation functional to determine the optimal method for the present study. Graphite is currently the most common material used for the anodes of commercial batteries because of its capability for reversible lithium intercalation in the layered crystals, which represents the maximum theoretical Sodium storage capacity [13].

NIBs typically consist of a positive electrode, a negative electrode and a conducting electrolyte where store electrical energy in the two electrodes in the form of Na-intercalation compounds [11]. Electrodes, separator, and electrolyte are the main components of the NIB where the anode plays an essential role in the performance of these kind devices [12,13].

The structure and properties of graphite oxide depend on particular synthesis method and degree of oxidation. It typically preserves the layer structure of the parent graphite, but the layers are buckled and the interlayer spacing is about two times larger (~0.7nm) than that of graphite that provides suitable environment for sodium diffusion in a NIBs [11] XRD, FTIR, Raman, XPS, AFM, TEM, etc. are some common techniques to characterize GO samples [13] . Since the distribution of oxygen functionalities on GO sheets is poly-disperse, fractionation method using emulsion stabilization can be used to characterize and separate GO sheets on the basis of oxidation [14]. During charging of the NIBs, Sodium ions released from the cathode move through the electrolyte and are inserted into the anode. Upon discharging, Sodium ions are extracted from the anode and move back to the cathode. Although the electrolyte establishes high ionic conductivity between two electrodes, the electrolytes are not responsible for the conduction of free electrons and so the electrons complete the half reaction will move through an extra external wire [14,15]. There are a number of reviews on anode materials [15-20] and many of them focus on both carbon and inorganic materials [18].

Discharging and charging of Li-ions in graphitized [19] carbon is well established and documented up to now [21-24]. It has also been shown how repulsive forces [20] in a mixed stage can result in a pure stage during intercalation [22]. Although attempts have been made to find suitable replacements [23], currently only carbonaceous materials are used in commercial anodes [25]. Carbonaceous materials' properties largely depend on the starting materials such as carbon precursor and heat treatment [26].

In this study, charging and discharging of Na-ions has investigated24 in Graphite oxide (GO) with the positive electrode reaction [25] as: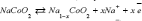 and the negative electrode reaction as: while the whole reaction is: 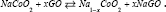.It has been suggested that Sodium atoms are stored [26] via two mechanisms: intercalation and alloying [27]. GO similar Graphite is known as a small band gap semi-metal due to its unique conduction behavior under the influence [27] of electrical fields [28,29]. Interlayer forces [30] are small (van der Waals force), and the distance between GO layers [31] is large allowing Na-ions to easily diffuse between GO sheets [32]. Electrical conductivity of the Na-GO increases, due to the electron donor nature of the Na [33]. Based on our previous works we have used various methods to simulate the NIBs and calculated the NMR, solvent effect [24], voltages, charges and physical properties of our model [32-53].

Na⁺ diffusion

Diffusion of Na⁺ in the cells determine the key performance metrics of Na-ion batteries cells, with the charge and discharge rates, practical capacities and cycling stabilities. The governing equations describing the diffusion [54] process are known as Fick's law as: 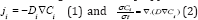where "ji" is ionic flux, molcm^-2s^-1, Di is diffusivity of solute (i =1, 2), cm²s^-1 and Ci are concentration of species i, (molcm³) [54]. The proportionalities [71] factor D is the diffusivities or diffusion coefficient as 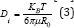[54,55].

In condensed materials both liquids and solids, diffusion is governed by random jumps of atoms or ions, leading to position exchange with their neighbors. The kinetics of these processes is temperature dependent and follows an Arrhenius type relationship 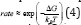[56]. In liquids, the temperature dependence of the diffusion [55] is much less than in solids.

Cathode materials

In an extended approach they can be classified as

a. Layered compounds NaMO₂ (M = Co,Ni,Mn)

b. Spinel compounds NaM₂O₄ (M = Mn, etc.)

c. Olivine compounds NaMPO₄ (M = Fe, Mn, Ni, Co, etc.)

Figure 1: The conduction phenomena in cathode particles during charge.

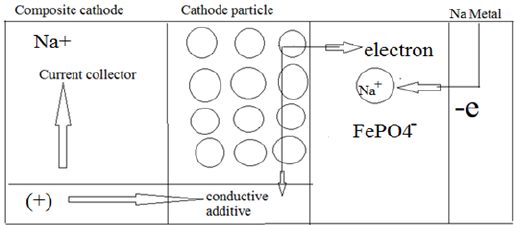
When a Na-ion diffuses [57] out of the cathode (ionic ion is oxidized to Fe³⁺. The reaction in cathode can be written as: conduction) during the charge cycle the valence state of the (Figure 1) transition [58] metal ion changes (electronic conduction); the Fe²⁺ ion is oxidized to Fe³⁺. The reaction in cathode can be written as: (Figure 1)

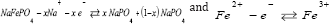
Thus, it is important that electrical and ionic conductivities be optimized in cathode materials, since either of these values can dictate the overall cell properties including capacity and cycle life [59,60].

Anode materials

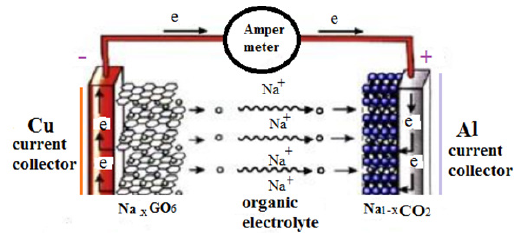
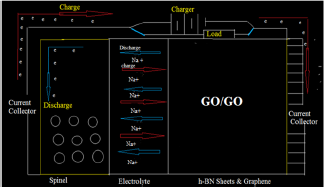
In the case of anode, Natrium is found to be the suitable electropositive particles with large reversible capacities. However, due to safety considerations [61], metallic Na has been substituted by various carbonaceous materials such as GO. GO-sodium anode has much lower gravimetric and volumetric energies density than pure sodium which leads toward the development of 3d transition metal oxides [61]. (M_xO_y, M = Fe, Co, Ni, Mn, Cu) [61,62]. The diffusivity [60] of Li-ions in graphite is complicated by the constant phase change in the Na-GO intercalation compound, which can introduce disorder [61] into the originally ordered structure. During discharge, Na+ ions are extracted from the layered graphite, they pass through the electrolyte and intercalate between the NaCoO₂ layers (Figure 2).

Figure 2: A typical commercial sodium-ion battery, the reversible process is: mC+Nacoo₂Na_nc_m+Na_1-nCoO₂.

Electrolyte material

Interpretation of in situ characterization experiments is challenging often due to a lack of viable theories concerning cathodes, anodes, and novel electrolytes .The ideal electrolyte for Na/Li-ion batteries has not yet been known; although organic electrolytes are used due to their suitable ionic conductivities and good ranges of practical operating temperature, there are many reasons for developing alternatives. While several material systems have been tested as replacements, most do not display a sufficient ionic conductivity to be utilized in Li-ion batteries; the room temperatures conductivities of are needed for an electrolyte to function well in consumer battery systems.

Carbon-sodium anodes have much lower gravimetric and volumetric energy densities than pure sodium which lead towards the development of interstitial-free 3d transition metal oxides.

Electron density profiles

The electron densities have been defined [63] as (5). Where is occupation [64] number of orbital (i), is orbital wave function, x is basis function and C is coefficient matrix, the element of i_it, row j_thcolumn corresponds to the expansion coefficient of orbital j respect to basis function [65,66] i. Atomic unit for electron density can be explicitly written as e/Bohr³.

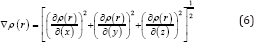
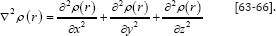
Electron localization function (ELF)

Becke AD & Edgecombe KE [67] noted that spherically averaged like-spin conditional pair probability [66,67] has direct correlation with the Fermi hole and then suggested electron localization function (ELF).

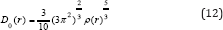
Savin et al. [68] have reinterpreted ELF in the view of kinetic energy, which makes ELF also meaningful [68] for Kohn W & Sham LJ [69] DFT wave-function or even post-HF wave-function [68]. They indicated that D(r) reveals [69] the excess kinetic energy density caused by Pauli repulsion, while D0(r) can be considered as Thomas-Fermi kinetic energy density [68,69]. Localized orbital locator [69] (LOL) is another function for locating high localization regions68 likewise ELF, defined by Schmider and Becke in the paper [69,70].

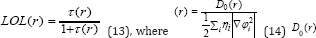
for spin-polarized system and close-shell system are defined in the same way as in ELF [71-77].

Computational details

Calculations were performed using both Gaussian and GAMESS-US packages [78]. In this study, we have mainly focused on getting the optimized results for each tube from DFT methods including the m06 and m06-L. The m062x, m06-L, and m06-HF are a novel Meta hybrid DFT functional with a good correspondence [78] in non-bonded calculations and are useful for calculating the energies of the distance between two plates of GO sheets [79]. Pm6, Extended-Huckel and Pm3MM including pseudo=lanl2 calculations using Gaussian program have done for the non-bonded interaction between two tubs [79].

M06 and m06-L (DFT) functional is based on an iterative solution of the Kohn-Sham [78,79] equation [80] of the density functional theory in a plane-wave [80] set with the projector- augmented wave pseudo-potentials [79-80]. The Perdew-Burke- Ernzerhof (PBE) [81] exchange-correlation (XC) functional of the generalized gradient approximation (GGA) is adopted. The optimizations of the lattice constants and the atomic coordinates are made by the minimization of the total energy [79-81]. We employed density functional theory with the van der Waals density functional to model the exchange-correlation energies of h-BN sheets [82]. The double ζ-basis set with polarization orbitals (DZP) were used for x sodium over the GO sheets [81].

For non-covalent interactions, the B3LYP method is unable to describe [83] van der Waals capacitor systems by medium-range interactions such as the interactions of two cylinders. We further calculated the interaction energy between x sodium and GO sheets. The interaction energy was calculated via the Mp6 method in all items according to where the " is the stability energy of system [83].

The charge transfer and electrostatic potential-derived charge were also calculated using the Merz-Kollman PA et al. [84], Chirlian LE et al. [85], or Breneman GM et al. [86].

Table 1: Various Densities, Spin, Lagrangian, K(r), V(r) , ELF and LOL for 8 Na/Na+ insertion.

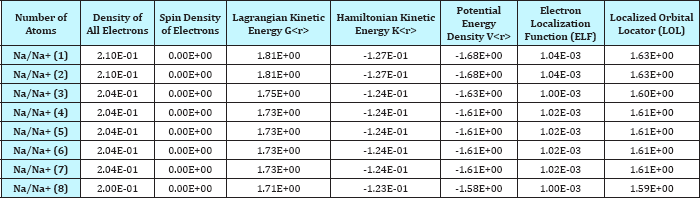
We have calculated the gradient norm and the Laplacian of electron density via Eqs (7,8) for the Sodium diffused in the GO system respectively and the data are listed in Table 1. For calculation the electron spin density from the difference between alpha and beta density, we have used ρ^S (r) = ρ^α (r)-ρ^β (r) then the spin polarization parameter function will be returned instead of spin density

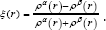
The data of Density, energy, Electron localization function (ELF), Localized orbital locator (LOL) and Local Entropy, Gap energy, charges from ESP, electrostatic potential , Ionization energy, the Charges of two graphene electrodes and the stability energy of GO sheets have been listed in (Table 1 & 2) and these data have been plotted in seven figures (Figure 1-7)

The absolute value of ξ going from zero to unity corresponds to the local region going from un-polarized case to completely polarized case Table1.

The kinetic energy density, Lagrangian kinetic energy density, and the electrostatic potential from nuclear/atomic charges can be calculated as eqs. (9), (10) and: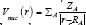 where RA and ZA denote position vector and nuclear charge of atom A, respectively and are listed in Table 1& 2. The larger the electron localization is in a region, the more likely the electron motion is confined within it. If electrons are completely localized, then they can be distinguished from the ones outside. Bader found that the regions which have large electron localization must have large magnitudes of Fermi hole integration. However, the Fermi hole is a six-dimension function and thus difficult to be studied visually.

Figure 3: ELF, LOL, K(r) and G(r) for 16 Na+ insertion between two layers of GO sheets.

Table 2: Various Densities, Spin, Lagrangian, K(r), V(r), ELF, LOL and ESP for 12 Na+/Na insertion.

LOL has similar expression compared to ELF. Actually, the chemically significant regions that highlighted by LOL and ELF are generally qualitative comparable, while Jacobsen pointed out that LOL conveys more decisive and clearer picture than ELF, Obviously LOL can be interpreted in kinetic energy way as for ELF; however LOL can also be interpreted in view of localized orbital. Small (large) LOL value usually appears in boundary (inner) region of localized orbitals because the gradient of orbital wave-function is large (small) in this area. The value range of LOL is identical to ELF, namely [0, 1].

If pseudo potential is used, then Z is the number of explicitly expressed electrons. Z can be stand for the atomic charges recorded in the file (the fourth column), at this time V_nu is useful for analyzing the difference between exact electrostatic potential and the electrostatic potential reproduced by atomic charges. Notice that at nuclear positions, this function will be infinite and may cause some numerical problems in program; hence at these cases this function always returns 1000 instead of infinity.

Since D0(r) from eqs 11-13 is introduced into ELF as reference, what the ELF reveals is actually a relative localization. ELF is within the range of [0, 1]. A large ELF value means that electrons are greatly localized, indicating that there is a covalent bond, a lone pair or inner shells of the atom involved. ELF has been widely used for a wide variety of systems, such as organic and inorganic small molecules, atomic crystals, coordination compounds, clusters, and for different problems, such as the revealing atomic shell structure, classification of chemical bonding, verification of charge-shift bond, studying aromaticity.

Figure 4: Density and LOL for Na+/Na insetion.

Figure 5: Sodium and Ion sodium diffusion between two GO layers.

Figure 6: Operating Na-ion battery.

In which the actual kinetic energy term in D(r) from eqs. 1516 is replaced by Kirzhnits type second-order gradient expansion, that is so that ELF is totally independent from wave-function, and then can be used to analyze electron density from X-ray diffraction data. Of course Tsirelson's ELF can also be used to analyze electron density from quantum chemistry calculation, but is not as good as the ELF defined by Becke owing to the approximation introduced in kinetic energy term; however, qualitative conclusions can still be recovered in general.

The data of Density, energy, Electron localization function (ELF), Localized orbital locator (LOL) and Local Entropy, Gap energy, charges from ESP, electrostatic potential, Ionization energy, the Charges of two graphene electrodes and the stability energy of GO sheets have been listed in (Table 1 & 2) .The absolute value of ξ going from zero to unity corresponds to the local region going from un-polarized case to completely polarized case Table 1. ELF data in Table 2 in view point of kinetic energy makes a meaningful of Kohn-Sham "DFT" wave-function or even post-HF wave-function. Localized orbital locator (LOL) in Table 3 is another function for locating high localization regions likewise ELF, defined by Schmider & Becke [71] in the paper (Tables 1-3).

Figure 7: Shaded surface map with projection for insertion 10 Na+/Na.

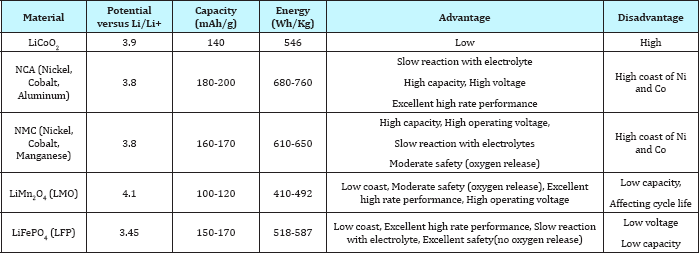
Table 3: Characteristics of commercial Li-ion battery cathode materials see reference [1].

In conclusion, our calculations have been designed to study the Na adsorption on graphene oxide with two layers of GO. Our results exhibit that adsorption in GO is much stronger than pristine graphene. Additionally, it has been found the structure of GO can be to improve the electrical transport in NIBs. Therefore, the modification and design of GO structure provide strategies for improving the performance of GO-based anodes. With the increase in defect density by GO sheets, maximum capacities obtained are much higher than that of graphite.

1. Yang ZG, Zhang JL, Kintner-Meyer MCW, Lu XC, Choi DW, et al. (2011) Electrochemical energy storage for green grid. Chem Rev 111: 35773613.
2. Barpanda P, Oyama G, Nishimura SI, Chung SC, Yamada A (2014) Intermediate honeycomb ordering to trigger oxygen redox chemistry in layered battery electrode. Nat Commun 5: 4358.
3. Slater MD, Kim D, Lee E, Johnson CS (2013) High-capacity antimony sulphide nanoparticle-decorated graphene composite as anode for sodium-ion batteries. Adv Funct Mater 23: 947.
4. Yabuuchi N, Kubota K, Dahbi M, Komaba S (2014) Research development on sodium-ion batteries. Chem Rev 114(23): 11636-11682.
5. Ge P, Fouletier M (1988) Electrochemical intercalation of sodium in graphite. Solid State Ionics 28-30(2): 1172-1175.
6. Stevens D, Dahn J (2001) The mechanisms of lithium and sodium insertion in carbon materials . J Electrochem Soc 148(8): A803-A811.
7. Mizutani Y, Abe T, Inaba M, Ogumi Z (2001) Synth Met 125:153.
8. Stevens DA, Dahn JR (2000) High capacity anode materials for rechargeable sodium-ion batteries. J Electrochem Soc 147(4): 12711273.
9. Schniepp HC, Li JL, McAllister MJ, Sai H, Herrera-Alonso M, et al. (2006) Functionalized single graphene sheets derived from splitting graphite oxide. The Journal of Physical Chemistry B 110(17): 8535-8539.
10. Pandey D, Reifenberger R, Piner R (2008) Scanning probe microscopy study of exfoliated oxidized graphene sheets. Surface Science 602(9): 1607-1613.
11. Talyzin AV, Szabô TS, DéKaNy I, Langenhorst F, Sokolov PS, et al. (2009) Nanocarbons by high-temperature decomposition of graphite oxide at various pressures. The Journal of Physical Chemistry C 113(26): 1127911284.
12. Daniela MC, Dmitry VK, Jacob MB, Alexander S, Zhengzong S, et al. (2010) Improved synthesis of graphene oxide. ACS Nano 4(8): 4806-4814.
13. Kumar, Harish V, Woltornist, Steven J, Adamson, et al. (2015) Fractionation and characterization of graphene oxide by oxidation extent through emulsion stabilization. Carbon 98: 491-495.
14. Suzuki T, Hasegawa T, Mukai SR, Tamon H (2003) A theoretical study on storage states of Li ions in carbon anodes of Li ion batteries using molecular orbital calculations. Carbon 41(10): 1933-1939.
15. Hasegawa T, Suzuki T, Mukai SR, Tamon H (2003) Semi-empirical molecular orbital calculations on the Li ion storage states in heteroatom- substituted carbon materials. Carbon 42(11): 2195-2200.
16. Noel M, Suryanarayanan V (2002) Role of carbon host lattices in Li- ion intercalation/de-intercalation processes. Journal of Power Sources 111(2): 193-209.
17. Tirado JL (2003) Inorganic materials for the negative electrode of lithium-ion batteries: state-of-the-art and future prospects. Materials Science and Engineering R 40(3): 103-136.
18. Fu LJ, Liu H, Li C, Wu YP, Rahm E, et al. (2006) Surface modifications of electrode materials for lithium ion batteries. Solid State Sciences 8(2): 113-128.
19. Frackowiak E, Béguin F (2002) Electrochemical storage of energy in carbon nanotubes and nanostructured carbons. Carbon 40(10): 17751787.
20. Whittingham MS, Jacobson AJ (1982) Intercalation Chemistry, Academic Press, USA.
21. Safran SA, Hamann DR (1979) Long-range elastic interactions and staging in graphite intercalation compounds. Physical Review Letters 42(21): 1410-1413.
22. Levi MD, Aurbach D, Maier J (2008) Electrochemically driven first-order phase transitions caused by elastic responses of ion-insertion electrodes under external kinetic control. Journal of Electroanalytical Chemistry 624(1-2): 251-261.
23. Zabel H, Solin SA (Eds.) (1990) Graphite Intercalation Compound I, Springer-Verlag, Germany
24. Wu YP, Rahm E, Holze R (2003) Carbon anode materials for lithium ion batteries. Journal of Power Sources 114(2): 228-236.
25. Lee JK, An KW, Ju JB, Cho BW, Cho WI, et al. (2001) Electrochemical properties of PAN-based carbon fibers as anodes for rechargeable lithium ion batteries. Carbon 39(9): 1299-1305.
26. De las Casas C, Li WZ (2012) A review of application of carbon nanotubes for lithium ion battery anode material. J Power Sources 208: 74-85.
27. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, et al. (2004) Electric field effect in atomically thin carbon films. Science 306(5696): 666-669.
28. Partoens B, Peeters FM (2006) From graphene to graphite: Electronic structure around the K point. Physical Review B 74: 075404.
29. Monajjemi M, Lee VS, Khaleghian M, Honarparvar B, Mollaamin BF (2010) Theoretical description of electromagnetic nonbonded interactions of radical, cationic, and anionic NH₂BHNBHNH₂ inside of the B₁₈N₁₈ nanoring. J Phys Chem C 114(36): 15315-15330.
30. Monajjemi M (2012) Quantum investigation of non-bonded interaction between the B₁₅N₁₅ ring and BH₂NBH₂ (radical, cation, anion) systems: a nano molecularmotor. Struct Chem 23(2): 551-580.
31. Monajjemi M, Baei MT, Mollaamin F (2008) Quantum mechanics study of hydrogen chemisorptions on nanocluster vanadium surface. Russian Journal of Inorganic Chemistry 53(9): 1430-1437.
32. Monajjemi M, Boggs JE (2013) A New Generation of B_nN_n Rings as a Supplement to Boron Nitride Tubes and Cages. J Phys Chem A 117(7): 1670-1684.
33. Monajjemi M, Khaleghian M (2011) EPR study of electronic structure of [CoF₆]^3-and B₁₈N₁₈ nano ring field effects on octahedral complex. Journal of Cluster Science 22(4): 673-692.
34. Mollaamin F, Varmaghani Z, Monajjemi M (2011) Dielectric effect on thermodynamic properties in vinblastine by DFT/Onsager modelling. Physics and Chemistry of Liquids 49(3): 318-336.
35. Monajjemi M (2013) Non bonded interaction between B_nN_n (stator) and (rotor) systems: A quantum rotation in IR region. Chemical Physics 425: 29-45.
36. Monajjemi M, Wayne, Robert Boggs JE (2014) NMR contour maps as a new parameter of carboxyl's OH groups in amino acids recognition: A reason of tRNA-amino acid conjugation. Chemical Physics 433: 1-11.
37. Monajjemi M, Falahati M, Mollaamin F (2013) Computational investigation on alcohol nanosensors in combination with carbon nanotube: a Monte Carlo and ab initio simulation. Ionics 19(1): 155-164.
38. Monajjemi M, Mollaamin F (2012) Molecular modeling study of Drug- DNA combined to single walled carbon nanotube. Journal of Cluster Science 23(2): 259-272.
39. Tahan A, Monajjemi M (2011) Solvent dielectric effect and side chain mutation on the structural stability of Burkholderia cepacia lipase active site: a quantum mechanical/molecular mechanics study. Acta Biotheor 59(3-4): 291-312.
40. Mollaamin F, Monajjemi M (2012) DFT outlook of solvent effect on function of nano bioorganic drugs. Physics and Chemistry of Liquids 50(5): 596-604.
41. Monajjemi M, Khosravi M, Honarparvar B, Mollaamin F (2011) Substituent and solvent effects on the structural bioactivity and anticancer characteristic of catechin as a bioactive constituent of green tea. International Journal of Quantum Chemistry 111(12): 2771-2777.
42. Monajjemi M, Baheri H, Mollaamin F (2011) A percolation model for carbon nanotube-polymer composites using the Mandelbrot-Given curve. Journal of Structural Chemistry 52(1): 54-59.
43. Monajjemi M (2015) on-covalent attraction of B₂N^(-,0) and repulsion of B₂N^(t) in the B_nN_n ring: a quantum rotatory due to an external field. Theor Chem Acc 134: 77.
44. Monajjemi M (2014) Journal of Molecular Modeling 20: 2507.
45. Monajjemi M, Khaleghian M, Mollaamin F (2010) Theoretical study of the intermolecular potential energy and second virial coefficient in the mixtures of CH₄ and Kr gases: a comparison with experimental data. Molecular Simulation 36(11): 865-870.
46. Monajjemi M (2015) Cell membrane causes the lipid bilayers to behave as variable capacitors: A resonance with self-induction of helical proteins. Biophysical Chemistry 207: 114-127.
47. Monajjemi M, Sarasia EM, Afsharnezhad S, Honarparvar B, Mollaamin F(2011) Theoretical study of solvent effect on NMR shielding tensors of luciferin derivatives. Physics and Chemistry of Liquids 49(5): 561-571.
48. Jalilian H, Monajjemi M (2015) Capacitor simulation including of X-doped graphene (X = Li, Be, B) as two electrodes and (h-BN)_m (m = 1-4) as the insulator. Japanese Journal of Applied Physics 54(8): 085101.
49. Mahdavian L, Monajjemi M (2010) Alcohol sensors based on SWNT as chemical sensors: monte carlo and langevin dynamics simulation. Microelectronics Journal 41(2-3): 142-149
50. Tahan A, Mollaamin F, Monajjemi M (2009) Thermochemistry and NBO analysis of peptide bond: Investigation of basis sets and binding energy. Russian Journal of Physical Chemistry A 83(4): 587-597.
51. Monajjemi M, Bagheri S, Moosavi MS, Moradiyeh N, Zakeri M, et al. (2015) Symmetry breaking of B₂N (-, 0, +): An aspect of the electric potential and atomic charges. Molecules 20(12): 21636-21657.
52. Monajjemi M (2017) Liquid-phase exfoliation (LPE) of graphite towards graphene: An ab initio study. Journal of Molecular Liquids 230: 461-472.
53. Monajjemi M (2017) Graphene/(h-BN) n/X-doped graphene as anode material in lithium ion batteries (X=Li, Be, B and N). Maced J Chem Chem Eng 36(1): 101-118.
54. Wilkinson DS (2000) Mass Transport in Solid and Fluids, Cambridge University Press, India.
55. Mehrer H (2007) Diffusion in Solids, Springer, USA, pp. 27-36.
56. Porter DA, Easterling KE (1992) Phase transformations in metals and alloys. (2^nd edn), Chapman & Hall, UK, pp: 1-109.
57. Petrucci RH, Harwood WS (1997) General Chemistry. (7^th edn), Prentice- Hall, USA, pp. 315-343.
58. Dehmelt H (1998) A single atomic particle forever floating at rest in free space: new value for electron radius. Physica Scripta 22: 102-110.
59. Wang C, Hong J (2007) Ionic/electronic conducting characteristics of LiFePO₄ cathode materials: The Determining factors for high rate performance. Electrochemical and Solid-State Letters 10(3): A65-A69.
60. Majid Monajjemi (2017) Graphene/(h-BN) n/X-doped graphene as anode material in lithium ion batteries (X=Li, Be, B and N). Maced J Chem Chem Eng 36(1): 101-118.
61. Poizot P, Laruelle S, Grugeon S, Dupont L, Tarascon LJM (2000) Nature 407(6803): 496-499.
62. Churikov AV, Gridina NA, Churikova NV, Igor V, Christopher S, et al. (2006) New Carbon based materials for electrochemical energy storage systems: Batteries, Supercapacitors and Fuel Cells, Springer, pp. 269276.
63. Lu T, Chen F (2011) Calculation of molecular orbital composition. Acta Chim Sinica 69(20): 2393-2406.
64. Lu T, Chen F (2012) Quantitative analysis of molecular surface based on improved marching tetrahedra algorithm. J Mol Graph Model 38: 314-323.
65. Lu T, Chen F (2012) Multiwfn: a multifunctional wave-function analyzer. J Comp Chem 33(5): 580-592.
66. Bader RFW (1990) Atoms in Molecule: A quantum Theory, Oxford Univ press, Oxford, UK.
67. Becke AD, Edgecombe KE (1990) A simple measure of electron localization in atomic and molecular systems. J Chem Phys 92(9): 5397.
68. Savin A (1992) Electron localization in solid-state structures of the elements: the diamond structure. Angew Chem Int Ed Engl 31(2): 187188.
69. Kohn W, Sham LJ (1965) Self-consistent equations including exchange and correlation effects. Phys Rev 140 : A1133-A1138.
70. Tsirelson VG, Yu A, Abramov (2002) Determination of the electron localization function from electron density. Chem Phys Lett 351(1-2): 142-148.
71. Schmider HL, Becke AD (2000) Chemical content of the kinetic energy density. J Mol Struct Theochem 527(1-3): 51-61.
72. Jacobsen H (2008) Localized-orbital locator (LOL) profiles of chemical bonding. Can J Chem 86(7): 695-702.
73. Aslangul C, Constanciel R, Daudel R, Kottis P (1972) Aspects of the localizability of electrons in atoms and molecules: loge theory and related methods. Adv Quantum Chem 6: 93-141.
74. Parr RG, Ayers PW, Nalewajski RF (2005) What is an atom in a molecule?. J Phys Chem A 109(17): 3957-3959.
75. Noorizadeh S, Shakerzadeh E (2010) Shannon entropy as a new measure of aromaticity, Shannon aromaticity. Phys Chem Chem Phys 12(18): 4742.
76. Murray JS, Politzer P (1994) Statistically-based interaction indices derived from molecular surface electrostatic potentials: a general interaction properties function (GIPF). J Mol Struct (Theochem) 307: 55-64.
77. Murray JS (2011) The electrostatic potential: an overview. Comput Mol Sci 1(2): 153-163.
78. Politzer P, Murray JS (2002) The fundamental nature and role of the electrostatic potential in atoms and molecules. Theor Chem Acc 108(3): 134-142.
79. Schmidt MW, Baldridge KK, Boatz JA, Elbert ST, Gordon MS, et al. (2004) General atomic and molecular electronic structure system. J Comput Chem 14(11): 1347-1363.
80. Yan Zhao, Donald GT (2008) The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functional. Theor Chem Account 120(1-3): 215-241.
81. Perdew JP, Burke K, Ernzerhof (1996) Generalized Gradient Approximation Made Simple. Phys Rev Lett 77: 3865-3868.
82. Klein DL, Roth R, Lim AKL, Alivisatos AP, McEuen PL (1977) A singleelectron transistor made from a cadmium selenide nanocrystal. Nature 389: 699-701.
83. Yan Zhao, Donald GT (2008) Density functionals with broad applicability in chemistry. Accounts of Chemical Research 41(2): 157-167.
84. Besler BH, Merz KM, Kollman PA (1990) Atomic charges derived from semiempirical methods. J Comp Chem 11(4): 431-439.
85. Chirlian LE, Francl MM (1987) Atomic charges derived from electrostatic potentials: A detailed study. J Comp Chem 8(6): 894-905.
86. Breneman GM, Wiberg KB (1990) Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J Comp Chem 11(3): 361-373.