- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Polymer Science: Peer Review Journal
The Influence of Unidirectionally or Randomly Oriented CNTs on the Elastic Properties of Reinforced Composites
Kazakov IA* and Krasnovskii AN*
Department of Composite Materials, Moscow State Technological University STANKIN, Russia
*Corresponding author: Kazakov IA and Krasnovskii AN, Department of Composite Materials, Moscow State Technological University STANKIN, 127055 Moscow, Russia
Submission: September 23, 2020;Published: November 30, 2021
ISSN: 2770-6613 Volume2 Issue4
Abstract
The paper studies the influence of CNTs on the elastic properties of unidirectionally aligned composites. The nano-inclusions, whose properties could be characterized by three parameters (length, diameter, Young’s elastic modulus), are assumed to be ellipsoidal and oriented along a macro-filler (for example, glass fibers). The elastic properties of two systems: Matrix+CNT+Glass fibers and Matrix+Glass fibers were determined and compared.
Keywords: Nano-inclusions; CNTs; Eshelby; Mori-tanaka; Nidltrusion; Pultrusion
Introduction
In recent years, in connection with the development of technologies for the production of nano-modified composites (in particular, pultrusion and nidltrusion technologies [1,2]), there is a need to assess the effect of CNT on the properties of composites with unidirectionally aligned fibers. By a proper combination of fibers, matrix and aligned CNTs as additives a wide range of elastic properties can be achieved. In our previous work [3], an effective tool for determining the elastic properties of nano-reinforced composites based on the Eshelby-Mori- Tanaka’s method [4-7] was proposed. The model with an ellipsoidal inclusion in an infinite medium for an epoxy matrix reinforced with randomly oriented nanotubes allows obtaining a set of two independent elastic properties of the isotropic Matrix/CNT system. In the case of unidirectional CNTs, we obtain a set of five independent elastic constants of the transversely isotropic Matrix/CNT system. However, in the case of nanotubes oriented along a macro-filler (for example, glass fibers) the elastic properties of the Matrix+ CNT/Fiberglass system (we denote such a system as “compIICNT” for brevity) cannot be applied using the model with an ellipsoidal inclusion. This is due to the fact that the matrix with CNTs has not isotropic, but transversely isotropic properties. The goal of the current research is to explore Eshelby- Mori-Tanaka’ model for predicting effective elastic properties of unidirectionally aligned composites with unidirectionally or randomly oriented CNTs.
Theoretical Modeling
For a qualitative comparison of the two systems (compXCNT and compIICNT), we use the equations for engineering constants [8]. The longitudinal Young’s modulus E1 (1):
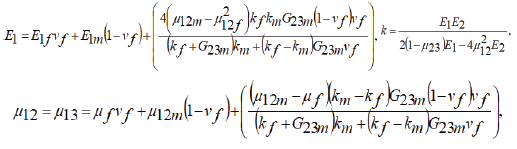
where indices f, m refers to fibers and matrix, respectively, ν– the mass fraction, μ–Poisson’s ratio, k–the bulk modulus at plane strain, kT–the effective composite modulus, in-plane shear modulus G12, G13 (2):
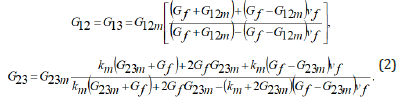
The transverse Young’s modulus E2 (3):
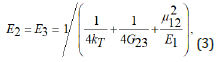
Having these constants defined, all the elastic properties of the composite will be fully determined. It should be noted that the properties of the matrix reinforced by CNTs are calculated using Eshelby-Mori-Tanaka’s model described in [3].
Results and Discussion
We assess the influence of the nanotube reinforcement on the
macroscopic properties of the unidirectionally aligned polymer
composites. To make the effect of aspect ratio α=L/D and CNTs mass
fraction WCNT (in percentage) more apparent, independent elastic
constants were presented in the form of relations to the initial
properties (WCNT=0) and plotted as a function of α and WCNT.
This made it possible to understand how the addition of filler in the
form of CNT affects the properties of the composite. It should be
mentioned that WCNT is the mass fraction relatively to the volume
occupied by resin+CNTs system. For example, WCNT=100% means
that composite consists of 60% fiberglass and 40% CNTs (no
resin). As was mentioned above, fiberglass volume fraction vf=60%
assumed constants for all numerical experiments.
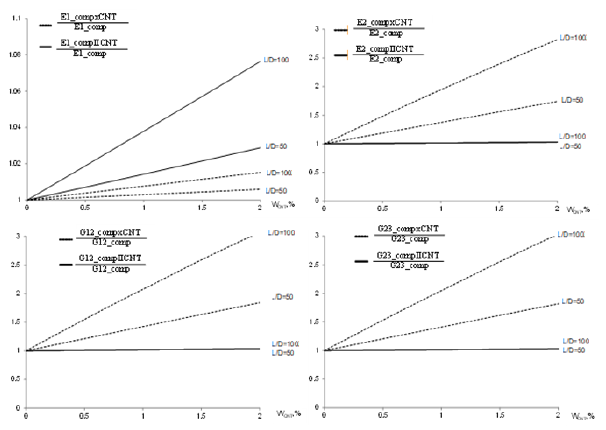
As shown in Figure 1, we employed values of CNTs up to
2% to avoid intersections between different fibers (i.e., the
interphase regions). Figure 1 shows that in unidirectional polymer
composites with oriented along a macro-filler nanotube an
overall reinforcement effect is noticed increasing by decreasing
the diameter of the embedded nanotubes. The addition of CNT
in fiberglass/epoxy composites of up to 2% by weight results
in insignificant increasing the mechanical properties in main
direction (E1), since the fibers are the main component carrying
the load. For the modified by CNTs composite of the variations of
three independent relative elastic constants, the transverse Young’s
modulus E2, in-plane shear modulus G12, and out-plane shear
modulus G23 appear to significantly increase with increasing CNT’s
concentration and length/diameter ratio for randomly oriented
CNTs in the composite.
Figure 1: Normalized elastic properties E1, E2, G12, G23 for polymer composites with unidirectional fiberglass filler (vf=0.6) and oriented along a macro-filler CNTs.
Conclusion
The modification of composites is critically important to improve its strength and mechanical properties, and to widespread its practical applications in many areas of outdoor, construction buildings, engineering, and technology sectors. As was shown in this article, dispersed CNTs around the unidirectional fibers was found be very effective for reinforcing composites. The mechanical properties of two systems: Matrix+CNT+Fiberglass and Matrix+Fiberglass were determined and compared using of Eshelby’s and Mori-Tanaka’s theories of inclusions. However, the curing and aging of epoxy resins are complex phenomena and the composite can show the agglomeration of CNTs, which can in turn have a negative effect on the mechanical properties of the composite, which is not taken into account in the model. An estimation of the effect of CNT on the properties of unidirectional fiberglass, depending on the concentration of CNT and the geometric ratio α=L/D, was made.
References
- Sun SP, Wei M, Olson JR, Shaw MT (2015) A modified pultrusion process for preparing composites reinforced with continuous fibers and aligned hydroxyapatite nanoneedles. Polymer Composites 36(5): 931-938.
- Kazakov IA, Krasnovskii AN, Kuznetsov AG (2017) The use of optimization algorithm for assessing effects of carboxyl functionalized MWCNTs on the productivity of nidltrusion process. J Nanostruct 7(2): 89-96.
- Kazakov IA, Krasnovskii AN, Kishchuk PS (2019) The influence of randomly oriented CNTs on the elastic properties of unidirectionally aligned composites. Mechanics of Materials 134: 54-60.
- Tandon GP, Weng GJ (1984) The effect of aspect ratio of inclusions on the elastic properties of unidirectionally aligned composites. Polymer Composites 5(4): 327-333.
- Tandon GP, Weng GJ (1986) Stress distribution in and around spheroidal inclusions and voids at finite concentration. Journal of Applied Mechanics 53(3): 511-518.
- Weng GJ (1984) Some elastic properties of reinforced solids, with special reference to isotropic ones containing spherical inclusions. International Journal of Engineering Science 22(7): 845-856.
- Wang YM, Weng GJ (1992) The influence of inclusion shape on the overall viscoelastic behavior of composites. Journal of Applied Mechanics 59(3): 510-518.
- Bogetti TA, Gillespie JW (1992) Process-induced stress and deformation in thick-section thermoset composite laminates. Journal of Composite Materials 26(5): 626-660.
© 2021 Kazakov IA and Krasnovskii AN. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version