- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Polymer Science: Peer Review Journal
The Non-Isothermal Curing Kinetics of One Epoxy Resin
Chen Peizhong, Fan Zepeng, Chen Yabo and Wang Kejian*
College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing, 100029, China
*Corresponding author: Wang Kejian, College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing, 100029, China
Submission: October 27, 2021;Published: November 11, 2021
ISSN: 2770-6613 Volume2 Issue3
Abstract
The non-isothermal curing kinetics of one epoxy resin was monitored by Differential Scanning Calorimetry (DSC). Based on the heat release curves at different heating rates, linear regression expression was obtained for the curing start temperature and the peak temperature by extrapolating the heating rate to be zero. The activation energy for curing was calculated by Kissinger and Ozawa models being an average value of 60.44kJ/mol while the reaction order was 0.892 by Ozawa formula. Thus, the n-order reaction kinetics equation was quantitatively determined for choosing reasonable dynamic heat rate and the optimal curing temperature range.
Keywords: Reaction kinetics; Curing; Epoxy resin; DSC
Introduction
As the matrix resin of high-performance fiber-reinforced composite materials, epoxy resin has been widely used in many fields such as aerospace due to its good adhesion, mechanical properties, and thermal properties. The curing reaction kinetics of epoxy resin system is an important foundation for theoretical basis and process guidance for the molding and manufacturing composite materials. This phenomenological method mainly uses some empirical model equations as the basic equations of curing reaction kinetics, where the values of parameters in model equation are calculated through mathematical fitting. Among them, the dynamic heating rate method is the most widely studied. Its basis is that the conversion rate of the resin at the exothermic peak temperature is a constant, independent of the heating rate [1]. Curing kinetic parameters such as apparent activation energy and reaction order play an important role in understanding the curing reaction. Generally, the Kissinger and Crane equations can be used to process the DSC data obtained at different heating rates, and the reaction kinetic parameters such as E, n, and A can be obtained, and then the n-order kinetic model equation of the curing reaction can be determined [2]. Here, the non-isothermal DSC curve is measured at different heating rate, from which the parameters of the cure kinetic equation is to be obtained by fitting calculation.
Materials and Apparatus
Epoxy resin (3232A) and its curing agent were purchased in market as described in [3]. This kind of epoxy is often used to prepare prepreg and compression-molded to cure at medium temperature for composite structures. Differential scanning calorimeter is DSC Q2000 of TA Instrument Company, USA. Electronic balance is of a precision of 0.001g.
Test Method
About 10mg of resin was weighed to be placed in ceramic crucible for DSC testing. Then, it was scanned from room temperature to 300oC under nitrogen gas at heating rates of 5K/min, 10K/min, 15K/min, 20K/min and 25K/min.
Results and Discussion
The DSC curves in heat flow versus temperature of different heating rates are shown in Figure 1. Single exothermic peak indicates that the resin undergoes an addition curing reaction during the heating process forming cross-linked structure [4]. It can be seen that the exothermic peak becomes steeper while the curing start temperature (Ti), the peak temperature (Tp) and the end temperature (Tf) shift to the higher temperature as the heating rate increases during curing. The main reason is that the epoxy resin reacts in lower activation in sufficient time at a lower heating rate resulting in three lower temperatures [4]. The area under curing peak becomes larger representing more heat being released during the reaction. Three typical temperatures of Ti, Tp and Tf are listed in Table 1. The data of Ti, Tp and Tf versus heating rate are drawn in Figure 2. The linear fitting values are close to the experimental data. The rising tendency for three typical temperatures at heating rate (β, °C/min) can be described by the linear fitting as Eq. 1.
Figure 1: DSC curves of Epoxy in curing at different heating rates.
Table 1: DSC data of resin system at different heating rates.
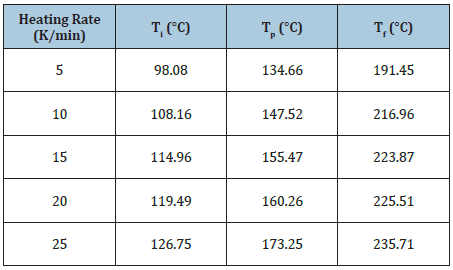
Figure 2: The data of Ti, Tp and Tf versus heating rate and the linear fitting.
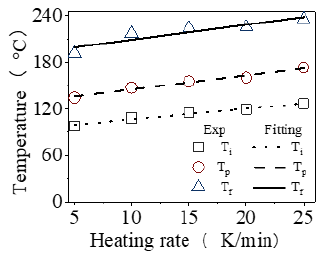
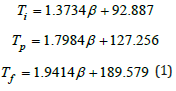
Three values are Ti0=92.887 °C Tp0=127.256 °C and Tf0=189.579 °C at β=0. Such extrapolation presents the temperature range. The upper limit temperature assuring nearly no curing is Ti0 for keeping it preventing gelation. The lower limit temperature assuring almost complete curing is Tf0 in preparing composite. No doubt, the curing temperature range between Ti and Tf can be determined at certain heating rate in addition to the peak temperature of Tp for fastest reaction. Tf can be referred to be the lower temperature for heat treatment [5]. Such optimal curing cycle is initially conducted by this linear regression at different heating rates. The peak temperature (Tq = TP + 273.15) in K changes with the Eq.2. (R, J∙mol-1∙ K-1) capable of being described by Kissinger equation and Crane equation [6,7]. The activation energy and frequency factor can be obtained by Kissinger equation as Eq.2.
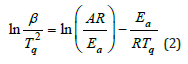
Where Ea is the apparent activation energy in J/mol, R is the ideal gas constant of 8.314J∙mol-1∙K-1. A is one frequency factor.
Figure 3 shows the relationship between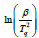 
and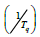 
at
different heating rates. Linear fitting gives the slope of the line,
which is -Ea/R. The intercept is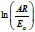 
and the correlation
coefficient is 0.96285. Thus, Ea=58.454kJ/mol and A=7.7112×106s-1
can be obtained. The reaction order in curing can be obtained by
Crane equation as Eq.3.
Figure 3: The curve of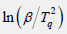 
versus (1/Tq).
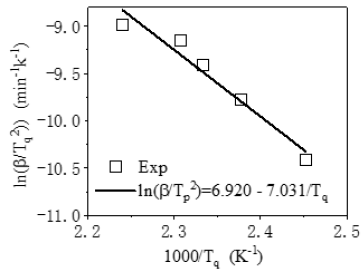
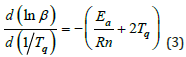
Ea/Rn≥2Tq is usually found to be true so that Eq.3 can be simplified to be Eq. 4.
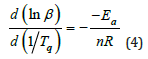
lnβ versus 1/Tq can be plotted to obtain the slope of the line as Ea/nR=7.884. Further, the reaction order in curing can be calculated being n=0.892 when substitute Ea=58.454kJ/mol and R into Ea/nR. The apparent activation energy of the curing reaction can also be calculated being Ea=62.428kJ/mol by the Ozawa equation of Eq.5.
It is higher than the ΔE obtained by the Kissinger method. The Ea calculated by the Kissinger method and the Ozawa method is averaged Ea=60.441kJ/mol. Besides, the reaction degree (α) varies with time at certain heating rate, which can be described by the kinetics models (Figure 4). Among them, one phenomenological model of the n-order kinetics is mostly adopted as Eq.6.
Figure 4: The curve of 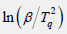versus (1/Tq).
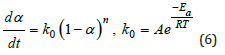
Where k0 is the reaction rate constant, which is temperaturedependent being written in Arrhenius equation. A is the exponential factor, also being frequency factor in Eq.2. Finally, the whole curing kinetic model in n-stage can be derived as Eq.7:
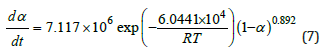
Eq.7 is used to predict the cure progress as shown in Figure 5. For comparison, the experimental data of the reaction degree (α) can be determined from heat flow curve in (Figure 1). The released reaction heat from the beginning to certain temperature can be obtained by integrating heat flow curve up to the corresponding time. At constant heating rate, the temperature is proportional to reaction time. α is the percentage of the released reaction heat to that in the overall reaction, represented by the peak area in DSC. In (Figure 5), the predicted cure degree (shown in curves) is close to the experimental data (shown in scattered points, illustrating the obtained kinetic equation of Eq.7 is really good for description of the Curing.
Figure 5: The predicted and experimental cure process at different heating rates.
Conclusion
The reaction kinetics equation was set up for one Epoxy through
calculation of curing parameters by Kissinger or Ozawa method
and Crane formula from the non-isothermal DSC curves.
a. The initial curing temperature (Ti), maximum exothermic
peak temperature (Tp) and curing end temperature (Tf) in DSC
curves under different heating rates were extrapolated to obtain
temperature range for the reasonable process.
b. Its activation energy (ca.60.441kJ/mol) and the frequency
factor (ca.7.117x106s-1) were calculated by the Kissinger or Ozawa
method from Tp in DSC curves. Crane formula is used to calculate
the reaction order (ca. 0.892).
c. The calculated values of kinetics parameters were put into
one n-order reaction kinetics model to form the reaction kinetics
equation, by which the predicted curing process is closed to the
data reflected from DSC curves.
References
- Gerami G, Bagheri R, Darvishi R (2019) Investigation of isothermal and dynamic cure kinetics of epoxy resin/nadic methyl anhydride/dicyandiamide by differential scanning calorimetry (DSC). Journal of Thermal Analysis and Calorimetry 137(2): 575-582.
- Chen C, Li YX, Gu YZ, Li M, Zhang Z (2018) An improved simplified approach for curing kinetics of epoxy resins by nonisothermal differential scanning calorimetry. High Performance Polymers 30(3): 303-311.
- Shen C (2002) The Determination of 3232 resin activation energy. Material Engineering 5: 191-194.
- Liu TS, Chen XB, Zhang BY (2005) Study on the cure kinetics of middle temperature curing 3234 epoxy resin system. China Journal of Aeronautical Materials 25(1): 45-52.
- Li YX, Chao C, Li T, Gu Y (2018) Establishment and verification of curing kinetics model of 603 epoxy resin system. Acta Materiae Compositae Sinica 35(1): 95-102.
- Crane LW, Dynes PJ, Kaelble DH (1973) Analysis of curing kinetics in polymer composites. Polymer Science 11(8): 533-540.
- Flores HA, Fasce LA, Riccardi CC (2013) On the cure kinetics modeling of epoxy-anhydride systems used in glass reinforced pipe production. Thermochimica Acta 573(2): 1-9.
© 2021 Wang Kejian. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version