About Models of Polymer Matrices Impregnation with Functional Additives in Supercritical Carbon Dioxide

The term “impregnation” is formulated in modern literature, dedicated to “green chemistry” as a diffusion of functional additive in carbon dioxide solution into polymer matrix not dissolved but swelled in it. The impregnation is a main method of functional material making by supercritical (SC) technologies. The catalytic, magnetic, luminescent, conductive, antifriction, materials for medicine and many others. The impregnation is complicated multy-factor process and concentration of functional additive (FA) in a polymer matrix depends on FA and a matrix chemical nature, on their compatibility, on solubility of FA in supercritical solvent (SCS), on the temperature, pressure, and duration of an experiment. Therefore, predictive estimates of the structure and composition of composites are not very accurate. To increase the accuracy of forecasting, in 1997 the first phenomenological model of this process was developed by the example of the impregnation of a polyester based on tere/isophthalic acid and bisphenol A (polyarylate DV) with the chemical formula

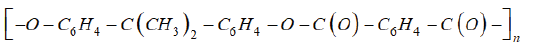
Polymer networks have a new physical property-elasticity, which substantially depends on their structure-the order of crosslinking of polymer chains. Classical polymer methods allow one to describe the elasticity of polymer networks only in a model assuming a tree structure of networks. Real polymer networks consist of a huge number of overlapping and interconnected polymer loops. Also, due to the randomness of the crosslinking process, the structure of polymer networks is random. Therefore, to describe them, it is natural to use the replica method, which allows one to calculate the elasticity of such polymer networks with loops and numerous defects of the topological structure [7,8]. Of particular interest in statistical physics and quantum field theory is the study of strongly fluctuating systems near the second-order phase transitions. To describe the “critical” fluctuations at different spatial scales in such systems, the renormalization group method was developed. Of course, polymer physics could not pass by such achievements! But in order not to frighten people, the words “renormalization group” were replaced by “scaling”, and the Gell-Mann-Low equations were replaced by “blobs”, from which, as from the original monomer units, polymer chains are assembled [9,10]. You should have seen the huge eyes of physicists in quantum field theory, to whom such exciting scaling concepts are reported! An interesting observation was made in the study of phase transitions from a disordered phase to a periodic crystal-like lattice. It turns out that the presence of a finite wave vector of the emerging superstructure suppresses fluctuations in such a system. Not surprisingly, this observation caused an avalanche of works on the theory of microphase separation in polymers, which continues even today [11]. Of course, unexpected analogies from other fields that can be adapted to describe polymers are not limited by the above list. Everyone can find something interesting. The main thing is not to forget that according to Murphy’s law “Everything is part of a larger system”. And this system is called Physics.

The kinetic curves of PD accumulation in the matrix increased linearly with a gradual reaching a plateau, which corresponded to normal diffusion according to Fick's law. However more careful the process investigation has shown that a diffusion in SC medium (SCM) has more complicate character and FA concentration after the maximum begins to decrease, reaching a certain minimum and again monotonously increases with reaching a plateau, after which it again falls. The model analyzes the curve including the plateau. The nature of the kinetic dependence in the model is explained as follows: the substance flow to the film surface and further to the depth arising due to the concentration gradient in the SC CO₂ solution and in the film is conventionally divided into two flows: diffusion due to the cymanthrene concentration gradient and drift-SC CO₂ flow with the dissolved complex due to the concentration gradient of SC CO₂. Since the diffusion coefficient of SC CO₂ (~10^–7cm²s^-1) is much larger than that of cytanthrene (~10^-10cm²s^-1), then the second flow in the polymer is always much larger than the first. Introducing into the polymer, SC CO₂ rapidly moves from all sides to the center, while cymanthrene accumulates in the surface layer. Having reached the middle of the film, the flow ceases and at the same time ceases accumulation of the FA the surface layer, the concentration of which at this moment is maximum and excess compared to equilibrium (Figure 1). Therefore, the cimanthrene layer then begins to dissolve and diffuses both inward and outward. This process corresponds to the falling section of the kinetic curve. The decrease in concentration occurs to a certain minimum value, determined by the competition of diffusion and relaxation of the matrix structure. At minimum point, there is already a new relaxed structure with its own characteristic sorption ability and, as a result, the absorption of the FA solution begins to increase again, gradually reaching a plateau, after which the whole picture of sorption is likely to repeat at a new relaxation level. This is the so-called “oscillating diffusion”, which is associated with the competition of the rates of diffusion and relaxation of the film structure. The model determines the mathematical expression for the concentration of FA at the extreme points of the kinetic curve and the time to reach the minimum point t_min and the plateau t₃. It was found that these times are proportional to h², but at the same time t min~C₀, and t₃≠f (C₀). Minimum initial solute concentration when it is still possible a formation of the surface layer with an excess concentration of the substance is determined by the formula . The equilibrium amount of the impregnated substance, the normalized initial value does not depend on С₀ and h, while the minimum value .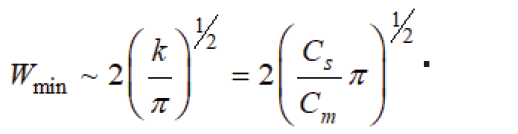

Figure 1: Kinetics of unsteady-state diffusion of CpMn (CO)3 in SC CO2 solution into polyarylate film and images of impregnation stages. Fdiff-diffusional flow, Fdrift -drift flow, CpM-CpMn (CO)3.

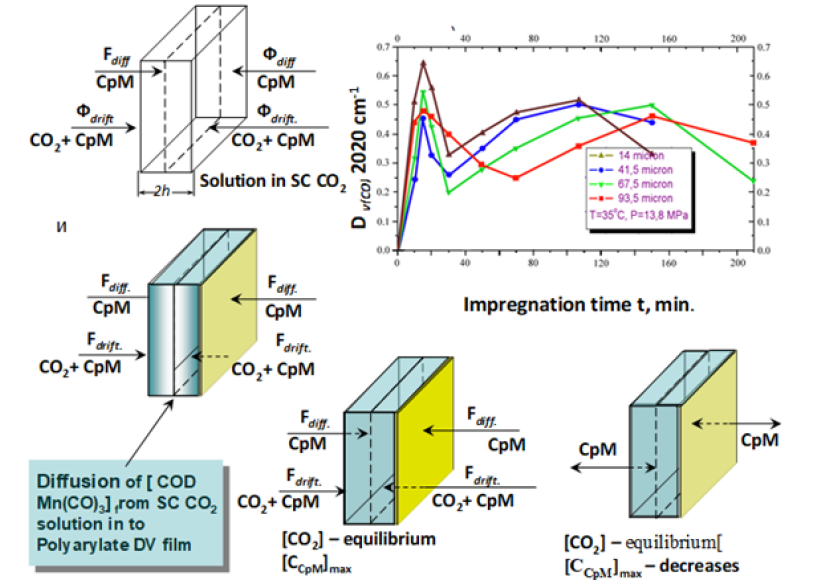
The absolute value of the impregnated FA A~h, also depends on the initial concentration as (C₀)^3/2 at t=t_min and ~C₀ at the plateau level (t>t₃). K^-1 is the degree of supersaturation of the surface layer relative to Cs, the equilibrium concentration of FA in the film. C_m is the concentration of FA in the surface layer, h is the film thickness, l is the thickness of the surface layer, D₁ is the diffusion coefficient of CpMn(CO)₃ in the film in the presence of SCM, D₂ is the diffusion coefficient of SCM in the film, C₀ is the concentration of FA in the SCM solution, C₁ is the maximum weight concentration of CO₂ in the polymer. The concentration of FA on the plateau matches ~C_S. The ratio . An important conclusion follows from the model: non-stationary diffusion is observed only at high solubility of FA in SCM. At low solubility (10^–4-10^–6 mol/L), the maximum at the kinetic curve is initially absent (since there is a lack of equilibrium concentration of FA in the solution to create an excess concentration in the surface layer of the film and the kinetic curve is monotonous. This conclusion we tested and confirmed during the impregnation of Red13 dye into a DV polyarylate film [3]. The concentration boundary of the transition from one type of impregnation to another is currently unknown and requires a special definition for each FA. Since the first maximum on the kinetic curve is reached in 15-20 minutes, it is possible by repeated impregnation for 20 minutes followed by rapid decompression to create a large concentration of FA in the surface layer.

The described model, despite its shortcomings (it does not take into account matrix swelling in SCM), is by far the most detailed mathematical representation of FA impregnating process (on the example of an organometallic complex) into a polymer matrix and can be used after experimental verification of the main conclusions and additional modernization for quantitative forecasting of the impregnation process. In the future, it can serve as the basis for the transfer of impregnation in SCM from art to technology. Therefore, it would be extremely important to experimentally verify all the quantitative conclusions of the model. This work would stimulate the solution of the most important problem - the development of industrial impregnation processes in SC CO2 and more generally in SCM.

The work was supported financially by the Ministry of Science and Higher Education of the Russian Federation.

1. Sobol EN, Bagratashvili VN, Popov VK, Sobol AE, Said Galiyev EE, et al. (1998) J Phys Chem (Russia) 72(1): 23.
2. Houdle SM, Qun L, Popov VK, Bagratashvili VN, Sobol EN (1997) Proc IV Intern Symp Supercritical Fluids. Sendai; Japan. p. 259.
3. Sobol EN, Bagratashvili VN, Sobol AE, Khodl SM (1997) Reports of the Russian Academy of Sciences. 356(6): 777.
4. Said Galiev EE, Gornov EA, Vinokur RA, Nikitin LN, Gamzazade AI, et al. (2006) Supercritical Fluids: Theory and Practice. 1(2): 69.