Investigation of the Effect of External Local Sealing Loads on the Well Support

The main cause of deformation is the formation of fluid in the annulus between the casing and tubing. After freezing, this liquid changes from liquid to solid. The pressure then destroys the casing lining and cement sheath. In general, this opinion is correct. However, the studies do not include the propagation of lateral and normal stresses in cement, as well as the effect of the presence (or absence) of adhesion, as well as the effect of these elements on the strength of the entire structure. The above facts and the occurrence of problems in operation became the reason for the study [1]. The main reasons for the formation of the sealing external pressure are the freezing pressure in permafrost and its pressure in the zone of rock flow. As a rule, this pressure is local, therefore it obeys the mechanics of a continuous medium [2].

The limiting state of the casing string can be characterized by the occurrence of plastic deformation in the inner casing, which is preceded by collapse. Moreover, it retains the loadbearing capacity. The casing and cement sheathing of other pipes bonded together will be in an elastoplastic or plastic region. During volumetric compression of the cement sheath, it is transformed into an elastoplastic material [3]. Thus, the strength of the casing support is increased by converting the entire system from brittle to ductile. The entire process of material destruction begins with micro cracks. The plastic layer of one of the materials does not turn into the second layer until it reaches the stress limit. When the layer in the casing lining passes into the plastic stage, then the total pressure completely passes through this layer to the next layer. Currently, there are a large number of varieties of the elastic and plastic range of casing pipes and cement sheath, and in general depends on the pressure value, design features of the casing string and the physical and mechanical characteristics of its layers. Initially, in the zone of elastoplastic deformations, the outer casing is distributed along the pipe, and then along the rest of the casing [4]. The value of pressure in the elastoplastic region and the plastic region of the well casing and cement sheath is based on solving a system of equations.

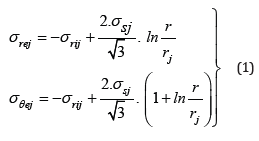
It is equivalent for all layers of the well casing at the interface of the formation boundaries and during the transition from elastic to plastic (rj ≤r≤ ρj). where ρj -radius of plasticity; σrjj -radial pressure in the inner regions of the outer pipe and cement; σ(rj+1) - radial pressure of the material yield point in the jth layer [5]. (Table 1) shows the bearing capacity of the casing in the zones of elastoplastic and plastic deformations. At these values, plastic regions of various sizes are formed in the casing of a three-column well structure [6]. (Table 1) presents two options for the results. The first one has a modulus of elasticity Е1=1*103MPa for cement between the casing pipes. The second has Е2=1*104MPa. As can be seen from (Table 1), the external pressure of the casing support in the elastoplastic deformation zone is higher than in the elastic deformation zone. However, the spread of the plasticity zone in the casing pipes of the lining leads to uneven loading or loss of stability. As a result, this leads to a serious well accident. In connection with the calculation data, the resistance to casing collapse is based on its tests in the elastic deformation zone [7]. The creation of a mathematical model of the bending of a complex well design can be represented in the form of differential equations of a single-level design [8].

Table 1:Calculated values of external pressure.

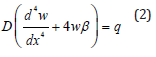
Where D - integral characteristic of the bending stiffness value of a complex well structure; w(x) - bending function, m; q - local load of pressure distribution in the investigated area, MPa; For one of the layers, this expression can be transformed into the following equation:

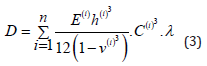
The first of the terms is represented by the stiffness value of a simple well structure, and the second provides for the strength of the bond between the columns [9]. Where λ -modular value of the ratio, which can be expressed from the following equation:

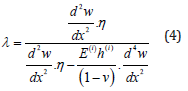
where C(i)-distance between the centers of adjacent layers on the surface of the borehole wall, M; E(i)- modulus of elastic i-layer; ν(i)-poisson’s ratio for material of i-layer; h(i)-thickness of the i-layer, m; R-the radius of curvature of the shell, m; η-coefficient of adhesion shear stiffness at the contact of a cement-filling pipe, N/mm3.

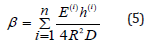
Bending of a compound cylindrical shell is performed on the lateral faces of the structure for the condition of a hinged support [10]. The deflection function is presented as a system of sinus functions W(x) (6):

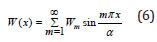
Deformation in the range of the line (7):

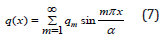
Thus, it is possible to calculate radial deformations (8);

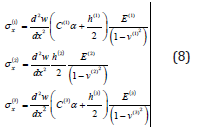
Where α-length in the area of local deformation [11].

The tangential shear stress at the boundaries of the adjacent layer is written by the following expression:

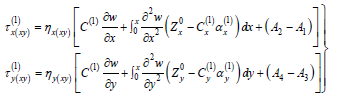
Where Am-constants depending on the boundary conditions of the layer attachment [12]. Thus, according to the solution of the equations, it is possible to determine the magnitude of the local sealing loads on the investigated section of the well of a complex design.

The difference in constants is represented as Am+1 + A1 = 0

For 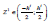is the coordinate of the point Bi - the layer in which the stress state components are formed. Let’s look at an example. (Figure 1) shows a computational model of the stress-strain state of wells with a complex casing support structure under a local axisymmetric load. (Figure 1) shows the graphs of the propagation of normal and shear stresses in the casing and cement sheath. This example shows that the force of external pressure increases at the point of compaction of the contact of the cement with the casing of the well.

Figure 1: Calculation model of th e stress-strain state of the casing string under the local axisymmetric load.

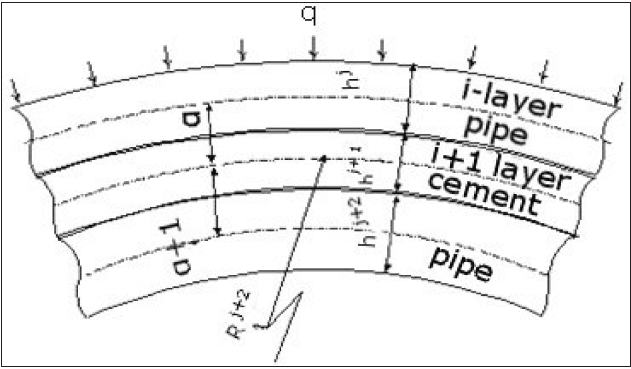
Main significant coefficients:
h(1), h(2) и h(3) - thickness of cement and pipe walls;
Е(1), Е(3) и Е(2) - the modulus of elasticity of the pipe material and cement stone.
The values of the lower and upper levels of the casing wall thickness are taken from the standards, and the elastic modulus of the cement is in accordance with [13].
h(1)=h(3)=8,9*10-3m; h(2)=29,6*10-3m; R=98,8*10-3v;
Е(1)=Е(3)=2,1*105MPa; a=12,0m; C(1)=C(2)=23,7*10-3m; q=50MPa;
η=0,100, 106; N/mm3; Е(2)=103; 5*103; 1*106MPa.
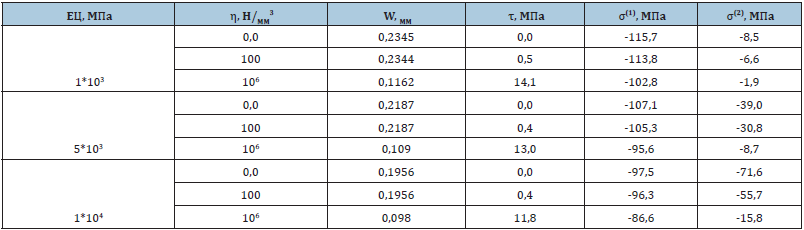
The maximum values of the parameters of the stress-strain state of the well support are shown in (Table 2).

Table 2:Basic calculation parameters.

The result of the study scientifically proves that the main local sealing load is experienced by the well support section in the interval of 0.4÷0.6 x/a, that is, near the application of local pressure application. As an example, a section was considered at the point x/a=0.5. At each section of the well support, the loads reach different values and do not depend on the adhesion of the cement stone to the casing and its strength properties. In the presence of a strong compaction of the cement stone with the casing, the values of normal compressive stresses in the cement stone are much lower than in its absence, and the higher the mechanical strength of the cement stone, the higher the magnitude of the resulting compression stresses, which indicates a special distribution of the local load by the well support elements. The study showed that the arising local stresses in absolute value in the casing are significantly higher than in the cement ring. In the case of tight adhesion of the cement stone to the casing, the system perceives the load as a whole, and the value of the mechanical strength of the cement stone significantly affects the value of the created compressive stress. In the first case, they reach 100MPa.

In the second case, the picture is the opposite. In the absence of adhesion of the casing to the cement, the maximum value of normal stresses along the cement ring can reach about 70MPa. The resulting local sealing loads weaken the casing, which leads to accidents at the well. The nature of lateral stress propagation is more complex. First, in this case there is no dependence of the mechanical strength of the stone. Secondly, it has a wavy character, which is explained by the different directions of their actions (clockwise or counterclockwise). As a result, the propagation of the arising local sealing stresses manifests itself on the deflection of the well support. In this case, the deflection is noted at a distance of about ±0.15x/a from the point of application of the crushing load. Of particular importance is the presence of adhesion between the casing and the cement stone. The modern improvement of the well cementing technological process is to ensure a strong contact formed in the annulus. Thus, as a result of theoretical studies and calculations, it can be assumed that the occurrence of complications caused by external local crushing loads is associated with the formation of normal stresses in the casing and cement stone. In absolute value, they can exceed the mechanical strength indicators of the elements of the “casing-cement stone” system.

1. Gerasimov DS (2017) Scientific and technical inspection of methods for selecting casing strings when exposed to local and uniformly distributed loads. Russia, pp. 1-211.
2. Kuznetsov VG (2003) Stress-strain state of well support in permafrost zone: Section. pp. 1-154.
3. Pavelyeva ON (2018) Development of technologies and technical means for the construction of wells intended for the production of high-viscosity oils. Abstracts of the III International Scientific and Practical Conference. Drilling Wells in Complicated Conditions. Russia, pp. 102-104
4. Pavelyeva ON, Pavelyeva NY, Parshukova LA, Ovchinnikov VP (2020) Changes in filtration properties in reservoir rocks during drilling. Journal Subsoil Use 1(83): 64-69.
5. Pavelyeva ON, Pavelyev NY, Ovchinnikov VP Change of filtration properties in rocks of collectors during drilling. Lap Lambert Academic Publishing Germany, pp. 415.
6. Pavelyeva ON, Golozubenko VA (2019) Investigation of the conditions for efficient drilling of wells at development targets with hard-to-recover reserves. Collection of scientific papers based on the materials of the II International Scientific and Practical Conference. Science Society Man, Russia, pp. 23-25.
7. Pavelyeva ON (2019) Modern technologies and techniques for influencing high-viscosity oil and natural bitumen deposits. materials of the international scientific-practical conference of young researchers named after Mendeleev DI, dedicated to the 10^th Anniversary of the Institute of Industrial Technologies and Engineering, Russia, pp. 417-418.
8. Pavelyeva ON (2019) Improving the reliability of construction of wells intended for the production of high-viscosity oils. Materials of the International Scientific-Practical Conference of Young Researchers Named after Mendeleev DI, Dedicated to the 10^th Anniversary of the Institute of Industrial Technologies and Engineering, Russia, pp. 415-416.
9. (1999) Methodology for choosing a well design in a frozen zone. Russia, p. 31.
10. Ovchinnikov VP (2018) Construction of wells in the fields of the shelf of the seas and oceans: Textbook. Russia, pp. 370.
11. Shemelina ON (2020) Basic principles of drilling in the Bazhenov formation. Journal Bulanovskie Readings 3: 377-379.
12. Shemelina ON (2019) Modern problems of oil drilling. Materials of the IX International Scientific and Practical Conference. To the Heights of Knowledge, Russia, pp. 128-130.
13. Ovchinnikov VP, Rozhkova OV, Ovchinnikov PV, Shemelina ON (2019) High viscosity oil development technology. International Journal of Petroleum Technology 6: 35-40.