Important Keys in the Estimation of Parameters During Hydrocracking Kinetic Modelling

Hydrocracking has emerged as one of the most important secondary petroleum refinery processes due to increased heavy crude production and high demand for valuable products. For this reason, in recent years, researchers have sought to develop refining techniques based on feedstock available at low prices, such as heavy oil, bitumen and residues. The objectives of upgrading these feeds are to decrease the viscosity and the boiling point, reduce or eliminate the level of impurities (such as metals and nitrogen and sulfur compounds) and increase the H/C ratio. To achieve these objectives, dispersed metallic catalysts are used, but to understand the catalytic behavior inside the reactor, reaction mechanisms represented by kinetic models are used where detailed reaction parameters, that depend mainly on the catalyst, feed and operating conditions are optimized [1,2].

When we talk about heavy crude oils and bitumens, their complex composition complicates the kinetics of hydrocracking because they contain a wide variety of impurities as well as high molecular weight materials such as asphaltenes. Nevertheless, that is not all, but also the colloidal structure influences the general kinetics, such as the interaction between the micelles of resins and asphaltenes that must disintegrate to allow the hydrocracking reactions to continue [3].

In hydrocracking, asphaltenes or large compounds are broken to form low molecular weight compounds over a catalyst in a hydrogen-rich atmosphere. Simultaneously, another reactions taking place are hydrodesulfurization, hydrodemetallization, etc., and the different rates and selectivity of each reaction depend on the properties of the catalyst used and on the reaction conditions [1]. While cracking reaction is endothermic, the hydrogenation is exothermic leading to an overall exothermic hydrocracking process, since the heat required for cracking is less than the heat released during hydrogenation. Generally, both thermal and catalytic reactions were considered to occur in parallel [4].

Kinetic modeling of hydrocracking of heavy petroleum fractions is often performed in lumped to simplify the feedstock that contains a large number of hydrocarbons. A considerable number of models have been proposed, which consist of a limited number of pseudocomponents (usually less than 10) [5,6]. The benefits of traditional and discrete lumping methods lie in their simplicity since with relatively few equations to solve and few parameters to estimate, calculation times are low. However, the number of pseudocomponents can be increased to make better use of the experimental data, but this exponentially raises the number of reaction rate parameters to estimate [7].

The precision of kinetic data can be affected by several factors such as cumulative error in the measurement of experimental parameters. In addition to the usual parameters such as temperature, H2 pressure, space velocity and/or contact time, the type of experimental system and the time in which the measurement is taken must be considered because the data values will change over time due to gradual deactivation of the catalyst [3].

Reaction kinetics data obtained under conditions of mass transfer limitations cannot be used as such for setting meaningful kinetic expressions because mass transfer limitations can mask the results and lead to misinterpretations in developing kinetic models. There are some criteria for performing kinetic experiments under conditions where transport resistances are negligible depending on the reactor system. When these conditions are ensure, intrinsic kinetic equations will be obtained and reaction kinetic parameters (rate constant, activation energies, and collision factors) will be optimal estimated, so it is important to perform kinetic experiments under conditions where transport resistances are negligible. In addition, there are many correlation in order to ensure the well diffusion of reactive and product molecules [8,9].

As seen in any reaction, the diffusion of reagent molecules into the pores of the catalyst as well as the diffusion of product molecules out of the pores, affect the rate of hydrocracking reactions. Therefore, another important factor to consider during kinetic studies is the porosity of the catalyst (for supported catalyst). In the case of residues and heavy crude oils, the volume and size distribution of the pores are important parameters, since they are affecting the effective diffusivity of the reactant molecules (mainly asphaltenes) when the diameter of these molecules are close to the diameter of the catalyst pores [3].

Hydrogen is frequently omitted from kinetic expressions and a sufficiently high concentration of H2 in liquid phase has to be maintained to ensure a desirable rate of hydrogen activation by catalyst surface. There is always an optimal H2S/H2 ratio where the supported catalysts (which are the catalysts commonly used in hydrocracking) exhibit their highest activity, so the presence of H2S in the hydrocracking streams is desirable to keep the catalyst in active form. The main mechanism of action in hydrogenation reactions is when H2 gas is activated (separated) on the surface of the catalyst, so it is the active hydrogens that play a key role in hydrocracking reactions and not H2 gas. Due to the excess of hydrogen, almost all researcher assumed that the reactions during hydrocracking are pseudo-first order. This assumption also allows to solve more easily the system resulting from the ordinary differential equations that represent the different models [3,10].

In addition, it is important to verify that indeed the order of reaction assumed in the kinetic model is the appropriate one and this is done by graphing the variation of the conversion with respect to time in the appropriate power law model according to our reaction system. In Figure 1 Félix G, et al. [11] verified the reaction order of the kinetic model from experimental data obtained in a batch reactor by plotting the ln (1/(1−XR)) versus the reaction time at different reaction temperatures, obtaining a straight line indicating that the reaction order assumed was indeed 1.

Figure 1: Confirmation of the kinetic model firstorder reaction at different temperatures [11].

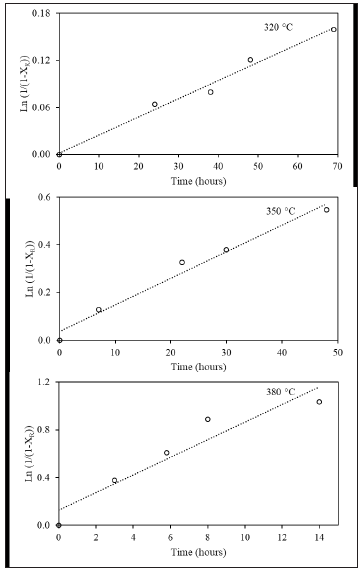
The parameter estimation process is somewhat complicated since most of the models have a high number of parameters to estimate in which multiple solutions can be obtained due to their high non-linearity. That is why many times during the parameter optimization process it is not possible to guarantee the estimation of the optimal values of these parameters. There are many optimization techniques. Linear or nonlinear regressions are used to calculate kinetic rate constant from measured rates and concentrations. However nonlinear optimization is the most popular approach and is commonly used to estimate the best values of kinetic parameters [12,13].

Only a few kinetic studies reported in the literature provide sufficient evidence to guarantee that the parameter values correspond to the global minimum of the objective function (differences between the experimental and calculated value). Sensitivity analysis is a tool that allows to confirm that the parameter values obtained by regression are optimal. This analysis is based mainly on changing the value of the calculated parameters after optimization (one at a time) due to disturbances in the obtained value, calculating again the objective function for each change. If all the disturbed parameters give the minimum of the objective function at 0% (original value) disturbance, the parameters are optimal [11].

Félix G, et al. [11] shows the difference when the sensitivity analysis is applied to the kinetic modeling to optimized the kinetic parameter. The reaction rate coefficients when the sensitivity analysis is not applied gave a not good fit of the calculated data to experimental data than those where the sensitivity analysis is applied Figure 2. This shows that the estimation of parameters based on sensitivity analysis is a powerful tool to confirm that the estimated values of the parameters are optimal. Therefore, this analysis indicates if the parameters were estimated wrongly and find the best parameters for our experimental data, which represent the reaction mechanism well.

Figure 2: Comparison of the calculated data when the sensitivity analysis is applied (x) and not applied (o) to the kinetic modeling to optimized the kinetic parameter [11].

1. Ancheyta J, Sánchez S, Rodríguez MA (2005) Kinetic modeling of hydrocracking of heavy oil fractions: A review. Catal Today 109(1-4): 76-92.
2. Sahu R, Song BJ, Im JS, Jeon YP, Lee CW (2015) A review of recent advances in catalytic hydrocracking of heavy residues. J Ind Eng Chem 27: 12-24.
3. Marafi A, Stanislaus A, Furimsky E (2010) Kinetics and modeling of petroleum residues hydroprocessing. Catal Rev Sci Eng 52(2): 204-324.
4. De Almeida RM, Guirardello R (2005) Hydroconversion kinetics of marlim vacuum residue. Catal Today 109(1-4): 104-111.
5. Asaee SDS, Vafajoo L, Khorasheh F (2014) A new approach to estimate parameters of a lumped kinetic model for hydroconversion of heavy residue. Fuel 134: 343-353.
6. Becker PJ, Serrand N, Celse B, Guillaume D, Dulot H (2016) Comparing hydrocracking models: Continuous lumping vs single events. Fuel 165: 306-315.
7. Browning B, Afanasiev P, Pitault I, Couenne F, Fayolle MT (2016) Detailed kinetic modelling of vacuum gas oil hydrocracking using bifunctional catalyst: A distribution approach. Chem Eng J 284: 270-284.
8. Mederos FS, Ancheyta J, Chen J (2009) Review on criteria to ensure ideal behaviors in trickle-bed reactors. Appl Catal A: Gen 355(1-2): 1-19.
9. Perego C, Peratello S (1999) Experimental methods in catalytic kinetics. Catal Today 52(2-3): 133-145.
10. Félix G, Ancheyta J (2019) Comparison of hydrocracking kinetic models based on SARA fractions obtained in slurry-phase reactor. Fuel 241: 495-505.
11. Félix G, Ancheyta J, Trejo F (2018) Sensitivity analysis of kinetic parameters for heavy oil hydrocracking. Fuel 241: 836-844.
12. Jarullah AT, Mujtaba IM, Wood AS (2011) Kinetic parameter estimation and simulation of trickle-bed reactor for hydrodesulfurization of crude oil. Chem Eng Sci 66(5): 859-871.
13. Sámano V, Tirado A, Félix G, Ancheyta J (2020) Revisiting the importance of appropriate parameter estimation based on sensitivity analysis for developing kinetic models. Fuel 267.