- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Progress in Petrochemical Science
A Review on Magneto Hydrodynamic Fluid Flows
Padmavathi RS 1, Raju MC 2* and Venkateswarlu S3
1 Department of Mathematics, JNT University, India
2 Department of Mathematics, Annamacharya Institute of Technology and Sciences, India
3 Department of Mathematics, RGM College of Engineering, India
*Corresponding author:Raju MC, Department of Mathematics, Annamacharya Institute of Technology and Sciences Rajampet (Autonomous), Cuddapah, India
Submission: July 16, 2018;Published: July 20, 2018
ISSN 2637-8035Volume2 Issue4
Abstract
In this review article a detailed study is presented on magneto hydrodynamic flows and their importance. Basic concept of MHD is discussed in detail. The results of various researchers are presented and addressed properly
Keywords:MHD; Basic equations of MHD; Convective flows
Introduction
The interaction of electromagnetic fields and fluids may be described from a scientific point of view, by the proper application of the principles of the special theory of relativity. The practical application of these principles, to actual physical phenomena of engineering, Astrophysics, Geo-physics, etc., is important in recent years. The study of this application to continuum has become known as magneto hydrodynamics or magneto fluid mechanics. The studies of magneto hydrodynamics of viscous conducting fluids play a significant role during the recent times, owing to its practical interest and abundant applications in astro-physical and geo-physical phenomenon. Astrophysicists and geo-physcists realized soon after the advent of special relativity theory that electromagnetic fluid interactions were of great importance in stellar and planetary processes. The main impetus to the Engineering approach to electromagnetic fluid interaction studies has come from the concept of the MHD direct conversion generation, propulsion studies of radio propagation in the ionosphere, and controlled nuclear fusion. The study of flow problems of electrically conducting fluid particularly of ionized gases is currently receiving considerable interest.
Such studies have made for many years in connection with astro-physical and geo-physical such as sun spot theory, motion of the interstellar gas etc. In recent years some Engineering problems need the studies of the flow of an electrically conducting fluid. Devika et al. [1] introduced the problem an analysis of first order homogeneous chemical reaction and heat source on MHD oscillatory flow of a visco-elastic fluid through a channel filled with saturated porous medium are reported. The present visco-elastic fluid model is working to suggest rheological liquids encountered in biotechnology (medical creams) and chemical engineering. This rheological model introduces additional terms into the momentum equation. It is assumed that the fluid has small electric conductivity and the electromagnetic force produced is very small. The dimensionless governing equations are solved analytically using regular perturbation method. The effects of various parameters on velocity, temperature and concentration fields are presented graphically and discussed. Raju et al. [2] discussed the problem of MHD free convective, dissipative boundary layer flow past vertical porous surface in the presence of thermal radiation, chemical reaction and constant suction, under the influence of uniform magnetic field which is applied normal to the surface is studied. The governing equations are solved analytically using a regular perturbation technique. The expressions for velocity, temperature and concentration fields are obtained.
With the aid of these, the expressions for the coefficient of skin friction, the rate of heat transfer in the form of Nusselt number and the rate of mass transfer in the form of Sherwood number are derived. Finally, the effects of various physical parameters of the flow quantities are studied with the help of graphs and tables. It is observed that the velocity and concentration increase during a generative reaction and decrease in a destructive reaction. The same observed to be true for the behavior of the fluid temperature. The presence of magnetic field and radiation diminishes the velocity and also the temperature. Ravikumar et al. [3] studied the problem of unsteady, two-dimensional, laminar, boundary-layer flow of a viscous, incompressible, electrically conducting and heatabsorbing Rivlin-Ericksen flow fluid along a semi-infinite vertical permeable moving plate in the presence of a uniform transverse magnetic field and thermal buoyancy effect is considered.
The plate is assumed to move with a constant velocity in the direction of fluid flow while the free stream velocity is assumed to follow the exponentially increasing small perturbation law. Time-dependent wall suction is assumed to occur at the permeable surface. The dimensionless governing equations for this investigation are solved analytically using two-term harmonic and non-harmonic functions. The obtained analytical results reduced to previously published results on a special case of the problem. Numerical evaluation of the analytical results is performed and some graphical results for the velocity and temperature profiles within the boundary layer are presented. Skin-friction coefficient, Nusselt numbers are also discussed with the help of the graphs. Raju et al. [4] investigated the problem a steady MHD forced convective flow of a viscous fluid of finite depth in a saturated porous medium over a fixed horizontal channel with thermally insulated and impermeable bottom wall in the presence of viscous dissipation and joule heating.
The governing equations are solved in the closed form and the exact solutions are obtained for velocity and temperature distributions when the temperatures on the fixed bottom and on the free surface are prescribed. The expressions for flow rate, mean velocity, temperature, mean temperature, mean mixed temperature in the flow region and the Nusselt number on the free surface have been obtained. The cases of large and small values of porosity coefficients have been obtained as limiting cases. Further, the cases of small depth (shallow fluid) and large depth (deep fluid) are also discussed. The results are presented and discussed with the help of graphs. Priya et al. [5] discussed the combined effects of radiative heat transfer and a transverse magnetic field on steady rotating flow of an electrically conducting optically thin fluid through a porous medium in a parallel plate channel taking hall current into account and non-uniform temperatures at the walls. The analytical solutions of velocity, temperature, shear stresses and rate of heat transfer are obtained from coupled nonlinear partial differential equations for the problem. The computational results are discussed quantitatively with the different variations in dimensionless parameters entering in the solution. Ravi et al. [6] found a perfect solution to the present natural convective flow problem of a vertical transfinite plate owing to the impulsive motion in the ubiety of first ordered chemical reaction, radiation absorption, radiation, Newtonian heating and species concentration in its plane is evolved by applying the method of Laplace transforms in closed form at the plate.
Exact results for velocity, temperature, concentration fields are prevailed and expressions for heat and mass transfer rates are also found. The effects are analyzed for the respective invariables for both ammonia and water vapor. Misra et al. [7] considered the problem of oscillatory MHD flow of blood in a porous arteriole in presence of chemical reaction and an external magnetic field has been investigated. Heat admass transfer during arterial blood flow is also studied. A mathematical model is developed and analyzed by using appropriate mathematical techniques. Expressions for the velocity profile, volumetric flow rate, wall shear stress and rates of heat and mass transfer have been obtained. Variations of the said quantities with different parameters are computed by using Mathematica software. Ramaiah et al. [8] considered the combined influence of chemical reaction and radiation absorption effects on hydro magnetic free convective heat and mass transfer flow of viscous, in-compressible, electrically conducting visco-elastic fluid through porous medium bounded by an oscillating porous plate in the presence of heat sources is studied.
The expressions for velocity, temperature and concentration distribution, skin-friction, rate of heat and mass transfer coefficients at the plate are obtained using perturbation technique. The effect of various physical parameters occurring into the problem on velocity field is discussed with the help of graphs. Joseph et al. [9] considered the effect of variable suction on unsteady MHD oscillatory flow of Jeffrey fluid in a horizontal channel with heat and mass transfer has been studied. The temperature prescribed at plates is uniform and asymmetric. A perturbation method is employed to solve the momentum and energy equations. The effects of various dimensionless parameters on velocity and temperature profiles are considered and discussed in detail through graphs. It is found that, the velocity increases with increase in ℎ2, 1, Gr, Gc, N, Re and Sc. The velocity also increases with decrease in ℎ1, a2, Ha and Kc. It is also observed that the temperature increases with increase in N and Pe. Increase in Schmidt number Sc and chemical parameter Kc respectively increase and decrease the species concentration or the concentration boundary layer thickness of the flow field.
Maruf Hasan et al. [10] concentrated on the analysis of MHD free convection flow past an inclined stretching sheet. The viscous dissipation and radiation effects are assumed in the heat equation. Approximation solutions have been derived for velocity, temperature, concentration, Nusselt number, skin friction and Sherwood number using Nachtsheim-Swigert shooting iteration technique along with the six-order Runge-Kutta iteration scheme. Graphs are plotted to find out the characteristics of different physical parameters. The variations of physical parameters on skin friction coefficient, Nusselt number and Sherwood number are displayed via table. Falade et al. [11] investigated the effect of suction/injection on the unsteady oscillatory flow through a vertical channel with non-uniform wall temperature. The fluid is subjected to a transverse magnetic field and the velocity slip at the lower plate is taken into consideration. Exact solutions of the dimensionless equations governing the fluid flow are obtained and the effects of the flow parameters on temperature, velocity profiles, skin friction and rate of heat transfer are discussed and shown graphically. It is interesting to note that skin friction increases on both channel plates as injection increases on the heated plate.
Electromagnetic Body Force
The basic concept on electromagnetism is Coulomb’s law for the force on charged particles in an electrical field. Coulomb’s law states that the force on charged particles is proportional to the product of the charge on the particle and the local electric field seen by the particle. In the rest frame of the particle and in RMKS units the law is stated as
figure :
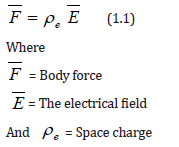
When a charged particle moves in the presence of arbitrary electric and magnetic fields, the resulting force is called Lorentz force, which can be written as
figure :
The equation (1.2) is valid in any frame of reference, either in the rest frame (local frame of reference at rest with respect to the fluid) or the laboratory frame. The electromagnetic body force results from the Coulomb force. The general quasi-state body force density for linear homogenous media can be written in the rest frame as
figure :
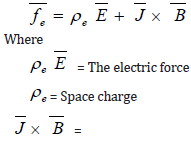
The interaction force between the current and magnetic field. Which becomes the redominant force in magneto fluid dynamics? This is called ponder motive force.
Basic MHD Equations
The electromagnetic body force acts on the fluid and in turn the motion of the fluid in the presence of the electromagnetic field may generate an induced electromagnetic field and alter the field. Thus, the velocity field in the fluid and electric and magnetic fields inside the fluid are disturbed due to the interaction of the fluid forces and the external electromagnetic force. We must combine the basic concepts of fluid dynamics and electromagnetism to discuss the magneto fluid dynamics. The equations governing motion will be the Navier-Stokes equation of fluid and Maxwell’s equations, which are usually coupled and must, solved simultaneously. The electromagnetic body force is usually non-conservative (rotational) and not derivable from a scalar potential function. Only under rare circumstances it may be approximately conservative and derivable from a scalar potential function. In such cases the electromagnetic body force alters simply the pressure, provided the boundary conditions on velocity and pressure remain the same. However this happens in exceptional cases and the force is rotational in general and does alter the flow.The Maxwell’s equations in RMKS units are
figure :
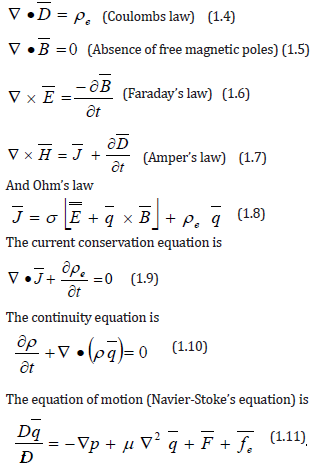
These equations hold in any frame of reference.
MHD approximations
In additions to the non-relativistic approximation, certain additional simplifications can be made for flow, which is quasisteady (steady or low frequency oscillatory), and in which the electric field is of the order of magnitude of the induced quantity
figure :
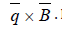
Elsasser has pointed out that the ratio of the displacement current to the conduction current in large class of phenomena is so small that displacement current can be neglected entirely. Thus, both space charges and the electrostatic potential are omitted.
The following assumptions are made under MHD approximation.
figure :
(1)
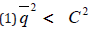
This allows the quantity
figure :
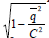
to be taken as unity and use the non-relativistic Newtonian form of equations of motion, where c is the velocity of the light.
(2) The electric field E is of the same order of magnitude as the induced electric field
figure :
This assumption allows us to assume that the induced magnetic field is much smaller than the externally applied magnetic field.
(3) The problems of very high frequency are not considered, so that the displacement current
figure :
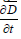
is neglected compared to J , the conduction current.
Thus, the equations of electromagnetic fields (1.6) and (1.7) become
figure :
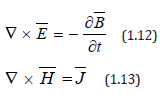
Equations (1.12) and (1.13) are called pre-Maxwell equations for electromagnetic fields. (4) The electric energy is negligible compared to the magnetic energy. Since the displacement current and electric field energy are neglected, the main interaction is between the magnetic field and the fluid. (5) The current density vector J is approximately the same in any inertial frame. This means using Ohm’s law we get
figure :
(6) The magnetic force density represented by
figure :
The electric term can be shown to be negligible compared to magnetic term. For this reason, the term
figure :
is often neglected in MHD.
figure :
figure :
Also
is valid even for high frequency phenomena if the fluid velocity q is very small compared to c.
Equations Under the MHD Approximation
The basic equations under the MHD approximation take the following form.
figure :
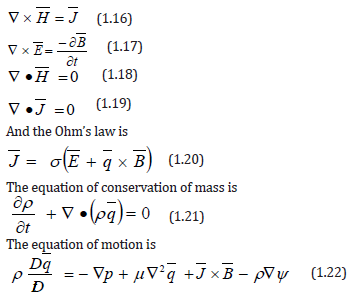
Where ψ is the gravitational potential?
Magnetic diffusion equation is
figure :
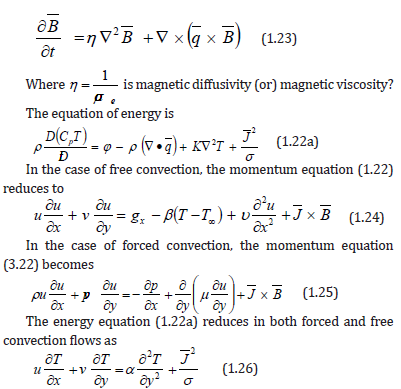
Non-Dismensionalisation
We introduce the following dimensionless parameters
figure :
Also
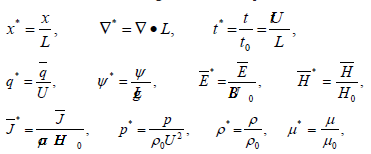
By using the above dimensionless parameters, the equations (1.16) to (1.23) after dropping the asterisks are
figure :
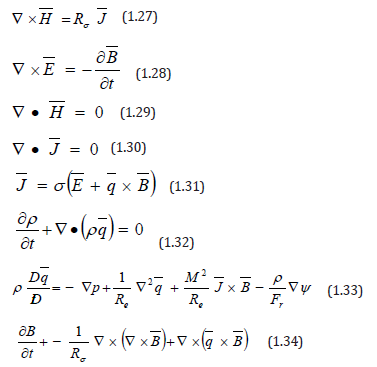
The dimensionless parameters appearing in the above equations are
a. Re = Reynolds number =
figure :
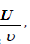
which is measure of the ratio of inertial to viscous forces.
b. Rσ = magnetic Reynolds number =
figure :
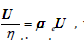
which is a measure of the ratio of magnetic convection to magnetic diffusion. A small Rσ(R<< 1) indicates that the induced magnetic field is small compared to the total or the applied magnetic field.
figure :
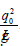
which is a measure of the ratio if inertial force to the gravitational force.
figure :
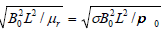
figure :
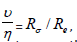
which is a measure of the ratio of vorticity diffusion to magnetic diffusion. This number is usually very small, so that the magnetic field diffuses much more easily than the vorticity.
Magneto Hydrodynamic Thermal Convection
MHD Convection equations
The following are the non-dimensional equations governing MHD convection flows:
figure :
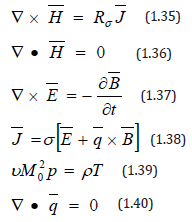
We non-dimensional the momentum and energy equations (1.24), (1.25) and (1.26) using the dimensionless parameters defined in 6. The dimensionless form of the momentum and energy equations are
figure :
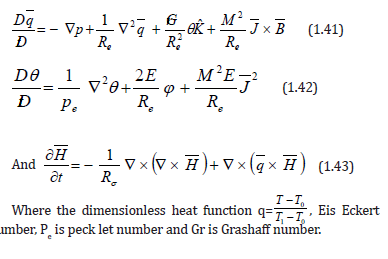
References
- Devika B, Satya Narayana PV, Venkataramana S (2013) MHD oscillatory flow of a visco elastic fluid in a porous channel with chemical reaction. International Journal of Engineering Science Invention 2(2): 26-35.
- Raju MC, Varma SVK, Seshaiah B (2014) Heat transfer effects on a viscous dissipative fluid flow past a vertical plate in the presence of induced magnetic field. Ain Shams Engineering Journal 5: 1361-1369.
- Ravikumar V, Raju MC, Raju GSS (2014) Combined effects of heat absorption and MHD on convective Rivlin-Ericksen flow past asemiinfinite vertical porous plate with variable temperature and suction. Ain Shams Engineering Journal 5(3): 867-875.
- Raju KVS, Sudhakar Reddy T, Raju MC, Satya Narayana PV, Venkataramana S (2014) MHD convective flow through porous medium in a horizontal channel with insulated and impermeable bottom wall in the presence of viscous dissipation and Joule heating. Ain Shams Engineering Journal 5(2): 543-551.
- Hari Priya G, Bhuvana Vijaya R, Siva Prasad R (2015) Hall current effects on steady hydro magnetic rotating flow of a viscous incompressible fluid through a porous medium in a parallel plate channel with radiative heat transfer. Quest Journals Journal of Research in Applied Mathematics 2(2): 1-11.
- Swetha Ravi, Jagdish Prakash, Viswanatha Reddy G, Vijaya Kumar Varma S (2015) Effects of thermal radiation and radiation absorption on flow past an impulsively started infinite vertical plate with newtonian heating and chemical reaction. Open Journal of Fluid Dynamics 5: 364-379.
- Misra JC, Adhikary SD (2016) MHD oscillatory channel flow, heat and mass transfer in a physiological fluid in presence of chemical reaction. Alexandria Engineering Journal 55(1): 287-297.
- Ramaiah P, Vijay Kumar Varma S, Rama Krishna Prasad K, Balamurug KS (2016) An chemical reaction and radiation absorbtion effects on MHD convective heat and mass transfer flow of a viscoelastic fluid past an oscillating porous plate with heat generation absorption. Int J Chem Sci 14(2): 570-584.
- Joseph KM, Magaji AS, Peter A, Tijani NZ (2016) Effect of variable suction on unsteady MHD oscillatory flow of jeffrey fluid in a horizontal channel with heat and mass transfer. Journal of Scientific and Engineering Research 3(3): 599-610.
- Maruf Hasan, Enamul Karim, Abdus Samad (2017) MHD free convection flow past an inclined stretching sheet with considering viscous dissipation and radiation. Open Journal of Fluid Dynamics 7: 152-168.
- Falade JA, Ukaegbu JC, Egere AC, Samuel OA (2017) MHD oscillatory flow through a porous channel saturated with porous medium. Alexandria Engineering Journal 56(1): 147-152.
© 2018 Raju MC. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version