Merging Generalizability Theory and Bifactor Modeling to Improve Psychological Assessments

Generalizability theory and bifactor models continue to play significant roles in representing psychometric properties of scores from measures within a wide variety of disciplines, including psychology and psychotherapy. Emanating from the seminal work of Cronbach and colleagues in the 1960s and 70s [1,2], generalizability theory has revolutionized measurement practice beyond traditional classical test theory techniques by creating an all-encompassing framework for both objectively and subjectively scored measures that explicitly identifies the domains to which results are generalized, allows for separation of multiple sources of measurement error, and provides straightforward procedures for estimating the effects of changes made to measurement procedures. Bifactor models first appeared in research literature over 85 years ago [3,4], but only within the last decade or so have applications of such models truly begun to proliferate [5]. Bifactor models extend partitioning of explained variance (i.e., universe score variance in generalizability theory, true score variance in classical test theory, and communality in factor analyses) into general and group factor effects to provide further insights into score dimensionality and possible benefits gained when reporting subscale in addition to composite scores. Within a bifactor model, interrelationships among item scores are accounted for by a general factor reflecting common variance across all items and by additional group factors reflecting unrelated unique variance shared among non-overlapping clusters of items with similar content.

Popularity of generalizability theory and bifactor modeling

To gauge interest in use of generalizability theory and bifactor models within the last five years alone, we recorded 568 hits using the keywords “generalizability theory” and 999 hits using the keywords “bifactor model” in separate PsycNet database searches between the years 2018 and 2022. Although rarely applied in the same study, generalizability theory and bifactor modeling techniques have been used individually in many common domains, including psychology, health sciences, education, and athletics. Part of the reason why such studies seldom overlap is that generalizability theory is typically represented within Analysis of Variance (ANOVA) frameworks and bifactor analyses within factor analytic frameworks. However, researchers have recently demonstrated that both frameworks can be integrated into structural equation models to take advantage of their joint benefits [6-10].

An example of generalizability theory-based bifactor designs and their application

Although it is beyond the scope of this brief article to describe the merger of generalizability theory and bifactor modeling in detail, we provide one example of combining them in Table 1 using Negative-Emotionality domain and facet scores (Anxiety, Depression, and Emotional Volatility) from the recently expanded form of the Big Five Inventory [11]. The Negative-Emotionality composite scale has 12 items, each nested facet subscale has 4 items and items within all scales are equally balanced for positive and negative wording to reduce possible effects of acquiescence response bias. Analyses discussed here are based on responses from 389 college students, who provided informed consent before completing the BFI-2 on multiple occasions for an ongoing research study that was preapproved by the university’s Institutional Review Board (ID# 200809738).

Table 1:Partitioning of variance and value-added ratios for negative emotionality scales.

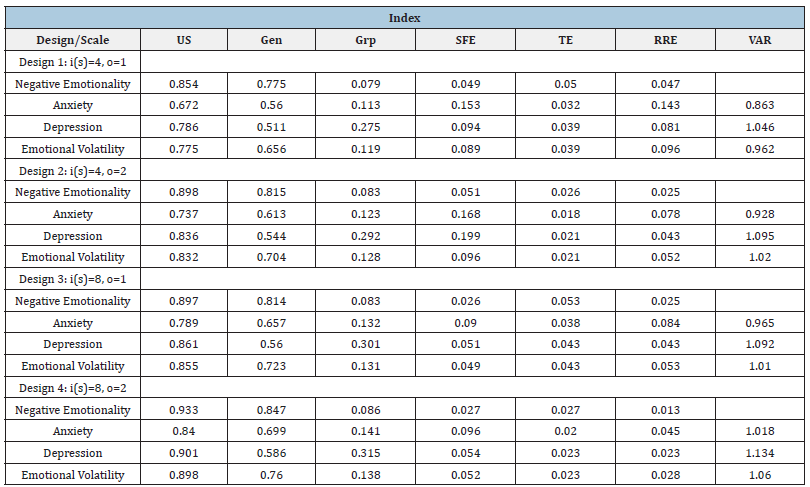
Note: i(s) = number of items within each subscale, o = number of occasions, US = proportion of universe score variance (also called a generalizability coefficient in applications of generalizability theory), Gen = proportion of general factor variance, Grp = proportion of group factor variance, SFE = proportion of specific-factor error, TE = proportion of transient error, RRE = proportion of random-response error, and VAR = value-added ratio.

Partitioning of variance

In Table 1, we summarize results for four persons × items × occasions random effects generalizability theory designs. Scales are considered fixed within the designs because results are not generalized beyond the constructs they represent, whereas sampled items and occasions are considered exchangeable with other items and occasions drawn from broader universes. Results in Table 1 represent partitioning of variance for BFI-2 Negative Emotionality composite and subscale scores, first assuming that the scales are administered in their original form (4 items per subscale) on one occasion (Design 1), and then doubling numbers of items and/ or occasions (Designs 2-4). Indices in Table 1 for partitioning of variance reflect proportions of observed score variance accounted for universe scores (i.e., general plus group factor effects), general factor effects, group factor effects, and three sources of measurement error (specific-factor, transient, and random-response). Specificfactor error represents person-specific idiosyncratic reactions to item content and response options such as understandings or misunderstandings of words that endure across occasions but are unrelated to the constructs being measured.

Transient error represents independent person-specific effects within the administration setting stemming from respondent dispositions, mindsets, and physiological conditions; reactions to administration and environmental factors; and other entities that temporarily affect behavior within that setting. Random-response error reflects additional momentary “within-occasion noise” effects that follow no systematic pattern (e.g., distractions, lapses in attention, etc.); [12-14]. Within other paradigms such as latent state-trait theory, specific-factor and transient error are often respectively described as method and state effects [15-17].

Results in Table 1 reveal that universe scores account for the majority of observed score variance across all scales and designs, with general factor effects (i.e., the global construct Negative Emotionality) accounting for most of that variance. Across the three subscales, Depression shows the strongest unique (group) effects, followed respectively by Emotional Volatility and Anxiety. As numbers of items or occasions increase, proportions of universe score, general factor, and group factor effects increase, but the ratios of general to group factor variance remain the same. Within the baseline design (Design 1), each source of measurement error accounts for noteworthy proportions of observed score variance, ranging from 0.049 to 0.153 for specific-factor error, 0.032 to 0.050 for transient error, and 0.047 to 0.143 for random-response error. Further increases in numbers of items decreases proportions of specific-factor and random-response error, whereas increases in numbers of occasions decreases proportions of transient and random-response error. Consequently, increasing items would best reduce specific-factor (method) error, increasing occasions would best reduce transient (state) error, and increasing either items or occasions would reduce random-response error. When using results like those shown in Table 1, users and developers of assessment measures would typically first consider minimally acceptable proportions of universe score variance (e.g., often 0.80) for each scale, then determine combinations of numbers of items and occasions that would meet those criteria, and finally select the combination that is easiest to implement in practice.

Subscale added value

In the last column in Table 1, we present value-added ratios [18] that can be used to determine possible benefits gained by reporting subscale in addition to composite scores. A VAR is a rescaling of indices described by Haberman [19] to determine whether a subscale’s observed scores better represent that subscale’s true or universe scores than would the corresponding composite scale’s observed scores. In general, subscale added value is increasingly supported as VARs deviate upwardly from 1.00. Within the designs shown in Table 1, the Depression subscale meets the criterion for added value for the baseline design with four items per subscale and one occasion and all subsequent designs with added items and/or occasions; the Emotional Volatility subscale meets the criterion for all but the baseline model; and the Anxiety subscale requires at least eight items per subscale and two occasions to meet the criterion. These results indicate that the Depression subscale provides added value beyond the composite scale in all instances but that increases in items, occasions, or both would be required for the Emotional Volatility and Anxiety subscales to do so. Such findings underscore benefits of generalizability theory-based bifactor analyses in isolating conditions under which some or all subscales would be expected to contribute meaningful information beyond composites in practical applications.

We hope that this brief excursion into generalizability theory and bifactor model designs piques readers’ interest in applying these techniques when measuring constructs relevant to psychology and psychotherapy. Many additional extensions of these procedures are explained in detail in recent articles that also include instruction and computer code for analyzing a wide variety of generalizability theory-based bifactor designs [6-10]. We encourage readers to explore uses of these methods for developing, evaluating, and improving assessment procedures not only within general psychological and psychotherapeutic contexts, but also within any discipline for which generalizability theory and bifactor techniques can be meaningfully combined.

1. Cronbach LJ, Rajaratnam N, Gleser GC (1963) Theory of generalizability: A liberalization of reliability theory. British Journal of Statistical Psychology 16(2): 137-163.
2. Cronbach LJ, Gleser GC, Nanda H, Rajaratnam N (1972) The dependability of behavioral measurements: Theory of generalizability for scores and profiles. American Educational Research Journal 11(1).
3. Holzinger KJ, Swineford F (1937) The bi-factor method. Psychometrika 2: 41-54.
4. Holzinger K J, Harman HH (1938) Comparison of two factorial analyses. Psychometrika 3: 45-60.
5. Reise SP (2012) The rediscovery of bifactor measurement models. Multivariate Behavioral Research 47(5): 667-696.
6. Vispoel WP, Hong H, Lee H (2023) Benefits of doing generalizability theory analyses within structural equation modeling frameworks: Illustrations using the Rosenberg self-esteem scale. Structural Equation Modeling: A Multidisciplinary Journal.
7. Vispoel WP, Lee H, Chen T, Hong H (2023) Extending applications of generalizability theory-based bifactor model designs.
8. Vispoel WP, Lee H, Hong H, Chen T (2023) Analyzing and comparing univariate, multivariate, and bifactor generalizability theory designs for hierarchically structured personality traits.
9. Vispoel WP, Lee H, Xu G, Hong H (2022) Integrating bifactor models into a generalizability theory structural equation modeling framework. Journal of Experimental Education.
10. Vispoel WP, Lee H, Xu G, Hong H (2022) Expanding bifactor models of psychological traits to account for multiple sources of measurement error. Psychological Assessment 32(12): 1093-1111.
11. Soto CJ, John OP (2017) The next Big Five Inventory (BFI-2): Developing and accessing a hierarchical model with 15 facets to enhance bandwidth, fidelity, and predictive power. Journal of Personality and Social Psychology 113(1): 117-143.
12. Le H, Schmidt FL, Putka DJ (2009) The multifaceted nature of measurement artifacts and its implications for estimating construct-level relationships. Organizational Research Methods 12(1): 165-200.
13. Thorndike RL (1951) Reliability. In: Lindquist EF (Ed.), Educational Measurement, American Council on Education, Washington DC, USA, pp. 560-620.
14. Schmidt FL, Le H, Ilies R (2003) Beyond alpha: An empirical investigation of the effects of different sources of measurement error on reliability estimates for measures of individual differences constructs. Psychological Methods 8(2): 206-224.
15. Geiser C, Lockhart G (2012) A comparison of four approaches to account for method effects in latent state-trait analyses. Psychological Methods 17(2): 255-283.
16. Steyer R, Ferring D, Schmitt MJ (1992) States and traits in psychological assessment. European Journal of Psychological Assessment 8(2): 79-98.
17. Vispoel WP, Xu G, Schneider WS (2022) Interrelationships between latent state-trait theory and generalizability theory in a structural equation modeling framework. Psychological Methods 27(5): 773-803.
18. Feinberg RA, Wainer H (2014) A simple equation to predict a sub score’s value. Educational Measurement: Issues and Practice 33(3): 55-56.
19. Haberman SJ (2008) When can sub scores have value? Journal of Educational and Behavioral Statistics 33(2): 204-229.