Association between Multiple Sclerosis and Cardiovascular Dysfunction

Introduction

Multiple Sclerosis (MS) is a chronic neurological disorder, associated with inflammation and demyelination of the central nervous system with frequent relapsing-remitting episodes and axonal degeneration leading to irreversible progressive invalidity. MS may affect cardiovascular functions in different ways leading to problems of heart rhythm and rate, left ventricular systolic function, pulmonary edema or cardiomyopathy, etc. and also by brainstem lesions affecting autonomic pathways in the medulla, overall plaque burden and thus increases risk of Cardiovascular Disease (CVD) [1]. Considering Composite Autonomic Scoring Scale (CASS) and Heart Rate Variability (HRV) [2] found significantly higher burden of autonomic dysfunction among patients with Primary Progressive MS (pwPMS) than patients with relapsing-remitting MS (pwRRMS), which was particularly evident for sweating dysfunction. The occurrence of CVD were observed among patients with MS and existence of association between them [3,4]. Genetic liability to MS was found to be associated with increased risks of Coronary Artery Disease (CAD), Myocardial Infarction (MI), Heart Failure (HF), stroke, but not with Atrial fibrillation or other stroke subtypes (Large Artery Stroke (LAS), Cardioembolic Stroke (CES), and Small Vessel Stroke (SVS) [5]. Controversial results emerged on risk of occurrence of CVD and death among MS patients [6]. However, the cause and effect relationship between MS and CVD are not exactly known [7].

Association between MS and CVD can be approached using biomarkers, genetical configurations or by scales to assess MS and CVD. Instruments to measure functional deficits of MS patients with Coronary Heart Disease (CHD) consider items which differ in item formats, dimensions, scoring systems, etc. and are not comparable. Scores of such scales suffer from methodological shortcomings. The paper describes limitations of scales measuring MS and CVD and provides assumption-free method to convert ordinal item scores to proposed scores following normal distribution, satisfying desired properties for better comparisons, measurement of association, facilitating identification of areas requiring changes in clinical practice, treatment protocols, community program management and estimating population parameters and testing of statistical hypothesis.

Literature survey

Autonomic Symptom Profile (ASP) with 169 items in 11 dimensions of autonomic function provides clinically relevant scores of autonomic symptom severity and distribution of symptoms. The scale was validated with the Composite Autonomic Symptom Score (COMPASS) containing 72 items distributed in 11 dimensions and an additional 12 items to generate two validity scores [8]. Major limitations are:
A. The highly complicated scoring system of COMPASS involves computer analysis to generate scores which may be inconsistent.
B. ASP is time consuming even if it is shortened to items relevant for COMPASS.
C. Some COMPASS items are less meaningful or redundant for scoring severity of autonomic functions and symptoms.
D. Significant overlapping of COMPASS dimensions like syncope with orthostatic.
E. The relevance of reflex syncope for assessment of autonomic deficits is not beyond questions.

The instrument was redesigned to a simplified version [8] known as COMPASS 31 containing binary items for presence (1) or absence of the symptom (0); 4-point items for time course of a symptom (0 to 3); 3-point items for frequency of symptoms (0 to 2), severity of symptoms (1 to 3), changes in bodily functions (0 to 2). COMPASS 31 has been used to evaluate autonomic dysfunction in people with systemic sclerosis [9] and other diseases like Parkinsonism, Fibromyalgia (FM) and small-fiber polyneuropathy. Popular HRV analysis to detect Cardiovascular Autonomic Neuropathy (CAN) through electrocardiography recordings [10] was preferred over traditional CARTs since HRV is more sensitive and accurate [11]. A too simplistic framework to link HRV frequency components (LF and HF) with the sympathetic and parasympathetic autonomic nervous system is the major limitation of HRV [12]. Positive correlation was found between the questionnaire measuring FM severity (FIQ) and COMPASS [13] implying that autonomic dysfunction is inherent to FM. Cohort study by [14] covering people with MS and without MS (matched control) found that MS is associated with an increased risk of CVDs, which cannot be explained by traditional vascular risk factors.

Other MS scales (Illustrative)

20-point Expanded Disability Status Scale (EDSS) with binary, 5-point and 6-point items measures disability, functions of CNS and progression of MS, where score ranges from zero (indicating “Normal”) to 10 (death by MS) with 0.5 point steps combining eight Functional System (FS) [15]. EDSS with two modes (bimodal) has been criticized for its limitations [16]. Based on changes in assessment [17], proposed calculation of brain functions FS in EDSS by EDSS_Basal and EDSS_Modified using the scores from the Brief International Cognitive Assessment for MS (BICAMS) [18]. But EDSS_Basal and EDSS_Modified follow different distributions and comparison of means by t-statistics, assuming normally distributed scores is unjustified.

Guy’s Neurological Disability Scale (GNDS) with 12 functional dimensions is obtained by adding dimension scores, each ranging between 0 to 5 assuming equal importance to the dimensions. Here, a higher score implies more disability [19]. Suggestions of Neuro status by modifying gait assessment criteria and including new definitions of each FS by [20] does not propose a single test or homogeneous assessment criteria. A single clinical outcome measure of sustained disease progression, failing which an integration of outcome measures reflecting various stages of MS, was preferred [21].

CVD-specific instruments

Seattle Angina Questionnaire (SAQ): Aims at measuring FS of CAD patients. SAQ with 19 items on five clinically relevant dimensions: physical limitation, anginal stability, anginal frequency, treatment satisfaction and disease perception/quality of life is often used as a HRQoL instrument because seven of its 19 items relate to emotional health. However, SAQ does not provide a single summary score of a patient reflecting overall assessment of patients’ health status. A shortened version SAQ-7 with 7 number of 6-point items was derived with provision of single summary score [22]. Diary reports were preferred over SAQ [23].

Minnesota Living with Heart Failure (MLHF) questionnaire:Contains 21 items; each in 6-point scale (0 to 5) where 0≤Total score≤105. It provides scores for two dimensions, physical and emotional, and a total score (assuming one-dimensionality). Researchers differed in the factor structure of MLHF. The existence of the third factor was confirmed [24].

Myocardial Infarction Dimensional Assessment Scale (MIDAS):The 35 items of MIDAS questionnaire are arranged in hierarchy order to assess seven dimensions, is designed specifically for patients with angina, MI or heart failure [25]. Each dimension is scored separately using Mokken Scaling Procedure, a computer program on the basis of a range of diagnostic criteria.

Cardiovascular Limitations and Symptoms Profile (CALP):Involves 37 items, four symptoms subscales and five functional limitation subscales [26]. Each subscale contains four to six items and scores are weighted to provide a total for each subscale.

Observations

Major disadvantages of summative scale scores are:
A. Addition of item scores and dimension scores are not meaningful due to non-satisfaction of equidistant property, assigning equal importance to the items/dimensions despite different contributions of items/dimensions to total score, different correlations between item/dimension and total score, different factor loadings, etc.
B. Unknown and different distributions of item scores creates problems in interpreting and finding distribution of X±Y and further use of X±Y
C. Avoid zero scores. Score 0-1 items as say 1-2.
D. Fails to generate normally distributed scale scores, which is the basic assumption of analysis like t-test, Analysis of Variance (AVOVA), Principal Component Analysis (PCA), Factor Analysis (FA), estimation and testing of population parameters, etc.

Remedial actions on shortcomings of various scales on MS and CVD

a) Follow the convention higher score ⇔ better health status to ensure same score direction. This may require inverse scoring of items that do not follow the convention.
b) Transform positive ordinal item scores to continuous, monotonic scores following Normal distribution in a fixed score range (say 1 to 100). Find dimension scores and scale scores as sum of the normally distributed item scores so that distributions of dimension/scale scores are also normal.
c) Normally distributed scale scores satisfy desired properties to undertake parametric analysis and also help to improve Receiver Operating Characteristic (ROC) curve and Area Under The Curve (AUC) analysis [27].

Measures of association

Frequency based approach:Choose a suitable test of MS and another test for CVD where outcomes of each test is dichotomous, either positive or negative or high and low severity. Association between two outcome variables may be arrived using 2×2 contingency table as follows (Table 1): Associations considering cell frequencies of contingency table are: a. Chi-square measure of association

distribution with (r-1)(s-1) degrees of freedom for r-rows and s-columns of r×s contingency table. Here, fexpected for the (i–j)-th cell is

test is that the two diseases are independent; that is, the level of MS does not predict the level of CVD.
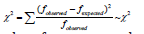
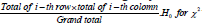
b. Pearson’s Contingency Coefficient(C) is a measure of the relative (strength) of association between two variables and given by

where N is the sample size. C can be used for incidence and also prevalence studies but may not be applicable for paired data.
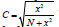
C. Cramer’s V-Coefficient: x2 may get increased for large N, even if the variables may not have any substantive relationship. Cramer’s V-Coefficient helps to improve association by

where q = minimum (r, c) and 0≤V≤1

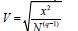
Table 1:Contingency table-clinical evidences and tests.

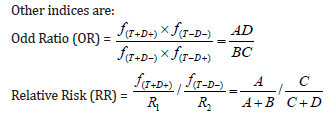
RR is usually calculated for cohort studies where patients with and without exposure (say MS) are followed for particular outcome (say CVD). RR=1⟹ incidence is the same among those exposed and unexposed. OR is calculated for case-control or cross-sectional studies and is interpreted in line with RR. OR=1⟹ no association exists. OR<⟹ exposure is protective i.e. exposure is less likely among the case group, and OR> 1⟹ exposure is a risk factor i.e. exposure is less likely among the control group. Both RR and IR fail if the assumption of independence is violated. Confidence intervals of both OR and RR can be formed to reflect range of uncertainty.

Measures of association based on contingency table need to find meaningful scale scores to obtain frequency of True positive, false positive, false negative and true negative. One solution is through equivalent score combinations {X₀,Y₀} defined as

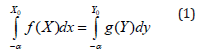
where the score X0 in a scale (MS) with density function f(X) is equivalent to the score Y₀ in another scale (say CVD) with density function g(Y) i.e. area under f(X) up to X₀=area under g(Y) up to Y₀. Normally distributed scores of MS and CVD help to solve (1) and find equivalent scores Y₀ of CVD for a given score X₀ of MS or vice versa by solving (1) using standard Normal table [28]. If X₀ is the cut-off score for MS (people with scores ≥X₀ are suffering from MS and people with score < X₀ are MS-negative), with equivalent score Y0 of CVD, then

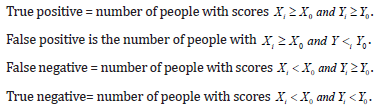
Such classification of the sample avoids subjectivity in deciding cell frequencies of 2×2 contingency table. A cut-off score X0 may be decided by ROC curve. ROC curve was generated for each validated miRNA, and AUC for MS versus Healthy Control group [29]. However, parametric method may result in improper ROC curve if data violate the assumptions of normality and similar within-group variances.

Other measures of association

Spearman ρ based on ranks of individuals in two tests fails when data show grouped frequency distributions. Accuracy of Spearman ρ is much less than correlation coefficient between scores of two scales (rXY) measuring two diseases. Measures based on correlation are preferred over frequency based measures and Spearman ρ. However, high correlation may not imply linearity between two variables. For example, if X takes integer values from 1 to 30, rx,x² = 0.97. Thus, linear regression Y=α+βX needs to test normality of error scores and test H0:S²_E=0 to ensure linearity. In addition, homogeneity of data on X or Y or both can lower value of rXY. Violation of assumptions of correlation may lead to biased, inconsistent and invalid estimates [30]. Effect sizes, which indicate the magnitude of the difference between groups (by t-test), measures of variability (by F-test), etc. are more informative when interpreting epidemiologic data [31]. Such tests assume normally distributed data.

Converting ordinal data to follow Normal distribution

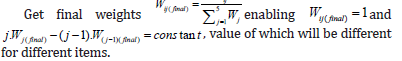
Observations

A. W_j(Final) are based on empirical probabilities. B. If f_ij=0 for a particular j-th level of an item, this can be taken as zero value for scoring k-point items as weighted sum. C. Equidistant scores (E) as weighted sum are continuous implying better admissibility of arithmetic aggregation. E-scores or linear transformations of E-scores facilitate addition with bio-markers (usually in ratio or interval scales) Standardize E-scores by

Convert the Z-scores to proposed P-scores by

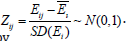
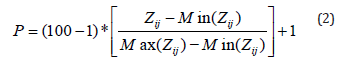
For the i-th item, P_i~N (μ_i,σ_i²) and 1≤Pi≤100.μ_i and σ_i² canbe estimated from the data. P-score of an item can be obtained irrespective of number of items and number of response-categories in items. Pathological data could be binary or categorical or in ratio scales. Binary and categorical data may be transformed to follow normal by the above said method and ratio scale data may be standardized followed by transformation (2) and added. The dimension score of an individual is sum of P-scores of relevant items. Scale score is similarly taken as sum of domain scores or P-scores of all items.

Properties

Dimension scores (Di) and scale scores (Si) of the i-th individual are continuous, monotonic, normally distributed with better admissibility of arithmetic aggregation. They facilitate parametric analysis including estimation of population mean (μ), population variance (σ²), confidence interval of μ, testing hypothesis like H0: μ₁=μ₂ or H₀: σ₁²=σ₂² etc. either for longitudinal data or snap-shot data. Same range of item-wise P-scores avoids variation due to different score-ranges. However, variance of dimension scores may vary depending on the number of items in dimensions. The dimensions can be ranked based on elasticity, defined

Percentage progress/deterioration of the i-th person during successive time-periods is given by

, reflecting responsiveness of the scale and also effectiveness of a treatment plan. S_i(t)-S_i(t-1)>0 implies progress in t-th period over (t-1)-th period. The reverse is true for S_i(t)-S_i(t-1)>0 . Deterioration in terms of scale scores may be probed to identify dimension(s) showing deterioration for possible corrective actions or treatment plan/care.

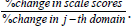
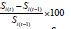
Progress for a group of persons is reflected if (t ) (t 1) S S− > . Normality of Si helps to test H0: μSt = μS(t-1). Significance of responsiveness of a scale in terms of

can be tested since ratio of two normally distributed variables follows χ2 distribution.

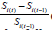
Testing of significance of progress i.e. testing H0: Progress(t+1)over t=0 may avoid need to find minimal important difference of a scale for comparing changes over time among the group of patients. Plotting of progress of a patient or a group of patients across time can be used to compare progress pattern i.e. response to treatments from the start.

Discussion

Limitations of scales to assess MS or CVD may be avoided by the proposed transformations. Binary and categorical pathological data may be transformed to follow normal by such transformations. Ratio scale data may be standardized followed by transformation (2). Such transformed data facilitate meaningful addition. Dimension score (D_X) is sum of P-scores of relevant items following normal where parameters are derived from the data. Scale score (S_X) is similarly taken as sum of domain scores or P-scores of all items.

Measures of association based on contingency table need to find meaningful scale scores to obtain frequency of True positive, False positive, False negative and True negative. Proposed SX following Normal distribution help in meaningful aggregation of item scores and help in classification of the sample avoiding subjectivity in deciding cell frequencies of 2×2. Contingency table, where cut-off score for diagnosis may be decided by ROC curve. In addition, proposed scores facilitate parametric analysis including estimation of population parameters like mean (μ), variance (σ²), confidence interval of μ, testing hypothesis like H₀: μ₁=μ₂ or H₀: σ₁²=σ₂² etc. either for longitudinal data or snap-shot data, ranking of dimensions based on elasticity, etc. Association between MS and CVD in terms of correlations is preferred over frequency based measures. However, correlations may not imply linearity.

Conclusion

The proposed method generating normally distributed scores contributes to improve scoring of instruments. It is suggested to convert ordinal item scores to normally distributed scores which help in better comparisons, ranking, assessing associations among scales. Future empirical investigations are proposed with multi data sets to find associations including ROC–AUC analysis with normally distributed data..

References

1. Kaplan Tamara B, Berkowitz Aaron L, Samuels Martin A (2015) Cardiovascular dysfunction in multiple sclerosis. The Neurologist 20(6): 108-114.
2. Adamec Ivan, Crnošija Luka, Junaković Anamari, Skoric MK, Hebek M (2018) Progressive multiple sclerosis patients have a higher burden of autonomic dysfunction compared to relapsing remitting phenotype. Clinical Neurophysiology 129(8): 1588-1594.
3. Jadidi E, Mohammadi M, Moradi T (2013) High risk of cardiovascular diseases after diagnosis of multiple sclerosis. Mult Scler 19(10):1336-1340.
4. Jakimovski D, Guan Y, Ramanathan M, Guttman BW, Zivadinov R (2019) Lifestyle-based modifiable risk factors in multiple sclerosis: Review of experimental and clinical findings. Neurodegener Dis Manag 9(3):149-172.
5. Yang F, Hu T, He K, Ying J, Cui H (2022) Multiple sclerosis and the risk of cardiovascular diseases: A mendelian randomization study. Front Immunol 13: 861885.
6. Wenz I, Dalgas U, Stenager E, Eijnde BO (2013) Risk factors related to cardiovascular diseases and the metabolic syndrome in multiple sclerosis-a systematic review. Mult Scler 19(12): 1556-1564.
7. Mincu RI, Magda LS, Florescu M, Velcea A, Mihaila S, et al. (2015) Cardiovascular dysfunction in multiple sclerosis. Maedica (Bucur) 10(4): 364-370.
8. Sletten DM, Suarez GA, Low PA, Mandrekar J, Singer W, et al. (2012) COMPASS 31: A refined and abbreviated composite autonomic symptom score. Mayo Clin Proc 87(12): 1196-1201.
9. Adler BL, Russell JW, Hummers LK. McMahan Z (2018) Symptoms of autonomic dysfunction in systemic sclerosis assessed by the COMPASS-31 questionnaire. The Journal of Rheumatology 45(8): 1145-1152.
10. Kang JH, Kim JK, Hong SH, Lee CH, Choi BY (2016) Heart rate variability for quantification of autonomic dysfunction in fibromyalgia, Annals of Rehabilitation Medicine 40(2): 301-309.
11. Vinik AI, Ziegler D (2007) Diabetic cardiovascular autonomic neuropathy. Circulation 115(3): 387-397.
12. Hayano J, Yuda E (2019) Pitfalls of assessment of autonomic function by heart rate variability. J Physiol Anthropol 38(1): 1.
13. Solano Carla, Martinez, A, Becerril L, Vargas A, Figueroa J, et al. (2009) Autonomic Dysfunction in Fibromyalgia Assessed by the Composite Autonomic Symptoms Scale (COMPASS). Journal of Clinical Rheumatology 15(4): 172-176.
14. Palladino R, Marrie RA, Majeed A, Chataway J (2020) Evaluating the risk of macrovascular events and mortality among People with multiple sclerosis in England. JAMA Neurol 77(7): 820-828.
15. Kurtzke JF (1983) Rating neurologic impairment in multiple sclerosis: An Expanded Disability Status Scale (EDSS). Neurology 33(11): 1444-1452.
16. Goodkin DE, Cookfair D, Wende K, Bourdette D, Pullicino P, et al. (1992) Inter-and intrarater scoring agreement using grades 1.0 to 3.5 of the Kurtzke Expanded Disability Status Scale (EDSS). Multiple sclerosis collaborative research group. Neurology 42(4): 859-863.
17. Saccà F, Costabile T, Carotenuto A, Lanzillo R, Moccia M, et al. (2017) The EDSS integration with the brief international cognitive assessment for multiple sclerosis and orientation tests. Mult Scler 23(9): 1289-1296.
18. Artemiadis A, Bakirtzis C, Chatzittofis A, Christodoulides C, Nikolaou G, et al. (2021) Brief International Cognitive Assessment For Multiple Sclerosis (BICAMS) cut-off scores for detecting cognitive impairment in multiple sclerosis. Mult Scler Relat Disord 49: 102751.
19. Sharrack B, Hughes RA (1999) The Guy's Neurological Disability Scale (GNDS): A new disability measure for multiple sclerosis. Multiple Sclerosis Journal 5(4): 223-233.
20. Kappos L, D’Souza M, Lechner-Scott J, Lienert C (2015) On the origin of neurostatus. Mult Scler Relat Disord 4(3):182-185.
21. Goldman MD, Motl RW, Rudick RA (2010) Possible clinical outcome measures for clinical trials in patients with multiple sclerosis. Ther Adv Neurol Disord 3(4): 229-239.
22. Chan Paul, Chan S, Jones PG, Arnold SA (2014) Development and validation of a short version of the seattle angina questionnaire. Circulation Cardiovascular Quality and Outcomes 7(5): 640-647.
23. Arnold SV, Kosiborod M, Li Y, Jones PG, Yue P, et al. (2014) Comparison of the seattle angina questionnaire with daily angina diary in the TERISA clinical trial. Circulation: Cardiovascular Quality and Outcomes 7(6): 844-850.
24. Bilbao A, Escobar A, García-Perez L, Navarro G, Quiros R (2016) The Minnesota living with heart failure questionnaire: Comparison of different factor structures. Health Qual Life Outcomes 14: 23.
25. Thompson DR, Jenkinson C, Roebuck A, Lewin RJP, Boyle RM, et al. (2002) Development and validation of a short measure of health status for individuals with acute myocardial infarction: The Myocardial Infarction Dimensional Assessment Scale (MIDAS). Qual Life Res 11(6): 535-543.
26. Lewin RJP, Thompson DR, Martin CR, Stuckey N, Devlen J, et al. (2002) Validation of the Cardiovascular Limitations and Symptoms Profile (CLASP) in chronic stable angina. J Cardiopulm Rehabi 22(3): 184-191.
27. Chakrabartty SN (2023) Screening and diagnostic tests for health-related quality of life. Global Health Science Journal 3(1).
28. Chakrabartty, Satyendra Nath (2021) Integration of various scales for measurement of insomnia. Research Methods in Medicine & Health Sciences 2(3): 102-111.
29. Nuzziello N, Vilardo L, Pelucchi P, Consiglio A, Liuni S, et al. (2018) Investigating the role of microRNA and transcription factor co-regulatory networks in multiple sclerosis pathogenesis. Int J Mol Sci 19(11): 3652.
30. Williams MN, Grajales CAGG, Kurkiewicz D (2013) Assumptions of multiple regression: Correcting two misconceptions. Practical Assessment 18(11): 1-14.
31. Greenland S, Senn SJ, Rothman KJ, Carlin JB, Poole C, et al. (2016) Statistical tests, P values, confidence intervals and power: A guide to misinterpretations. Eur J Epidemiol 31(4): 337-350.