Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System: A Metacognitive Intervention Study for Ineffective Mathematics Learners

The concept of “metacognition” was first proposed by Flavell J [1], who asserted that metacognition encompassed two main meanings. On the one hand, it includes knowledge of the individual’s own cognitive processes and cognitive outcomes, as well as knowledge of other related things. On the other hand, it refers to the active monitoring and regulation of one’s cognitive processes to achieve a certain goal or accomplish a certain task. Metacognition is observed to be involved in the regulatory process of thinking, which is the basis for the cognitive construction of critical thinking [2] and an important predictor of creative thinking ability [3], thereby playing an important role in human cognitive activity and thinking. Mathematics is a subject that focuses on thinking skills, which are of great significance to the development of students’ thinking, enhancement of their sense of application and innovation, and improvement of their learning ability, especially in junior high school when students are developing physically and mentally at a rapid rate. Good mathematical metacognition can help students manage their efficiency while learning mathematics [4]. Studies have revealed that students’ metacognition in mathematics can effectively promote the development of mathematical achievement [5,6] and students with high levels of mathematical metacognition have higher mathematical learning efficiency [7].

Currently, there are some relatively mature scales of mathematical metacognition scales, with a representative one being the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System, independently developed by Guangming Wang and his team. Certified by the National Copyright Administration of the People’s Republic of China, the system can measure students’ mathematical metacognitive levels in batches, perform intelligent diagnoses of mathematical metacognition, and provide targeted and personalized improvement plans based on the diagnosis results. However, there is currently no research to verify the effectiveness of its mathematical metacognitive interventions for improvement. Therefore, this study aims to use the diagnostic results of the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System to provide mathematical metacognitive interventions for junior high school students with low learning efficiency and examine the effectiveness of the interventions for junior high school students with different academic levels in mathematics.

Pre-intervention: Diagnosing the level of mathematical metacognition

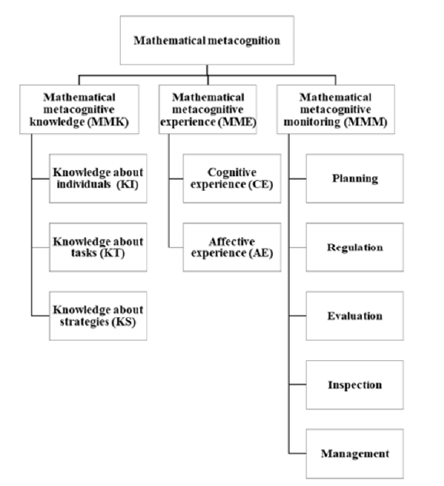
To improve students’ mathematical metacognition, we selected X middle school in Tianjin, China. The school has a strong faculty; however, in recent years, the insistence on test-free random admissions has led to a significant variation in students’ learning levels and abilities, and their academic performance has been lower compared with that of other schools, especially in the students’ poor learning efficiency in mathematics. To diagnose the overall mathematics metacognitive level of students, a stratified sampling method was used to select 92 students in grade 7 and 130 students in grade 8. With an effective rate of roughly 90.09%, 200 valid questionnaires were finally obtained (47% for boys and 53% for girls).To maintain consistency with the intelligent system, this paper used the mathematical metacognitive questionnaire for junior high school students developed by Guangming Wang et al. and conventional models [8], which divided mathematical metacognition into Mathematical Metacognitive Knowledge (MMK), Mathematical Metacognitive Experience (MME), and Mathematical Metacognitive Monitoring (MMM). The three domains were further divided into ten sub-dimensions (Figure1).

Figure 1: Dimensional structure of mathematical metacognition.

Intervention: Intervention guidance based on the intelligent improvement program

Based on the results of the systematic normative diagnosis, Class A, with the lowest level of mathematical metacognition, was selected for intervention as a whole. To make the results of the study more reliable, the students in Class A who did not take the pre-test were additionally evaluated before the intervention, and the mathematical metacognitive level of Class A was recalculated. The students’ mathematical metacognitive level was diagnosed and analyzed with the help of the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System. After importing the class data into the system, the results of the intelligent diagnosis were automatically output. These results included two aspects: the overall level of students’ mathematical metacognition and the intelligent perception of students’ mathematical metacognition weaknesses based on their scores in each dimension, with the output being targeted intelligent solutions for improvement.The system’s intelligent analysis revealed that the overall metacognition of Class A was at an average level (mean value of mathematical metacognition was 94.83, with a maximum score of 137 and a minimum score of 48, and a standard deviation of 20.68).

The lowest level of MME was found in the first-level dimension, and by comparing the data of sub-dimensions, the following descending order was obtained: management>KT>CE>regulatio n>planning>KI>AE>KS>inspection>evaluation. The percentiles of the last six dimensions were all below average, especially the evaluation dimension. Thus, it was determined that Class A needed improvement in mathematical metacognition.According to the intelligence improvement strategy, an intervention was implemented for about three months for all students in Class A. The intervention consisted of three stages. The first stage consisted of intensive lectures and case demonstrations in which knowledge of mathematical metacognition was explained to deepen its understanding. The intelligence diagnosis results were explained so students understood their individual mathematical metacognitive level, and the intelligence improvement strategy plan was interpreted to master the mathematical metacognition improvement strategies. The second stage involved individual instruction and teacher support to overcome the common problems of students to ensure the smooth implementation of the improvement strategy program and guide teachers to promote the effective implementation of the program. The third stage involved internalization by all parties and habit maintenance to maintain the frequency of supervision and guidance to form a class metacognitive guidance model that solidifies good learning habits.

Intervention results: Better mathematical metacognitive improvement in groups with high and ordinary scores

Based on the diagnostic results of the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System, after the intervention of Class A through the “three-stage, six-step” guidance model, the overall mean metacognitive level of Class A increased from 96.55 to 108.51, while the mathematical metacognitive level increased from “average” to “above average.” The percentage level of each first-level dimension increased, with the MME dimension increasing the most and the MMM dimension increasing the least.Paired-samples t-tests were conducted on the pre- and post-intervention scores of each dimension of mathematical metacognition in Class A. Significant differences were found in the scores of each dimension (p<0.05), and the Effect Size (ES) was further calculated. The differences in overall mathematical metacognition and each first-level dimension before and after the intervention were found to have a large effect (ES>0.8), indicating that the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System’s improvement strategy was effective in improving the overall level of mathematical metacognition and each dimension of the tested classes.

The average of the three pre-test mathematics scores of each student in the tested class was used as the students’ mathematics learning level. According to Zhang X and Yu’s [9] classification standard of academic levels, the students were divided into groups with high, ordinary, and low scores. The data analysis revealed that after the intervention was implemented according to the intelligence improvement strategy, all three groups of students had a significant increase in mathematical metacognition (p<0.05), with large effect sizes (ES>0.8). By comparing the values of the effect sizes, the groups with high and ordinary scores were found to have a higher degree of mathematical metacognitive improvement than the group with low scores.

This intervention revealed that the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System was effective in promoting the improvement of students’ mathematical metacognition. The results further verified the findings of existing studies [10] that metacognitive guidance is effective in improving students’ level of metacognition. Furthermore, it was found that the intelligence improvement strategies given by the system significantly improved students of different grade levels, and the improvement degree of the groups with high and ordinary scores was higher than that of the group with low scores. This is consistent with the findings of existing studies [11] but not with teachers’ judgments from teaching experience.The interviews revealed that mathematics teachers usually perceived that the metacognitive level of the group with higher scores was inherently higher and that there was relatively little room for improvement. However, the sample of students selected for the study generally had low learning efficiency and a heavy learning burden, and the mathematical metacognition of students at different learning levels was not optimistic.

Under these circumstances, students in the group with higher scores did not have high learning efficiency, even though they had achieved relatively satisfactory academic performance. One piece of evidence indicates that the pre-test found that the mean value of mathematical metacognition among students in the group with high scores was 117.17, which is above average in Tianjin. This reveals that the mathematical metacognitive level of the group with high scores is not ideal, with few excellent scores, therefore leaving some room for improvement. In contrast, students in the group with high scores tended to possess strong learning abilities and execution. When they encounter their own metacognitive problems, they will better implement the program, improving their level of mathematical metacognition. This is consistent with this paper’s intervention results and further verifies that the improvement in mathematical metacognitive level can improve learning efficiency and thus achieve higher academic achievement [7]. For students in the group with lower scores, their mathematical knowledge was relatively weak. They lacked ideas for solving mathematical problems and often lacked good study habits. Therefore, although the overall improvement effect was significant, it was not as good as the improvement effect in the groups with high and ordinary scores.

Overall, the Mathematics Learning Quality Intelligent Assessment and Strategy Implementation System’s intelligent diagnosis and implementation of its mathematical metacognitive improvement strategies were effective in improving students’ mathematical metacognitive levels. The improvement of students’ mathematical metacognition was significant across all groups of students with different levels of mathematical learning performance. Specifically, students in the groups with high and ordinary scores exhibited better improvement than those in the group with low scores.

This research was funded by the Tianjin Research Innovation Project for Postgraduate Students, grant number 2021YJSB323. Cuiying Chang collected and analyzed the data. Guangming Wang and Yiming Zhen wrote the manuscript. Yiming Zhen provided the funding.

1. Flavell J (1979) Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. American Psychologist 34(10): 906-911.
2. Luo Y (2019) Analysis of the relationship between critical thinking and metacognition. Theory and Practice of Education 39(23): 3-5.
3. Vats D, Kaushik P (2016) Meta-cognitive awareness and personality as predictors of creativity among young adults. Journal of Contemporary Psychological Research 2: 30-40.
4. Hoffman B, Spatariu A (2008) The influence of self-efficacy and metacognitive prompting on math problem-solving efficiency. Contemporary Educational Psychology 33(4): 875-893.
5. Gomes CMA, Golino HF, Menezes IG (2014) Predicting school achievement rather than intelligence: Does metacognition matter? Psychology 5(9): 1095-1110.
6. Zhao N, Teng X, Li W, Li Y, Wang S, et al. (2019) A path model for metacognition and its relation to problem-solving strategies and achievement for different tasks. ZDM-Mathematics Education 51(4): 641-653.
7. Wang G, Zhen Y, Chen X,Kang Y, Cui B (2022) Mathematical metacognitive characteristics of Chinese middle school students in efficient mathematics learning. ZDM-Mathematics Education 54(3): 543-554.
8. Wang G, Kang Y, Chen X (2022) Research on intelligent assessment of mathematics learning quality of primary and secondary school students: taking mathematical metacognition as an example. Eliva Press, Moldova, Europe, p. 173.
9. Zhang X, Yu P (2011) A Study on the differences of mathematical problem schemas of students at different academic levels. Journal of Mathematics Education 20(1): 45-48.
10. Mutambuki JM, Mwavita M, Muteti CZ, Jacob BI, Mohanty S (2020) Metacognition and active learning combination reveals better performance on cognitively demanding general chemistry concepts than active learning alone. Journal of Chemical Education 97(7): 1832-1840.
11. Wang J (2017) Effects of metacognition training on improving metacognition level and application problem scores of senior primary school students. Doctoral Thesis, China.