- Submissions

Full Text
Psychology and Psychotherapy: Research Study
Understanding Differential Item Functioning and Item bias In Psychological Instruments
Insu Paek*
Department of Psychology, Florida State University, USA
*Corresponding author: Insu Paek, Associate professor Measurement & Statistics Program Educational Psychology & Learning Systems, Florida State University, Tallahassee, USA
Submission: March 09, 2018;Published: May 27, 2018

ISSN 2639-0612Volume1 Issue3
Introduction
For a psychological test or instrument to function properly as intended, items in the test should measure respondents’ performance fairly across different groups of respondents such as male and female. In psychometric literature, the concept of differential item functioning (DIF) has been introduced to address the differential group performance on an item when the groups are equated at the same level of ability or latent trait status. This article introduces the concept of DIF while making a clear distinction of DIF from item bias and simple group performance difference since the civil rights error of the 1960’s in the United States, inequity has become a critical social issue. The area of educational and psychological testing is no exception. The use of testing as a sorting mechanism [1] has brought equity concerns to many people, specifically the testing enterprise.
Academic research on group differences and public awareness of them has resulted in the examination of whether tests in educational and psychological testing are disadvantaging minority groups. A well-known incident with regard to bias issue and group differences is “Golden Rule” settlement in 1984. The Golden Rule insurance company in 1976 filed a lawsuit against Illinois Department of Insurance and Educational Testing Service, charging racial bias in Illinois insurance licensing exams. The lawsuit led to an out-of-court settlement, ending the 8-year-old suit. The gist of the settlement was elimination of any items showing different item proportion correct (i.e., proportion of yes/correct answers in an item which is called “item p-value” or “marginal item proportioncorrect) across the compared groups. (see for detail, e.g., [2].
Even before the Golden Rule settlement, there was a claim in the academic community that some tests (e.g., IQ test) are biased against minority groups. Researchers claim the bias usually investigated item p-value and considered an item to be biased if it showed a big difference in the item p-value between the compared groups (e.g., white majority groups vs. black minority group). This approach is consistent with the solution suggested by the Golden Rule settlement. However, this approach of using the marginal item proportion-correct is flawed because it does not distinguish the true group difference and the true bias. This drawback of the Golden Rule settlement procedure has been pointed out by many academic researchers. For example, Gregory R. Anrig, the president of Educational Testing Served announced that the Golden Rule settlement was “an error of judgment” (see also for the side effect of executing the Golden Rule procedure, e.g., [3,4]. One could ask “Is it right to make group differences negligible by manipulating the test items (by excluding and revising items) if there is actually a real group difference possibly created by past or present social inequity?”
Technically the major drawback of this marginal proportion correct approach is the confounding of group difference and real bias. The marginal probability of item correct is affected by the population distribution – related to group mean difference – and by the item response function – related to item bias. That is, the marginal probability (observed proportion correct or incorrect) is represented as
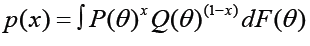
where P(x) is a marginal probability of either x= Yes/correct or x=No/incorrect,θ is a person latent trait or ability), P(θ) is the item response function, Q(θ)=1−P(θ) and F(θ) is the distribution of θ. In the above− presentation, one can see that person latent trait/ability and item characteristics are confounded in the observed proportion of x. (Note that a similar equation can be expressed for the Likert style item response items or graded response item responses, showing that the observed marginal score is based on both item response function and the latent trait distribution.) If we see a large difference in the proportion correct between the two groups, we cannot draw the conclusion that the item is really biased. The large difference could be due to either a real group difference between the two groups or to a bias factor disadvantaging one group; or it could be both factors, which is probably the case in many real world applications [5].
In subsequent years, the definition of bias and the methodology of its detection have been refined. The word “bias” is now replaced by a term, “Differential Item Functioning” (DIF), at least in academia. Because of the social connotation of the word, “bias”, Holland and Thayer (1988) suggested the alternative term DIF in place of “bias”. The complexity of the usage of these terms has been a source of confusion of the communication between the technical measurement community and the public [6]. DIF is a neutral term, indicating the magnitude of advantage or disadvantage presented by an item to a particular group, which is usually estimated through statistical analysis. In recent years, identifying DIF items and classifying some (or all) of those DIF items as biased items are considered separate. The former is a statistical concept while the latter is more than statistical including the interpretation of the identified DIF in the context of social justice.
A formal definition of no DIF [3,6,8] can be given as follows.
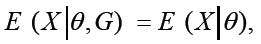
where E is the expectation operator, X is a categorical ordinal item response (e.g., X = 1 (strongly disagree), 2 (disagree), 3 (agree), or 4 (strongly agree) in the 4-option Likerty style item test), G is a group indicator (e.g., 1 = Female and 0 = Male; 1 = African American and 0 = White), and θ is person latent trait/ ability. Sometimes, no DIF is expressed using an observed variable Z instead of θ , which is a proxy for θ . The above definition of no DIF states, in words, that there is no DIF if the expected item score for one group and the expected item score for the other group are the same when the latent trait/ability scores are equated. Again, DIF is about a conditional comparison between the two compared groups on the same trait/ability level, not a marginal comparison. Those who would like to know more about the methods of DIF detection are referred to [7,8].
From the test validity point of view, DIF and its detection are of importance and the existence of DIF call into question the fairness of testing. Although a test constructed without DIF cannot undo the past inequalities, it can reveal the inequalities which may have been created by past and existing inequity, thereby giving people a chance to think of the source of such a difference.
References
- Glaser R (1981) The future of testing. American Psychologist 36(9): 923- 936.
- Faggen J (1987) Golden Rule Revisited: Introduction. Educational Measurement: Issues and Practice 6(2): 5-8.
- Chang H, Mazzeo J, Roussos L (1996) Detecting DIF for polytomously scored items: an adaption of the SIBTEST procedure. Journal of Educational Measurement 33(3): 333-353.
- Linn RL, Drasgow F (1987) Implications of the Golden Rule settlement for test construction. Educational Measurement: Issues and Practice 6(2): 13-17.
- Cole NS (1983) History and development of DIF. In: PW Holland & H. Wainer (Eds.), Differential Item Functioning, Lawrence Erlbaum Associate, Hillsdale, NJ, USA, p. 25-29.
- Lord FM (1977) A study of item bias, using item characteristic curve theory. In: YH Portinga (Ed.), Basic problems in cross-cultural psychology, Swets and Zeitlinger, Amsterdam, Netherlands, p. 19-29.
- Shealy R, Stout W (1993) A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 58(2): 159-194.
- Thissen D, Steinberg L, Wainer H (1993) Detection of differential item functioning using the parameters of item response models. In: PW Holland & H Wainer (Eds.), Differential Item Functioning, Lawrence Erlbaum Associates, Hillsdale, NJ, USA, pp. 67-113.
© 2018 Insu Paek. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






