A Survey on Trigonometric Measures of Fuzzy Information and Discrimination

Introduction

When proposing fuzzy set, [2] concerns were explicitly centred on their potential contribution in the domain of pattern classification, processing and communication of information, abstraction, summarization, etc. Although the claims that fuzzy sets were relevant in these areas appeared unsustainable in the early sixties, however, the future development of information science and engineering proved that these intuitions were right.

The specificity of fuzzy sets is to capture the idea of partial membership. The characteristic function of a fuzzy set is often called membership function and the role of that has well been explained by Singpurwalla & Booker [3] in probability measures of fuzzy sets. A generalized theory of uncertainty has been well explained by Zadeh [4] where he remarked that uncertainty was an attribute of information. Before that the path breaking work of Shannon [5] had led to a universal acceptance of the theory that information was statistical in nature. However, a perception-based theory of probabilistic reasoning with imprecise probabilities was explained by Zadeh [4]. Taking into consideration the concept of fuzzy set, De Luca & Termini [6] suggested that corresponding to Shannon’s [5] probabilistic entropy, the measure of fuzzy information could be defined as follows:

Where 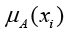are the membership values?

Bhandari & Pal [7] parametrically generalized (1.1) as given below:

On the same lines many researchers have studied various generalized fuzzy information measures. Hooda [8] and Hooda & Bajaj [9] and many more have studied various generalized additive and non-additive fuzzy information measures. Hooda & Jain [10] characterized sub additive trigonometric measure of fuzzy information corresponding to probabilistic entropy studied by Sharma & Taneja [2]. It may be noted that trigonometric measures has its own importance in application point of view, particularly in geometry.

Sine and Cosine Trigonometric Fuzzy Information Measures

Most of fuzzy information measures have been defined analogous to probabilistic entropies. Hooda & Mishra [1] introduced two trigonometric fuzzy information measures which have no analogous probabilistic entropies as given below:

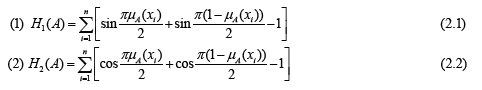
First of all we check the validity of the proposed measures (2.1) and (2.2).

Theorem 1

The fuzzy information measure given by (2.1) is valid measure.

Proof: To prove that the given measure is a valid measure, we shall show that (2.1) satisfies the four properties (P1) to (P4).

(P1). H₁(A ) = 0 if and only if A is a crisp set.

Evidently,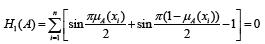if and only if either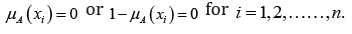

It implies if and only if A is a crisp set.

(P2). H₂(A ) is maximum if and only if A is the fuzziest set 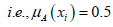for all i =1, 2,……, n.

Differentiating H₁(A ) with respect to μ_A(x_i) , we have

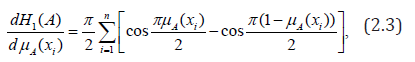
which vanishes at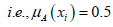

Again differentiating (2.3) with respect to , we get

which is less than zero (<0) at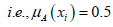

Hence H₁(A ) is maximum at μ_A(x_i) for i =1, 2,……, n.

Further from (2.3) we see that H₁(A ) is an increasing function μ_A(x_i) in t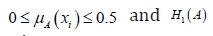he region is a decreasing function of μ_A(x_i) in the region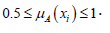

(P3). Let A* be sharpened version of A, which means that

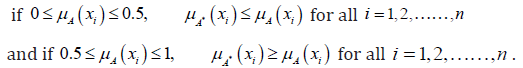
Since H₁(A ) is an increasing function of μ_A(x_i) in the region 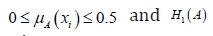is a decreasing function of μ_A(x_i) in the region 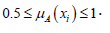therefore

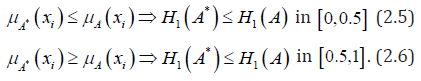
Hence (2.5) and (2.6) together give

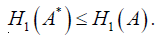
(P4). From the definition It is evident that

where is complement of A obtained by replacing μ_A(x_i) by 1-μ_A(x_i)

Hence H₁(A) satisfies all the essential four properties of fuzzy information measures. Thus, it is a valid measure of fuzzy information. On the same line it can be proved that H₂(A) is a valid fuzzy information measure. By considering a concave function sinπ x ,∀ x∈[0, 1 ] , Hooda & Mishra [1] defined the following fuzzy information measure and proved its validity:

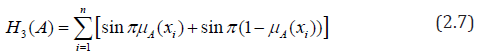
Theorem 2

The fuzzy information measure given by (2.7) is valid measure.

Proof: To prove that the given measure is a valid measure, we shall show that (2.7) satisfies the four properties (P1) to (P4).

(P1). H₃(A) = 0 if and only if A is a crisp set.

Evidently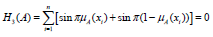 if and only if either μ_A(x_i) by 1-μ_A(x_i) for i =1, 2,……, n.

It implies H₃(A) = 0 if and only if A is a crisp set

(P2). H₃(A) is maximum if and only if A is the fuzziest set

H₃(A ) is maximum if and only if A is the fuzziest set 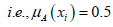for all i =1, 2,……, n

Differentiating H₃(A ) with respect to μ_A(x_i) , we have

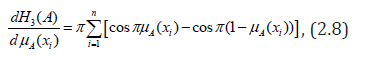
which vanishes at μ_A(x_i)=0.5

Again differentiating (2.8) with respect to μ_A(x_i),we get

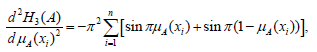
which is less than zero (< 0) at μ_A(x_i)=0.5

Hence H₃(A ) is maximum at μ_A(x_i) for i =1, 2,……, n.

H₃(A) is an increasing function of μ_A(x_i) in the region 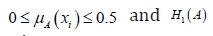and H₃(A) is a decreasing function of μ_A(x_i) in the region .

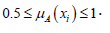(P3). Let A* be sharpened version of A, which means that

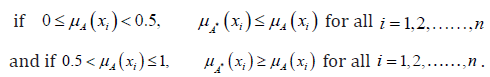
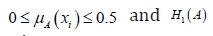Since H₃(A) is an increasing function of μ_A(x_i) in the region and H₃(A) is a decreasing function of μ_A(x_i) in the region 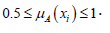.Therefore,

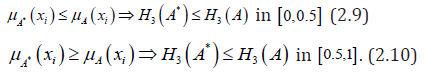
Hence (2.9) and (2.10) together give

where is complement of A obtained by replacing μ_A(x_i) by 1-μ_A(x_i)

Hence H₃(A) satisfies all the essential four properties of fuzzy information measures. Thus it is a valid measure of fuzzy information.

Further they defined generalized sine trigonometric fuzzy information measure as given below:

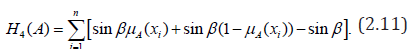
It may be noted that (2.11) reduces to (2.7) when β =π and reduces to (2.1) when β =π/2

Another generalized sine trigonometric measure of fuzzy information is

In particular when α = 0, (2.12) reduces to (2.11) and reduces to (2.7) when α = 0 and β =π .

A generalized cosine trigonometric measure of fuzzy information is defined as

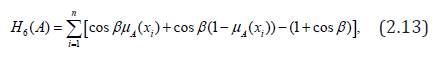
which is a new generalized cosine trigonometric measure of fuzzy information and it reduces to the following fuzzy information measure when β =π/2

It can be easily verified that these fuzzy information measure satisfy the essential properties of validity.

A New Cosine Fuzzy Information Measure

Let X={x₁,x₂,....,c_n} be a set of universe and A be a fuzzy set in X having membership function μ_A(x_i) defined on X. Then cosine fuzzy information measure for fuzzy set A was defined as

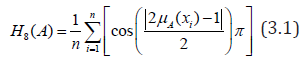
Theorem 3

H (A) is a valid fuzzy information measure?

Proof: For validity of the measure we shall prove that the following four essential properties (P1) to (P4) are satisfied:

(P1). H₈(A) = 0 if and only if A is a crisp set.

Evidently H₈(A) = 0 if and only if either μ_A(x_i)=0 or 1-μ_A(x_i) for i =1, 2,……, n.

(P2). H₈(A) is maximum if μ_A(x_i)=0.5 for all i =1, 2,……, n.

Differentiating H₈(A) with respect to μ_A(x_i) , we have

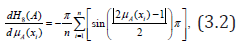
which reduces to zero when μ_A(x_i)=0.5 for all i =1, 2,……, n

Differentiating again, we get

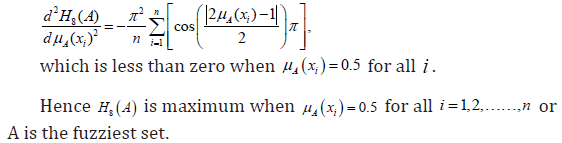
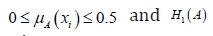Further it may be noted that H₈(A) is an increasing function of μ_A(x_i) in the region is a decreasing function of μ_A(x_i) in the region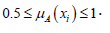

(P3). Let A* be sharpened version of A, then

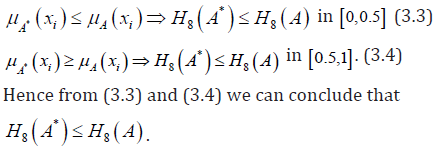
(P4). It is evident that if μ_A(x_i) replacing by 1-μ_A(x_i) for all i =1, 2,……, n , then

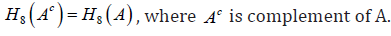
Theorem 4

Let X={x₁,x₂,....,c_n} be the universe of discourse. Let A and B be two fuzzy set in a fixed universe of discourse X. Let A(x_i)=μ_A(x_i) and B(x_i)=μ_B(x_i) satisfying either A ⊆ B or B ⊆ A , then the following holds:

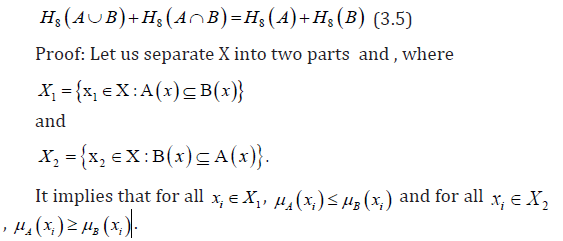
From (3.1), we have

Tangent Inverse Trigonometric Fuzzy Information Measure

Prakash and Gandhi [11] proposed the following tangent fuzzy information measure:

They proved that (4.1) was a valid fuzzy measure and applied to the geometry to estimate the perimeter and area of polygon. Next, Hooda and Mishra [1] defined tangent inverse trigonometric fuzzy information measure and prove its validity.

Definition 4.1

Let X={x₁,x₂,....,c_n} be a set of universe and A be a fuzzy set in X having membership function μ_A(x_i) defined on X. Then tangent inverse trigonometric fuzzy information measure for fuzzy set A is defined as

Theorem 5

The measure in (4.2) is a valid fuzzy information measure.

Proof: To prove that the measure (4.2) is a valid measure, we shall show that it is satisfying the four properties (P1) to (P4).

(P1). H_α(A)=0 if and only if A is a crisp set.

If μ_A(x_i)=0 or 1-μ_A(x_i)=0 , H_α(A)=0 .

Hence H_α(A)=0 if A is crisp set, . . μ_A(x_i)=0 or 1-μ_A(x_i)=0 for i =1, 2,……, n.

Conversely, H_α(A)=0 , then

The equality holds if either μ_A(x_i)=0 or 1-μ_A(x_i)=0 i.e. A is a crisp set.

Thus H_α(A)=0 if and only if A is a crisp set, . . μ_A(x_i)=0 or 1-μ_A(x_i)=0 for i =1, 2,……, n.

(P2). H_α(A) is maximum if and only if A is the fuzziest set, for i =1, 2,……, n.

Differentiating (4.2) with respect to μ_A(x_i) , we have

Again differentiating (4.3) with respect to μ_A(x_i) , we have

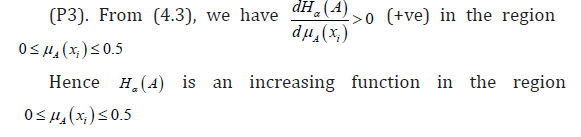
Similarly, from (4.3) in the region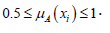

Hence H_α(A) is decreasing function in the region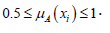

Let A* be the sharpend version of A, then

Since H_α(A) satisfies all the properties of fuzzy information measure, therefore, it is a valid measure of fuzzy information.

Particular Case: When α→1, (4.2) reduces to De Luca and Termini [6] fuzzy information measure.

A Generalized Measure of Fuzzy Discrimination

Analogous to Kullback and Liebler 1951, Bhandari and Pal [12] suggested the simplest measure of fuzzy discrimination as follows:

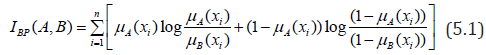
Analogous to (4.2), Hooda and Mishra [1] defined a new inverse tangent fuzzy discrimination measure as follows:

Definition 5.1

The fuzzy discrimination measure is said to be valid if it satisfies

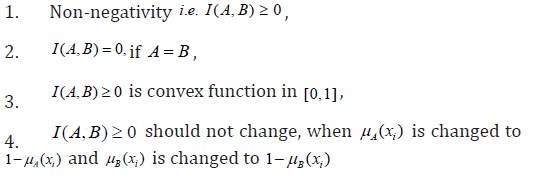
Theorem 6

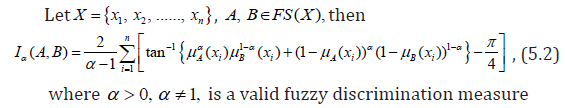
Proof: It can be easily verified that I (A, B) α satisfy all four properties from (i) to (iv). Thus, it is a valid generalized measure of fuzzy discrimination.

Application of Fuzzy Discrimination in Strategic Decision Making

In current scenario, the applications of the fuzzy discrimination measure in various fields have been studied, namely, in bioinformatics by Poletti et al. [13] and Fan et al. [14]. Bhatia and Singh [15] discussed in image thresholding, Ghosh et al. [16] applied it in automated leukocyte recognition. Here, the application of the above fuzzy discrimination measure in strategic decision making is proposed and studied.

Decision making problem is the process of finding the optimal solution from all the existing feasible alternatives. It is assumed that a firm Y desires to apply m strategies {S₁,S₂,.....,S_n} to meet its goal. Let each strategy has different degree of effectiveness. If it has different input associated with it, then let it be{l₁,l₂,.....,l_n}. The fuzzy set Y denotes the effectiveness of a particular strategy with uniform input. Then,

It is assumed that I_t(1≤ t ≤ n) determines the minimum value 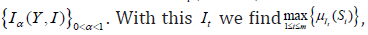let it correspond to S_p(1≤ p ≤ m) . Hence, if the strategy p S is implemented with input budget of t I the firm will meet its goal in the most input effective manner

Numerical Illustration

Let m = n = 5 in the above model. Table 1 shows the efficiency of different strategies at uniform inputs. Table 2 illustrates the efficiency of different strategies at particular inputs and Table 3 the numerical values of discrimination measure

Table 1:Efficiency of different strategies at uniform inputs.

Table 2:Efficiency of different strategies at particular inputs.

Table 3:Numerical values of discrimination measure { }1 I_α (Y, I )

The calculated numerical data of the proposed fuzzy discrimination measure indicates that input is more suitable. The assessment of the results existing in Table 2 and Table 3 points out that strategy is most effectual. Thus, a firm will achieve its goal most efficiently if the strategy is applied with an input.

References

1. Hooda DS, Mishra AR (2015) On trigonometric fuzzy information measures. ARPN journal of Science and Technology 5(3): 145-152.
2. Sharma BD, Taneja IJ (1977) Three generalized additive measures of entropy. Elec Inform Kybern 13: 419-433.
3. Singpurwalla ND, Booker JM (2004) Membership function and probability measure of fuzzy sets. J Amer Stat Assoc 99(467): 867-889.
4. Zadeh LA (1965) Fuzzy sets. Information and Control 8(3): 338-353.
5. Shannon E (1948) A mathematical theory of communication. Bell Syst Tech J 27: 379-423 & 623-659.
6. DeLuca A, Termini S (1972) A definition of non-probabilistic entropy in setting of fuzzy set theory. Inform Contr 20(4): 301-312.
7. Bhandari D, Pal NR (1993) Some new information measures of fuzzy sets. Information Sciences 67(3): 204-228.
8. Hooda DS (2004) On generalized measures of fuzzy entropy. Mathematica Slovaka 54(3): 315-325.
9. Hooda DS, Divya Jain (2010) Sub additive measures of fuzzy information. Journal of Reliability and Statistical Studies 2(2): 39-52.
10. Hooda DS, Bajaj RK (2008) On generalized R-norm measures of fuzzy information. Journal of Applied Mathematics Statistics and Information 4: 199-212.
11. Prakash O, Gandhi CP (2010) Applications of trigonometric measures of fuzzy entropy to geometry. World Academy 0f Science Engineering and Technology 37: 468-471.
12. Bhandari D, Pal NR, Majumder DD (1992) Fuzzy divergence, probability measure of fuzzy events and image thresholding. Pattern Recognition Letters 13(12): 857-867.
13. Poletti E, Zappeli F, Ruggeri A, Grisan E (2012) A review of Thresholding strategies applied to human chromosome segmentation. Computer Methods and Programs in Biomedicine 108(2): 679-688.
14. Fan S, Yang S, He P, Nie H (2011) Infrared electric image thresholding using two dimensional fuzzy entropy. Energy Procedia 12: 411-419.
15. Bhatia PK, Singh S (2013) A new measure of fuzzy directed divergence and its application in image segmentation. International Journal of intelligent system and applications 4: 81-89.
16. Ghosh M, Das D, Chakraborty C, Roy AK (2010) Automated leukocyte recognition using fuzzy divergence. Micron 41(7): 840-846.