- Submissions

Full Text
Novel Research in Sciences
Speed : A Concept or A Phenomenon?
Patrice F Dassonville*
Freelance Researcher, France
*Corresponding author: Patrice F Dassonville, Freelance Researcher, France
Submission: November 8, 2021;Published: December 02, 2021
.jpg)
Volume10 Issue1December, 2021
Abstract
Whatever the way to define it, the speed has no physical properties. Several applications confirm that the speed is not a phenomenon. Instead, it’s a concept.
Keywords: Experiment; Measure; Property
Introduction
The speed of a system can be defined in two ways: either a passive definition or an active
definition. In addition, it appears through three experiments that the speed is not the cause of
the observed phenomena:
i. The cause of accumulation of cars on bends.
ii. The cause of car traffic jam.
iii. The covariance of speed in special relativity.
A passive definition
We have a passive definition when the speed of a system results from the ratio between the space travelled by the system and the duration of the travel:

The wording of the definition is:

Considering that «distance», «space», «time» and «duration» have already been defined elsewhere [1], we are allowed to use these words in order to simplify the wordings. The definition of speed becomes :

Given that space and time are concepts [2], the mathematical ratio between space and time is a mathematical concept instead of a phenomenon.
An active definition
In life of Sylla, the Greek biographer Plutarch (c.46-c.125) makes a clever observation : «[Sylla] shortened the space between his army and the barbarians, thanks to the velocity of his troops» [3]. Velocity is from the latin velocitas [4], that we find in the Latin scholar Cicero (106-43), the Roman strategist cesar (101-144), the latin writer pliny (61-c.114), the latin historian tacitus (c.55-c.120): it’s the capability of moving fast. We have an active definition when the previous equation is written :
«v» looks like being the cause of the move; indeed, if the value
of «v» is zero, that of «l» is zero, regardless the value of «t». Hence
the definition : The Speed «v» is the ability of a system to change
its position.
When analyzing the equation «l=v.t», we must beware of the
field model effects :
i. «t» is what the clock indicates: it has no action on the
movement.
ii. As a mathematical parameter, «v» gives the system the ability
to move.
iii. There are no speed experiments: we don’t observe the speed,
instead, we observe the system (example with the cars below);
we don’t measure speed either: measures are done on the
system (the cars below); they concern what the system and the
clock are doing. It confirms that the speed is not a phenomenon.
Speed in bends
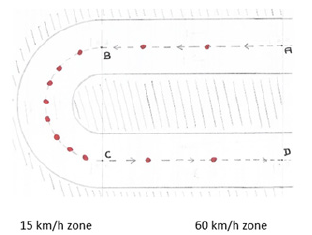
The turns oblige the driver to slow down; and the reduction in speed makes cars spend more time in the bends than in the straights. Let’s take an example with a car driven at 60km/h on parts «AB» and «CD» of the road, and at 15km/h in the turn «BC» : the car is going to stay 4 times longer in this area than in the straights (Figure 1). It explains why, in the mountains, we meet cars especially on bends. The physical cause of the slowdown is the turn, not the speed.
Figure 1: Accumulation of cars on bends.
Speed and car traffic jam
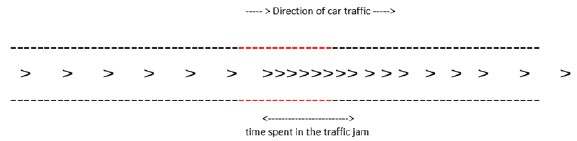
a) The slowdown zone & traffic jam: Cars > enter the slowdown area faster than they leave it; the return to average speed is slow (Figure 2). Therefore, the slowdown zone leads to the development to a traffic jam (Figure 3).
Figure 2: Start of a traffic jam.
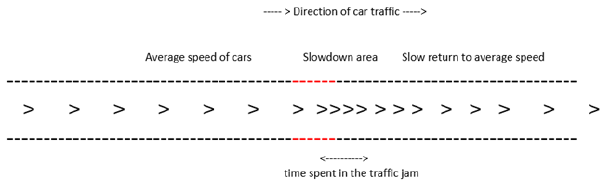
Figure 3: Development of the traffic jam.
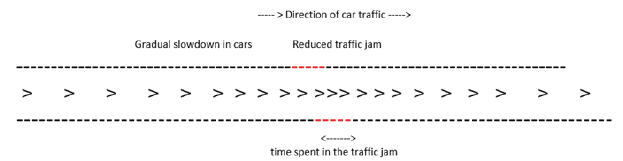
b) Role of a deceleration zone: Implementing a gradual deceleration zone leads to reduce the traffic jam because cars enter the slowdown zone less quickly. Then, time spent in the slowdown zone does not increase (Figure 4). Traffic jams are not caused by the speed, but by cars driven at inappropriate speeds.
Figure 4: Effect of a slowdown zone.
The Covariance of Speed in Special Relativity
It concerns systems travelling at speed closed to that of light, called relativistic speed, like particles in an accelerator. The word «covariance» means that what we observe from the laboratory differs from what happens inside the relativistic system. For example, durations look longer, lengths look shorter, etc. All parameters are covariant and the classical laws of mechanics must be replaced by laws of special relativity (Einstein 1905) in order to restore the exact data. Example with two systems moving in opposite directions at speeds «V1» and «V2» in relation to a fixed benchmark (Figure 5); how fast are they moving away from each other? In classical machanics speeds can be added and the answer is :
Figure 5: Movements in opposite directions.

If «V1» or «V2» is a relativistic speed, like particles inside an accelerator, the addition is no more allowed :
According to Special Relativity, the speeds are not added, but composed by using the transformation of Lorentz [5] :
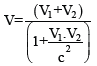
in which «c» is the speed of light.
Reminder
These experiments above are done on physical systems (cars, particles, etc.), not on their respective speed.
Physical Properties of the Speed
The speed is not observable and not measurable as such.
No experiments can be done on the speed: it’s the symptom of
the absence of physical properties. Therefore the speed is not a
phenomenon; instead, it’s a mathematical concept. In contrast, as
for time and space [1], it has mathematical properties that depend
on the field of study, and among which we can mention:
i. In classical physics: continuous, reversible, invariant.
ii. In quantum physics: stochastic, discontinuous, irreversible,
invariant.
iii. In relativistic physics: continuous, reversible, covariant.
iv. In relativistic quantum physics: stochastic, discontinuous,
irreversible, covariant.
Conclusion
Two different ways of defining speed showed that it’s not a phenomenon. This result has been confirmed through several experiments in classical mechanics and through a relativistic situation. We must beware of field model effects and technical effects of field: it’s important to emphasize that these experiments were done on systems, instead of speeds as such. At large, the speed has no physical properties: it’s a polymorphic concept.
References
- Dassonville P (2012) The non-existence of time. Perseus.
- Dassonville P (2017) The invention of time & space: Origins, definitions, nature, properties. (1st edn), Springer publishers, USA, pp. 1-176.
- Plutarch (2001) Parallel Lives. pp. 1-864.
- Félix G, Pierre F (2012) Le Grand Gaffiot: Latin French Dictionary. (3rd edn), Hachette publishers, France, pp. 1-1766.
- Mavridès S (1988) Relativity. (4th edn), Presses Universitaires de France, France.
© 2021 Patrice F Dassonville. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)














.bmp)
.jpg)
.png)
.jpg)










.jpg)






.png)

.png)



.png)






