Particle Phase Recognition Based on KNN Algorithm for Spaceborne Dual Frequency Radar

It is significant to acquaint with microphysical characteristics for studying structural features and evolutionary rules of different types of precipitation. As one of the main microphysical characteristics, particle phase plays an important role in fields of raindrop spectrum retrieval, monitoring and early warning for disastrous weather, numerical weather prediction, and weather modification [1]. In 2014, GPM (Global Precipitation Measurement) satellite was launched successfully, which carried DPR (Dual-frequency Precipitation Radar) consisted of KuPR (13.6GHz) and KaPR (35.5GHz). DPR has a wide range of observations and improve the detection for weak rainfall and snowfall. Although DPR provides rich observational data about precipitation, there are few studies on phase recognition with DPR data. Wu et al. [2] differentiated the rainfall and the snowfall based on the phase products and the air temperature profiles of DPR data. According to the results of the 4 snowfall examples, it was difficult to differentiate mixed phase and liquid phase from the view of temperature when the temperature at solid phase was below -0.5 ℃, but overall phase products of DPR were consistent with practical weather processes. Le et al. [3] proposed an algorithm for recognizing ground snowfall, which mainly calculated the Snowfall Index (SI) based on the vertical profile of radar echo, instead of near-ground echo only. As a result, the omission due to the intensity of near-ground echo lower than the minimum detectable echo of DPR was avoided during snowfall. This method now has been used in products of DPR V5 and the versions above. Based on Le’s SI algorithm, Li et al. [4] improved the method of quality control for reflectivity factor and calculated the slope of DFRm vertical profile. As a result, the recognition effect of rainfall and snowfall in winter was greatly improved. Liao et al. [5] hypothesized that the rainfall followed Marshall-Palmer distribution and the snowfall followed Gunn-Marshall distribution, simulated the relationship between reflectivity factors at Ku band Z_eK_u and DFR of rainfall and snowfall with different phases under different precipitation rates (R), and superposed observational data of airborne APR to Z_eK_u-DFR plane. The results indicated that the recognition effect on rainfall and snowfall was the best. For mixed phase and rainfall, although certain overlap occurred in some regions, the overall recognition was acceptable. From the view of scattering characteristics difference of particles with different phases (solid, liquid and mixed), this paper simulates reflectivity factor of particles at Ku and Ka band by the T-matrix method, analyzes the feasibility of recognizing precipitation phase at the two bands of DPR, then trains the KNN algorithm on Z_eK_u-DFR plane based on the simulation results and uses the trained KNN algorithm for recognizing precipitation phase.

This paper simulates the back scattering section and the reflectivity factor by the T-matrix method. Waterman et al. [6] created the T-matrix method which provided a strict solution to the scattering problem of homogeneous non-spherical conductor and subsequently extended to the scattering problem of non-spherical dielectric. Mishchenko et al. [7] further improved the T-matrix method and realized more mature theoretical and computational procedure and a wider scope of application. T-matrix is not related to specific incident field, so that the scattered field can be calculated after getting T-matrix, and then the scattering section can be calculated in any direction [8]. KNN (K-Nearest Neighbor) algorithm is a basic classification and regression method proposed by Cover & Hart [9] in 1967. As one of the simplest methods in data classification technology, it can be understood and applied easily. K-nearest neighbor means K number of nearest neighbors, that is to say, each sample can be indicated with K number of its nearest neighbors (the shortest distance is generally used to indicate “nearest”). If most of the neighbors come from a certain category, the sample also can be included in this category with the process as below:

1. Calculate the distance between tested data and each trained data.?
2. Rank upon distance in ascending order.?
3. Select K number of points with minimum distance.?
4. Determine the frequency of the category to which the previous K number of points belong.?
5. Return the category with the highest frequency among the previous K number of points as prediction category for tested data.

Theoretical simulation and phase recognition with KNN algorithm

In order to simulate the equivalent reflectivity factor of precipitation particles at Ku and Ka band by the T-matrix method, it is necessary to hypothesize the particle size distribution model. This paper uses the Gamma distribution model in three-parameter form as below:

(1)

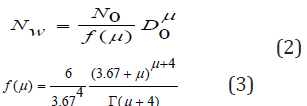
where, D₀ is the mid-value diameter (mm), N_w is the total number of particles per unit volume (m^-3), is the spectral diameter, and  is Gamma function. Based on Gamma distribution, back scattering section is calculated by the T-matrix method and then integrated to get the equivalent reflectivity factor Ze as below:

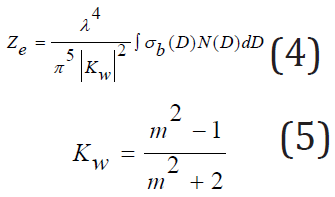
where, λ is the wavelength of radar, m is the complex refractive index of particle,  is the back scattering section of particle and N(D) is the spectral distribution of particles [10]. When the complex refractive index of particle is calculated, if the particle is oblate ellipsoid, Debye model is used for mixed and solid particles, with temperature setting at 0 ℃. The mixed particle is mixed from solid and liquid particle, with volume ratio 0.2, 0.5 and 0.8 respectively. The solid particle is ice-air mixture, with density 0.2g/cm³,0.5g/cm³ and 0.8g/cm³ respectively. Liebe model is used for liquid particle [11]. In order to describe the difference between equivalent reflectivity factors at Ka and Ku band, DFR is defined as below:

DFR= 101 lg(Z_eK_u ) 101g(Z_eK_a ) (6)

where, Z_eK_u is the equivalent reflectivity factor at Ku band and Z_eK_a is the equivalent refractivity factor at Ka band. This paper simulates DFR and Z_eK_u of particles with different phases using Gamma distribution. Different types of precipitation indicate different particle spectrum [12], so that for stratiform precipitation, D0 is set within 1mm and 1.5mm and the step size is set to 0.02mm; N_w is set within 104 and 105 with the step size 3600, μ=3; the particle phase is solid, liquid and mixed. For convective precipitation, D₀ is set within 1.5mm and 2.5mm with the step size 0.04mm; N_w is set within 10³ and 10⁴ with the step size 3600, μ=3; the particle phase is solid and liquid. The liquid particle is not sensitive to the temperature, so that the temperature is set to 288K in simulation. Figure 1 shows the relationship between DFR and Z_eK_u of particles in different phases for different types of precipitation.

Figure 1: Simulation results for different phases of particles. a) stratiform precipitation and b) convective precipitation.

According to Figure 1a, for stratiform precipitation, Z_eK_u and DFR of particles with three phases have a positive correlation. When Z_eK_u is certain, DFR of solid, mixed and liquid particles decreases successively. For solid particles, DFR is larger than 0dBZ and Z_eK_u is within 10dBZ and 40dBZ. For mixed particles, DFR is also larger than 0dBZ and its maximum is larger than liquid and solid particles, and Z_eK_u is within 30dBZ and 50dBZ. For liquid particles, DFR is positive or negative, but generally smaller than solid and mixed particles, and Z_eK_u is within 30dBZ and 50dBZ. When Z_eK_u is within 30dBZ and 40dBZ, solid and mixed particles are slightly overlapped. Overall, on the Z_eK_u -DFR plane, particles with three phases of stratiform precipitation can be separated well, although they are overlapped slightly. According to Figure 1b, for convective precipitation, Z_eK_u and DFR of solid and liquid particles have a positive correlation. For solid particles, DFR is within 3dBZ and 7dBZ. For liquid particles, DFR is within 1dBZ and 8dBZ. Compared to stratiform precipitation, Z_eK_u and DFR of convective precipitation are relatively larger. There is not overlapped area due to non-existence of mixed particles, so that the two phases of particles can be separated completely. According to the theoretical simulation results of T matrix, this paper respectively recognizes particle phase of stratiform precipitation and convective precipitation with KNN algorithm. When KNN model is created, 50% of the simulation results are used for training and the rest 50% results are used for test. The solid and liquid particles of convective precipitation are slightly overlapped on the Z_eK_u -DFR plane, for which KNN model can recognize basically with an accuracy rate up to 99%. In addition, the mixed particles of stratiform precipitation are partially overlapped with other particles on the Z_eK_u-DFR plane, for which KNN model can recognize with an accuracy rate 91%, lower than the convective precipitation.

From the view of scattering characteristics of precipitation particles, this paper simulates the reflectivity factor and DFR of particles in different phases of different precipitation types at Ku and Ka band by the T-matrix method; analyzes the feasibility of recognizing particle phase at the two bands of DPR; then trains KNN algorithm based on the simulation results for different precipitation types by the T-matrix method and uses the trained KNN algorithm for phase recognition. Conclusions are drawn as below:

A. According to the simulation results based on the T-matrix method, for stratiform precipitation, different phases of particles are slightly overlapped on the Z_eK_u -DFR plane, where omission in phase recognition can occur. For convective precipitation, different phases of particles can be separated highly due to non-existence of mixed particles.
B. Based on the simulation results by the T-matrix method, the particle phase can be recognized with KNN algorithm, with an accuracy rate up to 91% for stratiform precipitation and 99% for convective precipitation.

1. Cheng Z, Liu X, Zhu Y (2009) A process of hydrometeor phase change with dual-polarimetric radar. Journal of Applied Meteorological Science 020(005): 594-601.
2. Wu Q, Yang M, Dou F (2017) Study of GPM dual-frequency radar in detecting snow. Meteorological Monthly 43(3): 348-353.
3. Le M, Chandrasekar V, Biswas S (2017) An algorithm to identify surface snowfall from GPM DPR observations. IEEE Transactions on Geoscience and Remote Sensing 55(7): 4059-4071.
4. Li L, Guan L (2020) Surface snowfall identification algorithm based on GPM-DPR observations. Progress in Geophysics 35(1): 23-31.
5. Liao L, Meneghini R (2011) A study on the feasibility of dual-wavelength radar for identification of hydrometeor phases. Journal of Applied Meteorology & Climatology 50(2): 449-456.
6. Waterman P (1971) Symmetry, unitarity, and geometry in electromagnetic scattering. Physical Review D 3(4): 825.
7. Mishchenko M, Mackowski D, Travis L (1996) T-matrix computations of light scattering by non-spherical particles a review. Journal of Quantitative Spectroscopy & Radiative Transfer 55(5): 535-575.
8. Yang T, Yuan Z (2017) Simulation research on hydrometeor classification by multi-wavelength dual linear polarization doppler radar. Plateau Meteorology 036(001): 241-255.
9. Cover T, Hart P (1953) Nearest neighbor pattern classification. IEEE Trans Inf Theory 13(1): 21-27.
10. Chen X, Liu X (2019) Combining GPM DPR with s-band radar to retrieve RSD. Acta Scientiarum Naturalium Universitatis Pekinensis 055(002): 227-236.
11. Liebe H, Hufford G, Manabe T (1991) A model for the complex permittivity of water at frequencies below 1THz. International Journal of Infrared and Millimeter Waves 12(7): 659-675.
12. Zhang H, Zhang Y, Qie X (1999) Study on rainfall measurement and raindrop spectra with the differential reflectivity ZDR technique of a dual linear polarization radar. Acta Meteorologica Sinica 13(1): 115-128.