- Submissions

Full Text
Novel Research in Sciences
Artificial Neural Networks: Basic Methods and Applications in Finance, Management and Decision Making, a Roadmap
Papadopoulos T*, Kosmas IJ and Michalakelis C
Department of Telematics and Informatics, Harokopio University of Athens, Greece
*Corresponding author:Papadopoulos T, Department of Telematics and Informatics, Harokopio University of Athens, Greece
Submission: March 08, 2021;Published: March 22, 2021
.jpg)
Volume6 Issue5March, 2021
Abstract
Artificial Neural Network models have helped researchers to foresee the outcome of problems in many scientific fields. These models are presumed as a computer-based stimulation of the human neural system capable to benchmark values. They employ functions among a large variety of data examples driving to knowledge, identify relationships or errors and finally provide a possible outcome. From a decisionmaking perspective the Neural Network approach is very helpful even if it is difficult to implement it in real cases. Recently they are increasingly applied in many fields of science such as finance, strategic and project management and business policy implementing forecasts, pattern recognition and predictions using historical data. This study is an overview of the basic models of Artificial Neural Networks, as much as a literature review used in specific fields of science. The goal of this study is to serve as a roadmap for an early researcher to understand the principles of Artificial Neural Network models and the underlying mathematics, to become familiar with their applications over certain areas and to guide further exploration of this area.
Keywords: Neural networks; Decision making; Finance; Science; Humans; Nucleus; Nerve
Introduction
The concept of simulating a thinking machine was introduced by Alan Turing in 1950,
who proposed that if a computer-human interaction seems like human-human interaction
then we should consider the computer in question to be intelligent. Generally, Artificial
Intelligence systems act like humans, meaning that they need to access and use knowledge in
order to solve problems by applying conditions, logic, hunches and intuition in order to make
a decision [1]. Neural network methods are inspired by biology with analogous components
of living organisms. While in biological Neural Networks dendrites collect signals and send a
signal through an axon which in turn connects it with neurons which are excited of inhibited as
a result, in Artificial Neural Networks input data are sent to a processing entity (simulating a
neuron) which in turn sends output signals to other entities [2]. Such signals mainly follow the
form of an “if-then” rule where Neural Networks analyze large number of variables identifying
inter-actions and patterns [3], discovering rules and learning. Compared to other statistical
models, Artificial Neural Networks constitute a better approach to deduce assumptions based
on independent data [4,5]. Neural networks help to identify patterns among computer files,
requiring assumptions and to organize and classify data achieving satisfactory predictions.
These characteristics can make them a useful tool in finance [6], management [7], decisionmaking
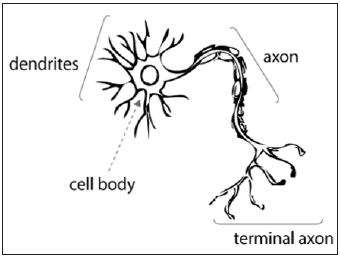
and strategic planning [8]. As demonstrated in (Figure 1):
a. The nerve cell consists of the body.
b. The body of the nerve cell also contains the nucleus.
c. Dendrites are many and short.
d. The axon is one and long.
e. The main functional feature of the nerve cell is that when it receives a stimulus it is
activated.
The human brain, an extremely large, interconnected network of neurons, models the
planet around us, as depicted in (Figure 1). A neuron collects input from other neurons using dendrites. It then summates the inputs and when the resulting
value is higher than a threshold then an appropriate signal appears.
This signal is finally sent to other connected neurons through
the axon. Neural network algorithms are considered among the
foremost powerful and widely used ones. In a macroscopic point
of view, they could appear as a blind box: There is an input layer
which transmits info to the “hidden layer(s)” which subsequently
implements calculations to send results to the output layer. In
order to implement and optimize a neural network it is crucial to
understand how hidden layers operate. When a nerve cell is affected
by a stimulus (E.g., electrical stimulation), then the membrane is
potentially inverted. In other words, when under the influence
of a stimulus the nerve cell is activated, the negative membrane
loads move outwards and the positive inwards. But what was the
problem-solving process before the development of the Neural
Networks?
Figure 1:Human brain neural network.
a. Before Neural Networks, computers solved problems
following specific commands provided by programmers.
The capability to solve problems was limited to those that is
possible to provide a list of commands.
b. Unfortunately, many real-world problems are very
complex, have no analytical solution and require alternative
approaches, as for example heuristics. For instance, imagine
that someone wants to recognize a handwritten letter.
c. It is practically impossible to describe (in programming
language) how a letter may look like as different people write
letters with different handwriting.
On the other hand, in order to digitally read handwritten letters, it is more helpful to use algorithms that recognize patterns through examples. The idea is to create a machine which will potentially be able to recognize patterns while its programmer probably would never understand the pattern itself. This means that a great number of different handwritten letters could be recognized discerning similarities and differences. Therefore, the aim of this work is to shed light on some applications of Artificial Neural Networks to forecast indicators used in specific fields, mainly finance, management and decision-making. Arguably, researchers as well as practitioners could use this study as an example of methodology in order to implement forecasting using artificial neural networks, in domains like the ones described above. Future researchers will not only find in the present article the basic introductory elements for understanding Neural Networks, but they will also be inspired to engage in further research in these or other research areas. The rest of the paper consists of a literature review and history of the artificial neural networks, including some significant milestones (section 2). After this review follows a short introduction to the basic Artificial Neural Network Models (section 3) and their applications to selected areas (section 4). Finally, section 5 includes an analysis of the models’ performance and section 6 concludes.
Literature
Kitcenham & Bereton [9] list three important reasons for
conducting a literature review on information engineering and IT:
1. summarizing empirical facts, the advantages and disadvantages
of a given technology, 2. to recognize any existing gaps in and
recommend further research; and 3. to include a basis for the correct
deployment of future study activities. This study is consistent with
the second purpose, with the goal of shedding light on some of
the applications of Artificial Neural Networks in different fields,
especially economics, management and decision-making and also
recognize gaps in these areas. Authors started the automated
research in several databases (google scholar etc) reviewing all
relevant studies (journals, conference, books etc). At the same time
authors considered inclusion and exclusion criteria in order to reach
the final insight. The key words that have been used for the present
paper are: “Neural Networks application in management”, “Neural
Networks application in decision making”, “Neural Networks
application project management”, “Neural Networks application
in finance”. The development of artificial neural networks has a
noteworthy history. This study presents some major events and
achievements during their evolution, in order to underline how
research developed until now. In 1943, for the first time, Culloch
& Pitts [10] proposed the idea of data processing through binary
input elements, called “neurons”. These networks differ from those
in the conventional computer science, in the sense that the steps
of the programming process aren’t executed sequentially, but in
parallel with “neurons” [10]. It was said that the model became the
muse for deeper research.
In 1949, Donald Hebb [11] proposed algorithms that achieve
learning by updating neurons’ connections [11]. McCulloch and
Hebb contributed significantly to the development of neural
sciences studies [10,11]. In 1954, Minsky [12] built and tested,
the primary neurocomputer [12] and in 1958 Frank Rosenblatt
[13] developed the Perceptron as an element instead of a neuron
[13]. This was a trainable computer that could learn by changing
the connections to the edge components and therefore identify
patterns. The theory motivated scientists and became the basis for
the essential algorithms of machine learning. This innovation led to
the establishment of a public company for neural networks in 1960
[14]. Nils Nilsson [15] monograph on learning algorithms outlined
any research development done so far [15] and any drawbacks found in learning algorithms. Sun Ichi Amari [16,17], Fukushima [18] and
Miyaka (1980) discussed further the threshold components and the
statistical principles of neural networks. Associative memory has
further been reviewed by Tuevo Kohonen [19-25]. Later surveys
in neural networking took into consideration Hopfield’s model
as most appropriate for very large-scale integration designs [26]
improved layered models [27]. The variety of applications where
neural networks could be used has radically been increased from
tiny examples to broad cognitive activities. Nowadays, scientists
and practitioners develop complicated interconnected neural
network chips of large scale. There is much research to be made in
order to understand neural networks deeply and therefore achieve
better results but there is still a satisfactory number of models
ready to be issued to solve many problems.
Basic Artificial Neural Network Models
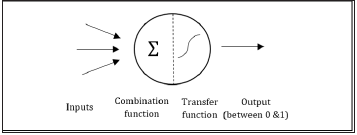
Neural Network models are suitable to solve prediction and forecasting problems that have the following characteristics: i. the input is well understood, ii. the output is well understood and iii. experience is available [28]. These models consist of an input layer of neurons that sends signals to a hidden middle layer. The hidden layer of neurons computes weights and sends them to the output layer which aggregates data and generates the final output [2]. These models can classify outcomes [29] and identify patterns [30]. The procedure contains data to be fed and then processed within the layers. The structure described above is illustrated in (Figure 2). Having similar behavior to biological neurons, nodes combine inputs though an activation function to produce signal to the output layer. Each input has a different weight, which is acquired by training, taking into consideration the contribution or importance of each variable [4]. This function consists of two basic parts: i. a combination function that merges all input values to one and ii. a transfer function which produces the final outcome. A linear transfer function does not answer to most cases while sigmoid and hyperbolic tangents functions work better mainly because they can block function results between 0 and 1 (Figure 3).
Figure 2: The structure of a neural network.
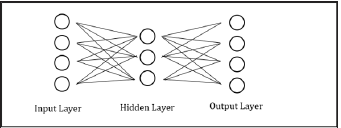
Figure 3:Activation and transfer function.
Simple feedforward neural networks
Feedforward Neural Networks use the supervised learning method [31] which implements the learning process by specifying the desired output for every pattern encountered during training and by treating to differences between the network and training target as errors to be minimized [32]. The Perceptron is a simple topology of feedforward Neural Network without hidden layers. It is the first network introduced by Rosenblatt [13] in 1958 as a mechanism that is able to be trained in classification of models [33]. In the perceptron model, learning is an error-driven process calculating weights given a binary input vector to calculate output. The Perceptron learning algorithm has the following steps which are repeated until weights stop changing much:
i. For each x-> (input) and t-> (desired output) calculate y-> (output).
iii. If x-> ≠ t->
x-> =t-> then add to every weight that has xi ≠ 0 , the difference Δw = d (t − y) , (d is the learning rate).
A generalization of the Perceptron model is the Delta Rule learning algorithm that was introduced by Widrow & Hoff [14]. It is also an error driven learning algorithm, like Perceptron, with the difference that in order to stop the algorithm the mean square error of the input vector should be minimized. Given a p -> learning vector the mean square error is calculated by the function:
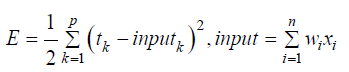
In Delta Rule weights in the algorithm change by the following quantity:

Although Delta Rule learning algorithm is an improved version of the Perceptron model it cannot be used to Neural Networks with hidden layers because it is difficult to calculate the target output value tk of each hidden node [33].
Backpropagation model
A highly successful and widely used [34] feedforward training model is backpropagation model (Figure 2), which identifies relationships between variables (inputs and outputs) [35]. The backpropagation model employs feedforward functions among a large variety of data examples driving to knowledge [36], it identifies relationships and errors and finally provides a possible outcome. Its algorithm drives the model to a learning procedure using trials and errors in order to determine the available correct answers [37]. It consists of two propagations: The forward pass, meaning the data imported to the input layer and the backward pass, meaning the feedback received and network response through error-correction knowledge [38]. The backpropagation algorithm begins the learning process using input vectors from past datasets. At first the model is initialized to small random values [39]. Each node of the input layer produces -through the transfer function- its own output which is considered as an input value to next hidden layer nodes. This continues to every hidden layer until it reaches the output layer which produces the final output value of the network. The input value of the j hidden, or output layer node is calculated by the function:
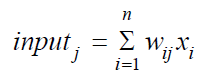
The output value of this node is calculated from the transfer function:
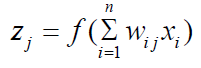
During the learning process for each input vector from past data the desired outcome is known. Using Delta Rule to the k output layer weights change:
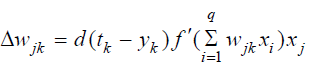
Where d is the learning rate.
When the calculation of new weights to the output layer is
complete the value 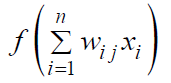 is now considered as desired output
values to the first from the end hidden layer and then all weights
are calculated using the same algorithm backwards until all weights
change. This is a gradient descent optimization procedure which
minimizes the mean square error E between output and desired
output [40]:
is now considered as desired output
values to the first from the end hidden layer and then all weights
are calculated using the same algorithm backwards until all weights
change. This is a gradient descent optimization procedure which
minimizes the mean square error E between output and desired
output [40]:
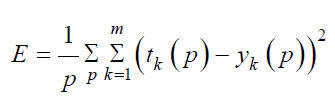
Hopfield model and bidirectional Associative Memories (BAM)
The innovation that Hopfield Networks [41] brought in 1982 was the introduction of the energy function which describes the situation of the network; like in thermodynamics, where the system tends to minimize its energy. Its topology consists of one layer in which every node is connected with every other with two-way connections and symmetric weights. In the Hopfield model every j node takes as input value the initial j input from the input vector as well as the sum of output values of every other i≠j node.
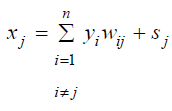
where xj is the input to j node, yi is the output of the other i
nodes and sj is the input value.
In the Hopfield model weights table during learning process is
easily calculated:

Where Sk = (Sk1, Sk2 ,..., Skn ) and wij = 0
when i = j
Nodes are simple Perceptrons with the following activation
function:

Where yj’ is the output of the previous learning season of the
learning algorithm.
The Hopfield Algorithm ends when energy function converges
in a steady state:
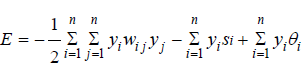
Kosko introduced in 1988 an extension to Hopfield model, the Bidirectional Associative Memories (BAM) which has one more layer (two layers). The weight table during learning process in this model is:
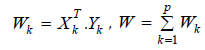
The energy function for BAM model is simpler than Hopfield’s:
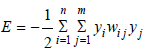
Kohonen network model
Kohonen model differs from the others as it consists of many neurons placed in a geometric topology like straight line, plane, sphere etc. Each neuron is connected with the input layer receiving every input vector. During the learning process the network separates neurons into categories matching input values to a neuron which affects its nearby neurons. Neurons in the neighborhood strengthen their output values while others weaken them. Given a S = (S1, S2 ,..., Sn ) input vector the learning process calculates the distance between vectors S and wi , where wi = (wi1, wi2 ,..., wik )
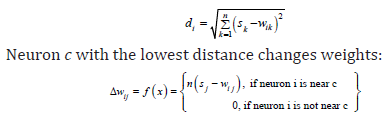
where n is the learning rate.
Applications of Neural Networks
Neural Network models can be utilized in several domains. Potential applications of Neural Network in finance may be the estimation of stock market and currency values (i.e., forecasting) or the analysis of strength of historical (or pro forma) financial statements (i.e., classification). Chase Manhattan Bank, Peat Marwick, American Express are between the most well-known companies that efficiently apply Neural Networks to solve problems in finance and portfolio management [42]. In 1998, O Leary [43] analyzed studies that presented that artificial neural networks could be used to foresee the failure or bankruptcy of companies. He proposed plenty of data details for each analysis in order to substantiate his claims. Key factors that may affect the outcome of these predictions are the type of the model and the software that is used (means of development) as well as the complete structure of nodes (input, secret and output layers). Zhang et al. [44] reviewed 21 papers addressing neural network models with simulation issues to forecast values and 11 more with studies comparing neural models’ performance with conventional statistical approaches. According to them, the modeling problems are the kind of knowledge, the number of available data for the learning procedure, the model design (how many nodes and layers form the neural model and what transfer function is used), the specific algorithm and the normalization process. It’s widely accepted that artificial neural networks’ financial systems are included in many studies [45- 47]. Foreign exchange rates, stock values, credit risk and business failures are widely estimated by neural network models [48-56]. Considering that a manager in daily basis is required to make many decisions, it is of great importance to ensure that will make the right ones [57]. For example, in the case of deciding whether to introduce a new product in an industry or not a neural network model may provide real-time estimations with high level accuracy. The findings are tested by utilizing data on the life cycle of the item. For example, it is proved that the engine rpm (revolutions per minute), the winding temperature and the strength are sometimes used to predict the remaining life of a component [58].
In decision‐making, researchers argue that political decisions can be assisted by Neural Network models as well. Politicians have to make thousands of decisions during their governance. Some of them, can rise them to the top of publicity while some others can drive them straight to the bottom and of course to end up losing the elections. An imaginary application which could process every data throughout the world, could potentially foresee the outcome of future elections considering how voters may respond to international or national matters [59]. Regarding funding investments, scarce resources force decision makers to decide which projects will get funding and which will not. Unfortunately, it is very hard to develop a reliable framework for such an evaluation [60] especially to projects that may be affected by complex external conditions like migration and international protection management [61]. This decision is difficult because there are many uncertain economic, financial and social indicators that can simultaneously affect the cost benefit analysis of the project [62]. This analysis will determine the Net Present Value of an investment which can help decision makers [63] to choose which project to finance within alternatives. This method gives monetary values to all positive and negative effects focusing in measuring and quantifying indirect effects [64].
Given the complexity of indicators, a powerful branch of artificial intelligence, such as Artificial Neural Networks (Mavaahebi and Nagasaka, 2013), can be utilized to understand patterns [65,66] and forecast indicators in project management. In addition, neural models may be applicable to measure specific critical success factors serving as fundamental criteria to prevent failures [67]. In recent decades, artificial neural network models have helped researchers to foresee the outcome of such indicators [68], provide better decisions and therefore achieve high welfare to community and its citizens [69]. This analysis takes into consideration much uncertain information that increase the risk to make false predictions.
Conclusion
Artificial Neural Network models have helped researchers to foresee outcomes in many fields of science. These models are considered as a computer-based processor that learns from experimental data and makes analogous decisions [68] stimulating human neural. From a decision-makers perspective the Neural Network approach is very helpful even it is difficult to implement it in real cases [69-74]. Aiming at the characteristics of Artificial Neural Networks this study provided the basic models for Machine Learning and some of its applications in finance, management, project management and decision making [75-79]. Most models have common characteristics and prerequisites like the fact that their inputs and outputs should be well understood and that there should be much experience available. There is plenty of available studies and reviews describing how every field of science can utilize each model [80-83]. The scope of this study was not to present each separate model in detail but to provide directions and principles so that an early researcher can find a roadmap for deeper studying.
References
- Carling A (1992) Introducing neural networks. Sigma Press, UK, pp. 1-338.
- Garson GD (1998) Neural networks an introductory guide for social scientists. Sage Publications, UK, pp. 1-194.
- Chen CH (1996) Fuzzy logic and neural network handbook. McGraw-Hill, USA, pp. 1-700.
- Pradhana B, Leeb S, Buchroithnera MF (2010) A GIS-based back-propagation neural network model and its cross-application and validation for landslide susceptibility analyses. Computers, Environment and Urban Systems 34(3): 216-235.
- Lacher R, Coats P, Shanker C, Franklin L (1995) A neural network for classifying the financial health of a firm. European Journal of Operational Research 85(1): 53-65.
- Wong K, Selvi Y (1998) Neural network applications in finance: A review and analysis of literature (1990-1996). Information & Management 34(3): 129-139.
- Sharma A, Chopra A (2013) Artificial neural networks: Applications in management. Journal of Business and Management 12(5): 32-40.
- Dunke F, Nickel S (2020) Neural networks for the metamodeling of simulation models with online decision making. Simulation Modelling Practice and Theory 99: 1-18.
- Kitchenham B, Brereton P (2013) A systematic review of systematic review process research in software engineering. Information and Software Technology 55(12): 2049-2075.
- McCulloch W S, Pitts W (1943) A statistical consequence of the logical calculus of nervous nets. Bulletin of Mathematical Biology 5(4):135-137.
- Hebb DO (1949) The organisation of behaviour. John Wiley & Sons, USA, pp. 231-337.
- Minsky M (1954) Neural nets and the brain-problem model doctoral dissertation.
- Rosenblatt F (1958) The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review 65(6): 386-408.
- Widrow B, Hoff ME (1960) Adaptive switching circuits. Ire Wescon Convention Record, USA, pp. 96-104.
- Nilsson N (1965) Learning machines. McGraw-Hill book Company, USA.
- Amari SI (1972) Characteristics of random nets of analog neuron-like elements. IEEE Trans on Syst Man and Cybernetics SMC 2(5): 643-657.
- Amari SI (1977) Dynamics of pattern formation in lateral-inhibition type neural fields. Biological Cybernetics 27: 77-87.
- Fukushima K (1980) Neocognitron: A self-organizing neural network model for a mechanism of visual pattern recognition unaffected by shift in position. Bio Cybern 36(4): 193-202.
- Kohonen T (1977) Cluster analysis. Heineman Educational Books, UK.
- Kohonen T (1982) Self-organized formation of topologically correct feature maps. Biological Cybernetics 43(1): 59-69.
- Kohonen T (1987) Adaptive, associative, and self-organizing functions in neural computing. Applied Optics 26(23): 4910-4918.
- Kohonen T (2001) Self-organizing maps of massive databases. International Journal of Engineering Intelligent Systems for Electrical Engineering and Communications 9(4):179-186.
- Anderson JA, Silverstein JW, Ritz SA, Jones RS (1977) Distinctive features, categorical perception, and probability learning: Some applications of a neural model. Psychological Review 84(5): 413-451.
- Carpenter GA, Grossberg S (1987) A massively parallel architecture for a self-organizing neural pattern recognition machine. Computer Vision, Graphics, and Image Processing 37(1): 54-115.
- Carpenter GA, Grossberg S (1988) The ART of adaptive pattern recognition by a self-organizing neural network. Computer 21(3): 77-88.
- Zamani MS, Mehdipur F (1999) An efficient method for placement of VLSI designs with Kohonen map. IJCNN'99 International Joint Conference on Neural Networks, USA.
- McClelland JL, Rumelhart DE (1986) Parallel distributed processing: Explorations in the microstructure of cognition. In: Psychological and Biological Models, MIT Press, USA, pp. 1-547.
- Berry JAM, Linoff G (2011) Data mining techniques: For marketing, sales and customer relationship management. In: Wiley Computer Publishing, USA, pp. 1-888.
- Maulenkamp F, Grima MA (1999) Application of neural networks for the prediction of the Unconfined Compressive Strength (UCS) from Equotip hardness. International Journal of Rock Mechanics and Mining Sciences 36(1): 29-39.
- Dayhoff J (1990) Neural network architectures-An introduction. (1st edn), VNR-Van Nostrand Reinhold Company, USA, pp. 1-259.
- Japkowicz N (2001) Supervised versus unsupervised binary-learning by feedforward neural networks. Machine Learning 42: 97-122.
- Reed RD, Marks RJ (1999) Neural smithing-Supervised learning in feedforward artificial neural networks. MIT Press, UK, pp. 1-360.
- Vlachavas I, Kefalas P, Vasiliadis N, Kokkoras F, Sakelariou I (2011) Artificial intelligence.
- Mohammed EH, Sudhakarb KV (2002) ANN back-propagation prediction model for fracture toughness in microalloy steel. International Journal of Fatigue 24(9): 1003-1010.
- Davis JT, Massey AP, Lovel R (1997) Supporting a complex audit judgment task: An expert network approach. European Journal of Operational Research 103(2): 350-372.
- Hornick K, Stinchcombe M, White M (1989) Multilayer feedforward networks are universal approximators. Neural Networks 2(5): 359-366.
- Yu XH, Chen GA, Cheng SX (1995) Dynamic learning rate optimization of the backpropagation algorithm. IEEE Transactions on Neural Networks 6(3): 669-677.
- Ramamoorti S, Bailey A, Traver R (1999) Risk assessment in internet auditing: A neural network approach. International Journal of Intelligent Systems in Accounting, Finance and Management 8(3): 159-180.
- Gallant SI (1993) Neural network learning and expert systems. MIT Press, UK, pp. 1-382.
- Jian BJ, Guo YS, Hu CH, Wu LW, Yau HT (2020) Prediction of simple thermal deformation and displacement using back propagation neural network. Sensors and Materials 32(1): 431-445.
- Hopfield JJ (1982) Neural networks and physical systems with emergent collective computational properties. Proceedings of the National Academy of Sciences of the USA 79(8): 2554-2558.
- Maditinos D, Chatzoglou P (2004) The use of neural networks in forecasting. Review of Economic Sciences 6: 161-176.
- O Leary D (1998) Using neural networks to predict corporate failure. International Journal of Intelligent Systems in Accounting, Finance and Management 7(3): 187-197.
- Zhang G, Patuwo B, Hu Y (1998) Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting 14(1): 35-62.
- Trippi RR, Turban E (1993) Neural networks in finance and investment: Using artificial intelligence to improve real-world performance. (2nd), Irwin Professional Publishers, USA, pp. 1-821.
- Refenes AN (1995) Neural networks in the capital markets. John Wiley, USA.
- Gately E (1996) Neural networks for financial forecasting. (1st), Wiley, USA, pp. 1-169.
- Yu L, Wang S, Lai KK (2008) Credit risk assessment with a multistage neural network ensemble learning approach. Expert Systems with Applications 34(2): 1434-1444.
- Alfaro E, García N, Gámez M, Elizondo D (2008) Bankruptcy forecasting: An empirical comparison of AdaBoost and neural networks. Decision Support Systems 45(1): 110-122.
- Angelini E, Tollo G, Roli A (2008) A neural network approach for credit risk evaluation. The Quarterly Review of Economics and Finance 48(4): 733-755.
- Lee K, Booth D, Alam P (2005) A comparison of supervised and unsupervised neural networks in predicting bankruptcy of Korean firms. Expert Systems with Applications 29(1): 1-16.
- Baek J, Cho S (2003) Bankruptcy prediction for credit risk using an auto-associative neural network in Korean firms. Computational Intelligence for Financial Engineering. Proceedings, IEEE International Conference, pp. 25-29.
- Hann TH, Steurer E (1996) Much ado about nothing? Exchange rate forecasting: Neural networks vs. linear models using monthly and weekly data. Neurocomputing 10(4): 323-339.
- Borisov AN, Pavlov VA (1995) Prediction of a continuous function with the aid of neural networks. Automatic Control and Computer Sciences 29(5): 39-50.
- Grudnitski G, Osburn L (1993) Forecasting S and P and gold futures prices: An application of neural networks. The Journal of Futures Markets 13(6): 631-643.
- Bergerson K, Wunsch DC (1991) A commodity trading model based on a neural network-expert system hybrid. In: Proceedings of the IEEE International Conference on Neural Networks, US, pp. 1289-1293.
- Kosmas I, Dimitropoulos P (2014) Activity based costing in public sport organizations: Evidence from Greece. Research Journal of Business Management 8(2): 130-138.
- Mazhar M, Kara S, Kaebernick H (2007) Remaining life estimation of used components in consumer products: Life cycle data analysis by Weibull and artificial neural networks. Journal of Operations Management 25(6): 1184-1193.
- Khashman Z, Khashman A (2016) Anticipation of political party voting using artificial intelligence. Procedia Computer Science 102: 611-616.
- Sward D (2006) Measuring the business value of information technology: Practical strategies for it and business managers. Intel Press, USA, pp. 1-282.
- Papadopoulos T (2017) Managing Refugee crisis in Greece: Risk management in international protection funds. 3rd Conference of Department of Political Sciences and International Relations, University of Peloponnese, Greece.
- Dowd PA (1995) Risk assessment in reserve estimation and open-pit planning. International Journal of Rock Mechanics and Mining Sciences and Geomechanics 32(4): 148-154.
- European Union (2015) Guide to cost benefit analysis of investment projects. Economic appraisal tool for cohesion policy 2014-2020, EU Publications Office, Europe, pp. 1-364.
- Reynolds T (2009) The role of communication infrastructure investment in economic recovery. OECD Digital Economy Papers, France, pp. 1-39.
- Haykin S (2008) Neural networks and learning machines: A comprehensive foundation. (3rd edn), Pearson publisher, UK, pp. 1-936.
- Anderson J (1983) A spreading activation theory of memory. Journal of Verbal Learning and Verbal Behavior 22(3): 261-295.
- Costantino F, Gravio GD, Nonino F (2015) Project selection in project portfolio management: An artificial neural network model based on critical success factors. International Journal of Project Management 33(8): 1744-1754.
- Cheung SO, Wong PSP, Fung ASY, Coffey WV (2006) Predicting project performance through neural networks. International Journal of Project Management 24(3): 207-215.
- Papadopoulos T (2019) New techniques for the evaluation of projects may improve the impact of EU Funds (Case Study: Artificial Neural Networks). International Conference on the Impact of EU Structural Funds on Greece (1981-2019): Successes, Failures, Lessons learned and Comparisons with other EU members, University of the Peloponnese, Greece.
- Allen F, Myers S, Brealy R (2016) Principles of corporate finance. (13th edn), McGraw-Hill Companies, USA.
- Baye M, Prince J (2013) Managerial economics and business strategy. (9th edn), McGraw-Hill, USA.
- Bloom J (2005) Market segmentation: A neural network application. Ann Tour Res 32(1): 93-111.
- Cuadros A, Domínguez V (2014) Customer segmentation model based on value generation for marketing strategies formulation. Estudios Gerenciales 30(130): 25-30.
- Fish K, Barnes J, Aiken M (1995) Assistant, artificial neural networks: Anew methodology for industrial market segmentation. Ind Mark Manag 24: 431-438.
- Henseler J (1995) Back propagation-artificial neural networks: An introduction to Ann theory and practice. In: Braspenning PJ, Thuijsman F,Weijters AJMM, (Eds.), Springer, USA.
- Hopfield JJ (1984) Neurons with graded response have collective computational properties like those of two-state neurons. Proceedings of the National Academy of Sciences of the USA 81(10): 3088-3092.
- JiÍí T (2010) Application of neural networks in finance. Journal of Applied Mathematics 3(3): 269-277.
- Khare S, Gajbhiye A (2013) Literature review on application of artificial neural network (Ann) in operation of reservoirs. International Journal of Computational Engineering Research 3(6): 1-6.
- Maltarollo VG, Honório KM, Da Silva ABF (2013) Applications of artificial neural networks in chemical problems. In: Suzuki K (Ed.), Artificial Neural Networks-Architectures and Applications. InTech Publisher, UK, pp. 204-223.
- McCulloch S, Pitts W (1942) A logical calculus of ideas immanent in nervous activity. The Bulletin of Mathematical Biophysics 5:115-133.
- Amari SI (1972) Learning patterns and pattern sequences by self-organizing nets of threshold elements. IEEE Trans Computers C 21(11): 1197-1206.
- Tkáč M, Verner R (2016) Artificial neural networks in business: Two decades of research. Applied Soft Computing 38: 788-804.
- Zhang P, Qi M (2002) Predicting consumer business; techniques and applications. Retail Sales Using Neural Networks, Neural Idea Group Publishing, USA, pp. 1-271.
© 2021 Papadopoulos T. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
 a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 







.jpg)






























 Editorial Board Registrations
Editorial Board Registrations Submit your Article
Submit your Article Refer a Friend
Refer a Friend Advertise With Us
Advertise With Us
.jpg)






.jpg)













.bmp)
.jpg)
.png)
.jpg)














.png)

.png)



.png)






