Nautical Solutions to Shipments for Internally Displaced Persons in Selected African Countries: A Profit Maximization Scenario

A Linear Programming Model is a mathematical optimization technique used to maximize or minimize a specific chosen objective function relative to some constraints to the decision variables. Bhattacharya [1] defines an optimization problem with a linear objective function and constraints as a linear programming problem, stating that a vector satisfying the inequality and non-negativity constraints is called a feasibility solution. This implies that if a linear programming problem and its dual have feasible solution, then both have optimal solutions, and the value is the same for both. However, if either the program or its dual does not have a feasible solution, then neither has an optimal vector. Hence the simple method is a common method of solving a linear programming problem.

On the other hand, Wikipedia defines an internally displaced person (IDP) as someone who is forced to flee his or her home but who remains within his or her country’s borders. They are often referred to as refugees, although they do not fall within the legal definitions of a refugee. They may be found in every continent of the world and in most countries of the world, especially where war, famine, ethnic and political disturbances as well as terrorism prevails. It is estimated that IDPs have a total population of 37.494 million and distributed as follows: the Middle East and North Africa is 13.933 million, Europe and North Asia – 2.804 million, Sub- Saharan Africa- 10.762 million, Asia and the Pacific- 2.879 million and Americans- 7.113 million. This total population rose to 67.7 million people in 2016.

As a result of the conflict in some parts of Africa, there have been growing concerns about food security in the continent. Famine, conflict, and drought have ravaged countries in West & East Africa. The United Nations Council passes a vote for the Food and Agricultural Organization (FAO) to step in and manage the crises. The FAO will intervene through the World Food Programme (WFP), a non-profit organization.

The WFP plans to provide humanitarian assistance first to the most affected countries which are most accessible namely: Nigeria, Sudan, Madagascar, Somalia and Namibia. The logistics of getting the relief materials from origin to destination at the best cost possible to the UN and relief agencies and a maximized profit for the shipping company who undertakes the herculean tasks of the nautical operations to supply the materials to the IDPs.

To this end, the critical question would be how could the supplies be made to the destinations in order to maximize the profit of the shipping line? This invariably would aid in addressing the specific objective of this paper which seeks to formulate a linear programming problem to optimize the profit of the shipping line.

Zangiabadi & Maleki [2] defines the concept of optimality for linear programming problems with fuzzy parameters with respect to the ones with multi objective linear programming problems, as they applied the concept of comparison of fuzzy numbers to transform a linear programming problem. Hence, they proposed several theorems which were used to attain optimality for linear programming problems with fuzzy parameters.

Alternatively, Juan & Xueqian [3] recognize linear programming as an important branch of operational research which is a mathematical method that assists in carrying out scientific management. They applied GAM-an advanced simulation and optimization modeling language which combines a large number of complex mathematical programming, such as linear programming, non- linear programming and mixed- integer programming with the system simulation to simulate and optimize investment decision- making of power generation to arrive at an optimal installed capacity of power plants and a final total cost; which provides the rational decision making basis for optimized investments.

Relatively, Singh, Varma & Kumar [4] formulated linear programming models to solve a management problem of staff training in a higher institution in India. They identified two categories of staff-junior and senior as the decision variables and using the available time for the training as the constraint equations; for both the administrative and academic departments to reveal the optimal cost of training and number of staff who ought to be trained respectively.

On the other hand, Akpan & Iwuok [5] applied the simplex algorithm to allocate raw materials to competing variables in a bakery in order to maximize profit of the firm. The results of the analysis reveal that 962 units of small loaf, 38 units of big loaf and 0 unit of giant loaf should be produced so as to attain a profit level of N20383. Sensitivity analyses reveal that small loaf and big loaf had to the profit hence suggesting their production for an optimized profit level of the firm.

The paper applies the Simplex method of linear programming (LP) to solve the formulated LP problem. The general formulation of the LP problem can be stated as follows [6]: In order to find the values of n decision variables X₁, X₂ …X_n to maximize or minimize the objective function. 

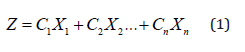
and also satisfy m – constraint 

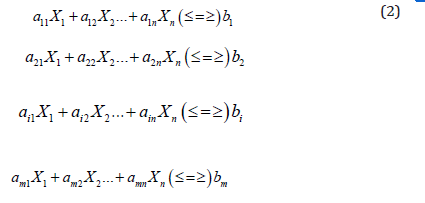
where constraints may be in the form of inequality ≤ or ≥ or even in the form of an equation (=) and finally satisfy the non-negative restrictions

Problem formulation

The WFP engages a leading shipping company registered in the United States of America for a one year contract for the carriage per shipload of relief materials delivered to the afore stated countries whereby the respective payments would be as follows at the end of the contract term:

Nigeria = $1,500,000 per completed delivery

Sudan = $1,650,000 per completed delivery

Madagascar = $1,820,000 per completed delivery

Somalia = $1,800,000 per completed delivery

Namibia = $1,600,000 per completed delivery.

The problem for this shipping Line would be the determination of which countries to ship to in order to make the most profit. How will she fulfill the contractual obligations while making the highest profit possible? Therefore, the shipping line needs to allocate its finite resources to the delivery of the relief materials to the various countries. The resource constraints for shipping line per shipload are taken as:

• Fuel Utilization
• Operating Cost (Crew Wage, Victuals, Stores, Repair & Maintenance, Admin, Insurance etc.)
• Voyage Cost (Port/Canal Charges, Services, Tug, Pilotage, Cargo Handling, Agents etc.).
• Depreciation (Ship Cost/Loan Repayment)

Hence, the company has to determine which countries to ship to and the frequency of service over the one-year period so as to determine the optimal profitability of the contract. The following assumptions would be made:

The shipping line has the following capacities, costs and budgets at the opening of each year;

• Fuel Purchase Budget = $5,000,000.
• A Handy Bulk Carrier of 30,000 DWT (TEU), 12,000 T displacement, making 15Knots at 35 T/day fuel consumption with day rate of $28,000 /day
• Shipping Cost Budget = $25,000/day
• Total Shipping Cost Budget = $5,000,000 per year.
• Depreciation = $2584/day
• Total Depreciation Costs Budgets = $1,000,000
• Vessel life span = 20years
• Exploitation per year =350days

This implies that the shipping line has made a fiscal year budget of $11,000,000 for fuel purchase, shipping costs and depreciation.

Depreciation

This is a Capital cost or decline in value of asset and allocation of the cost of tangible assets to period in which the assets are used. Depreciation depends on the cost of asset, expected salvage value of asset, estimated useful life of the asset and a method of appropriating the cost over such life and can be paid once or twice per year. Applying the Straight-line depreciation method, we have a value of $2584/day.

Fuel utilization

Table 1: Estimates of the distance between the ports using the closest sea route of the countries.

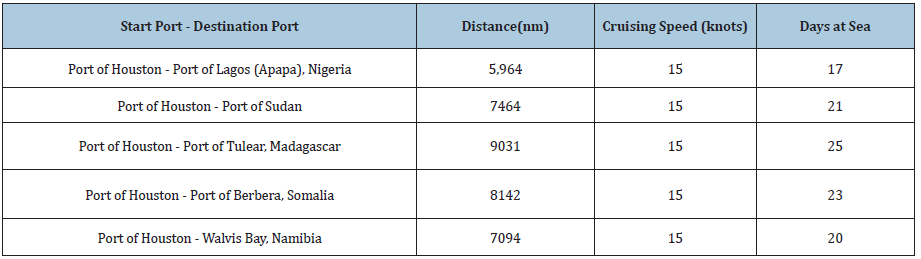
On average, a Handy Bulk ship can use up to 35 tons of fuel per day, which is around 9631 gallons. Using the information from the table above, the Bulker navigates at a speed of 15 knots, the fuel consumption for each trip to the various countries would be; (Table 1)

Houston – Nigeria = 595 tons of fuel

Houston – Sudan = 735 tons of fuel

Houston – Mali = 875 tons of fuel

Houston – Somalia = 805 tons of fuel

Houston – Libya = 700 tons of fuel

Given the fuel purchase budget of $5,000,000 and the market price of HFO at Houston Port is about $460/t, this implies that League Maritime Ltd will have a fuel use capacity of ($5,000,000/ $460/t) 10,869.56 tons per year, given the current market price of HFO.

Shipping cost budget

The shipping line provides each ship with a budget per trip to cover both operating costs and voyage costs. This amounts to $25,000 per day. From the distance between Houston and the receiving ports, we have the following shipping costs budget per trip; (Table 2)

Table 2: Estimated Shipping cost for the Countries.

Depreciation costs budget

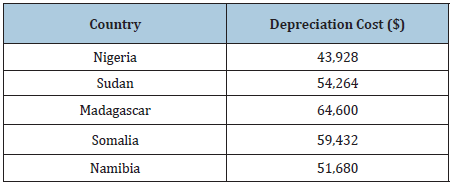
The shipping line has a depreciation cost of $2584/day when her Handy Bulk Carrier sails with cargo. She also has a total yearly budget of $1,000,000 set aside for depreciation/Loan repayments. Given the information of days at sea required by the Handy Bulk Carrier to reach the various destination ports from Houston, we can calculate the depreciation costs per trip as follows; (Table 3)

Table 3: Estimated Depreciation cost of ship on voyage to selected countries.

Model formulation

Model Formulation (Table 4)

The Decision Variables are defined in the following way:

Let Z = Profit per unit of Shipments payment

X1 = Amount of payment for Shipments to Nigeria per year

X2 = Amount of payment for Shipments to Sudan per year

X3 = Amount of payment for Shipments to Madagascar per year

X4 = Amount of payment for Shipments to Somalia per year

X5 = Amount of payment for Shipments to Namibia per year

The model is hence formulated as

Maximize Z = 1,500,000X1 + 1,650,000X2 +1,820,000X3 + 1,800,000X4 + 1,600,000X5

Table 4: The variables for Constraint equation.

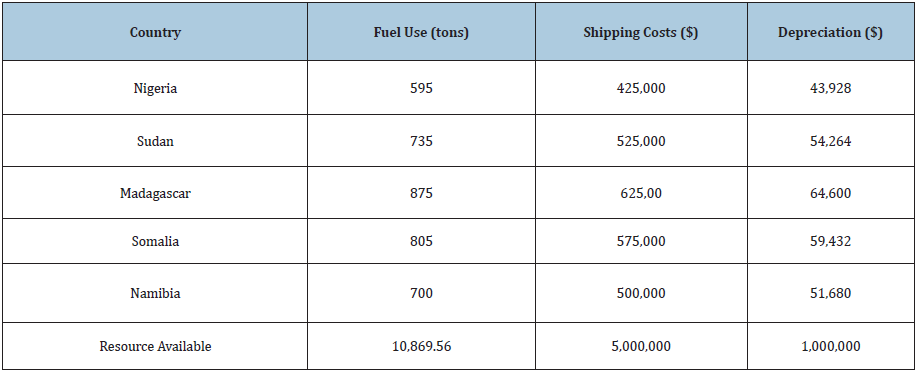
Subject to the following constraints:

• Fuel Utilization

595X1 + 735X2 + 875X3 + 805X4 + 700X5 ≤ 10,869.56

• Shipping Costs

425,000X1 + 525,000X2 + 625,000X3 + 575,000X4 + 500,000X5 ≤ 5,000,000

• Depreciation Costs

43,928X1 + 54,264X2 + 64,600X3 + 59,432X4 + 51,680X5 ≤ 1,000,000

Therefore, the Complete LP Model for League Maritime Ltd. would be written as;

Max Z = 1,500,000X1 + 1,650,000X2 + 1,820,000X3 + 1,800,000X4 + 1,600,000X5

Subject to:

595X1 + 735X2 + 875X3 + 805X4 + 700X5 ≤ 10,869.56

425,000X1 + 525,000X2 + 625,000X3 + 575,000X4 + 500,000X5 ≤ 5,000,000

43,928X1 + 54,264X2 + 64,600X3 + 59,432X4 + 51,680X5 ≤ 1,000,000

Where

Xi > 0, i= 1, 2,3,4,5.

The following results are obtained from the software computation to reveal the output as shown in Table 5.

Table 5: Data Output.

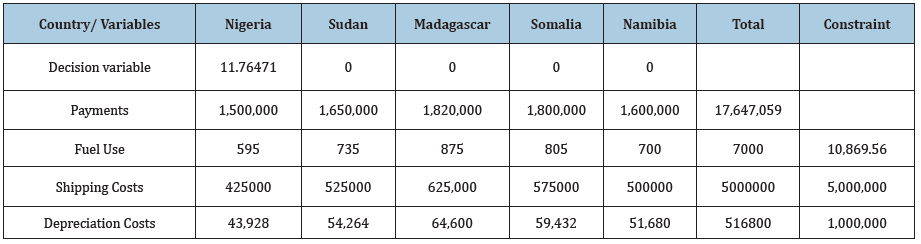
From the Linear Programming solution, the highest payments would be obtained from the contract if the shipping line were to make shipments only to Nigeria. The results further reveal that a shipment delivery of 11.764 times will result in a payment of $17,647,059 at a cost of;

Fuel Use: 7000tons * $460/ton = $3,220,000

Shipping Costs: $5,000,000

Depreciation Costs: $516,800

Total Shipping Cost: $8,736,800

Profit: $17,647,059 - $8,736,800 = $8,910,259.

The above results align with the findings of Sulemana and Haadi that derived an optimal profit for Bank X Tamale in Ghana from the formulation of linear programming problem of the bank taking into cognizance her financial transactions with her customers.

It could be deduced that this maritime company does not exceed her budgets for fuel, shipping costs and depreciation, she uses less than was actually budgeted for these cost components. It is recommend that the shipping line should go ahead to sign the contract with the World Food Programme for deliveries to Nigeria, this is because she would maximize her profit to about $8,910,259 in profits for the duration of the contract which is one year.

1. Bhattacharya RR (2016) Linear programming. In: Augier M, Teece DJ (Eds.) Palgrave Encyclopedia of strategic management UK.
2. Zangiabadi M, Maleki HR (2007) A method for solving Linear programming problems with fuzzy parameters based on multi objective linear programming technique. Asia Pacific Journal of Operations Research 24: 557-573.
3. Juan WU, Xuequian GE (2013) Optimization research of generation investment based on linear programming model. International Conference on Physics and Industrial Engineering. Physics Procedia 24: 1400-1405.
4. Singh RK, Varma SP, Kumar A (2013) Application of linear programming techniques in personnel management. IOSR Journal of Mathematics 8: 45-48.
5. Akpan NP, Iwok IA (2016) Application of linear programming for optimal use of raw materials in backery. Journal of Mathematics and Statistics Invention 4: 51-57.
6. Kalavathy S (2002) Operations research. (2^nd edn) Viskas Publishing House PVT LTD. New Delhi, India.