Geodesic Angle and Technology

Kinematic, dynamic and angular parameters are applied in the technology of rotational motions to describe their mechanism. A so-called geodesic angle (φ) identified based on the laws of differential geometry is important among them [1-3]. It is practically applied, for instance, in the technique of calculating the armoring of rotation shells when producing cylindrical bodies of spaceships [4,5].

Based on this technique the body cylindrical shell is armored along the geodesic line. “Geodesic line is the curve of certain type, generalization of the concept – straight line for curved spaces” [2]. On the circular cylinder these are screwed lines providing the shortest distance between the points on the surface of rotation.

If polymeric threads are wound onto the apparatus base along the geodesic line, the angle between the rotation axis and winding vector is the geodesic angle equaled to 54°44´=54,733° [4,5]. It is known that a silkworm uses the same angle when winding the natural viscose thread onto the base. The same principle is used in agricultural technology, for example, when winding linen threads onto the base. It is possible that this rule also works in microstructural processes, for instance, in the process of winding or unwinding DNA molecule spiral.

This investigation is targeted at revealing the physical sense of geodesic angle and analyzing the possibilities of its technical application.

Geodesic angle in the conformation of stable systems

Based on the analysis of the first law of thermodynamics the following was obtained [6]:

1. In the systems in which the interaction proceeds along the potential gradient (positive work), the resultant potential energy is found based on the principle of adding reciprocals of corresponding values of subsystems. This is the corpuscular process, in which entropy can serve as the theoretical concept.
2. In the systems in which the interactions proceed against the potential gradient (negative work) the algebraic addition of their masses, as well as the corresponding energies of subsystems is performed. This is the wave process, in which negentropy can serve as the theoretical concept.
3. The resonance stationary state of the systems is fulfilled under the condition of equality of degrees of their corpuscular and wave interactions. The entropy products in stationary state are completely compensated by the negentropy flow. Thus, “in the circular process in the thermal machine the system entropy increase due to the incoming heat is completely compensated by the entropy decrease during heat emission, and total entropy value equals zero” [7]:

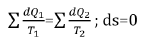
These rules are applied and revealed in many micro- and macroprocesses.

As applicable to corpuscular-wave processes, the condition of stationary state is the condition of equality of degrees of their structural interactions:

Mathematically and graphically (by nomograms) the stationary state in microsystems is found by the following equation:

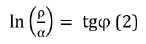
Where  – geodesic angle, relative difference of energy parameters of interacting systems.

Similarly, the equations for  are obtained:

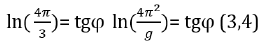
where g – free fall acceleration.

In [4;5] the notion of ultimate breaking stress during the thread plastics extension by its winding pitch is used: σ_α – axial, σ_β – circumferential stresses which are substituted by the proportional value N_α – axial “stress” and N_β – circumferential “stress”. At the same time, the following is fulfilled in the kinematics of mechanical systems:

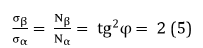
“This condition allows obtaining the equally stressed system of threads with the minimal product weight [4,5]”.

Similarly, for the gravitation mechanism and preserving the formalism of equations (2,5) we have [8]:

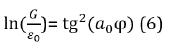
Where  – electric constant, G – gravitational constant,  – quantum correction to electron gyromagnetic ratio in an atom, which may, in this case, characterize the influence of particles motion precession.

Thus, the equality of corpuscular and wave interactions defines the resonance stationary state of the system. At the same time, the geodesic angle numerically defines the ratio of two legs of the right triangle whose values characterize energy dependencies through axial and circumferential stresses in the system with corpuscular-wave processes. This condition corresponds to the most optimal technological options and is widely present in nature, as well as in fractal systems.

Thus, thousands of years ago it was found: “All phenomena of the world around us, including a human and nature, are interpreted by Chinese medicine as the interaction between two origins “Yin” and “Yang” representing opposite aspects of unified reality” [9]. From the point of these notions physiotherapy and reflexotherapy can be considered as the technique for equalizing the potentials of two manifestations of energy origins, which, according to modern notions, are entropy and negentropy (par. 3 of the initial provisions).

Golden rules of Egyptian pyramids

“The proportions of Cheops Pyramid, cathedrals, bas-reliefs, household items and jewelry of the tombs testify that Egyptian craftsmen used the ratio of “golden section” when creating them” [10].

“Golden section” or “golden ratio” (Ф) – the ratio at which the greater value correlates with the smaller one the same way as their total correlates with the greater value. Ф – irrational algebraic number whose irrationality measure equals 2. In these calculations its approximated value Ф=1.618034 is used. This ratio is widely present in nature, engineering, science, art, biology and medicine. For instance, in physics for some oscillatory systems their technical characteristics are proportional to “golden ratio”.

It can be assumed that when constructing pyramids Egyptians knew not only about “golden section” and π, but they also had the idea of geodesic angle. But in the pyramid the geodesic angle can be the one between the pyramid edge acting as the “winding” vector and the base line which is parallel to the earth axis and goes between the northern and southern edges. Obviously, this was the reason for the pyramids to be constructed with the strict direction of edges to the cardinal points and even the location of stars in certain seasons was taken into account.

Such inclination angle of the edges in the lower part of the curved pyramid is 54°34ˈ, i.e. it differs only by 10ˈ from the geodesic angle. Such coincidence cannot be accidental, therefore, these two multidimensional parameters: golden ratio and geodesic angle must have the mathematical bond. By analogy with (6) we have:

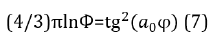
With relative error δ=0.13%.

Together with equation (6) we have:

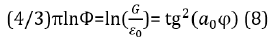
Equations (7,8) give the functional dependence of golden ratio and geodesic angle not only between each other but also with other fundamentals values. Therefore, these equations reflect the multidimensional manifestations and applications of these parameters. The value 4/3 formally corresponds to the ratio of the legs of a classical triangle. But there is a more complete explanation based on two principles of adding energy characteristics of subsystems (par. 1,2 of the initial provisions). When adding two like and similar energy parameters, their total value in the corpuscular interaction increases twice, but in the wave one – decreases twice, and their ratio equals 4. In this spatial direction one part of this value equals 4/3. Such number can be also found in other equations, for instance:

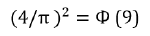
where δ=0.09%.

In this equation 4/π characterizes the angular distribution of corpuscular-wave ratios.

Did the Egyptians also plan to construct other pyramids with the geodesic inclination angle?

Thousands of years have passed since the construction of the pyramids and now it is impossible to precisely determine the initial dimensions and inclination angle. Many pyramids were considerably destroyed and partly deconstructed. Therefore, at present, the inclination angle of the edges is not the geodesic angle (for the majority of the pyramids). In this investigation it is designated as α – inclination angle of the edges of the pyramids at present.

But in the technical characteristics of the pyramids the mathematical bond between angles  and α and “golden ratio” should be preserved, though approximately. Table 1 contains the most famous pyramids with the right pyramidal shapes and inclination angles of 51°-52° (for three pyramids) and inclination angle of 43°21´ (for two pyramids). It is also taken into account that Chephren Pyramid has the edges with different inclination angles.

The calculations demonstrated (Table 1) that the functional bond is available:

Table 1:

A. For pyramids with the edge inclination angles of 51°-52°:

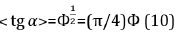
˃= =(π/4)Ф (10)

where ˃ – average value for three pyramids equaled to 1.2679.

Since the value (π/4)Ф=1,2708, we have δ=0.22%.

B. For pyramids with the inclination angle of 43°21´:

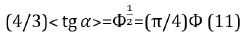
(4/3) ˃= =(π/4)Ф (11)

where δ=0.96%.

The value (π/4)Ф indicates that the actual values of  obtained by the edge inclination angle, at present, correspond to the rule of “golden ratio”. Mycerinus Pyramid has the greatest deviation from this rule. But only in the Middle Ages this pyramid was two times considerably destroyed and affected.

1. The geometric-geodesic angle is the angle between the rotation axis and rotation vector. In a stationary system it can be physically found through the triangle angle tangent, in which its legs are the components of corpuscular-wave process.
2. The equation of such functional dependencies was obtained in kinetics of structural interactions of some macro- and microsystems (for gravitation, as well). 3. The equations of metamathematical bond between “golden ratio” and geodesic angle, as well as with other fundamental values are given.
3. As applicable to technical characteristics of Egyptian pyramids, it is demonstrated how their proportions correspond to the rule of “golden ratio”.

1. SP Finnikov (1961) Differential geometry. М.: MSU Publishers.
2. https://ru.wikipedia.org/wiki/Геодезическая
3. Yu M Pidgainy, VM Morozova, VA Dudko (1967) Mechanics of polymers, pp. 1096-1104.
4. T Yu (2005) Ayusheev. Geometric issues of adaptive technology of structure production by winding from fibrous composite materials. – Ulan Ude: Buryat Research Center Publishers.
5. V.I. Kodolov. Polymeric compositions and technology of aircraft engines production from them. Izhevsk Mechanical Institute, p. 200.
6. GА Korablev (2006) ON PROBLEMATIC ISSUES OF PHYSICAL CHEMISTRY, JMEST 6: 10320-10324
7. RG Gevorkyan, VV Shepel (1972) Course of general physics. Vysshaya shkola, p. 600.
8. GА Korablev (2019) On the mechanism of gravitation processes, JMEST 12: 705-714.
9. https://ru.wikipedia.org/wiki/Традиционная_китайская_медицина
10. https://ru.wikipedia.org/wiki/Египетские_пирамиды