On the Moving Distributed Force Problem of a Non-Uniform Prestressed Simply Supported Rayleigh Beam

Prestress is the application of an initial compressive load on the structure. Its building advantages include allowing reducing crack incidence and element dimensions by the use of more resistant materials. It promotes a long service life of the element of the structures and therefore the structures may need low or no maintenance. Under constant compressive or tensile force, [1,2] computed natural frequencies of Bernoulli-Euler beams. In the latter, under tensile loads and in the former, under compressive axial loads. Later, [3] investigated the forced vibration of an elastic uniform Bernoulli-Euler beam having simple supports with a constant axial force resting on variable elastic foundation and traversed by uniformly distributed loads. [4] studied the transverse vibration of a Rayleigh cantilever beam with arbitrarily distributed axial loading and carrying a concentrated mass at the free end. Recently, [5] investigated the vibrations under distributed loads moving with constant velocities of a non-prismatic prestressed Rayleigh beam on an elastic foundation. Analytical solutions to the governing equation were obtained for the simply supported and clamped ends boundary conditions. Conditions under which resonance occur were established.

The moving distributed force problem is an approximate model which assumes the inertia effect of the moving distributed mass as negligible.

Simply supported boundary conditions

In this case, the displacement and bending moment of the non-uniform prestressed beam both vanish.

Thus, the moving distributed force problem reduces to a non-homogeneous second order ordinary differential equation,

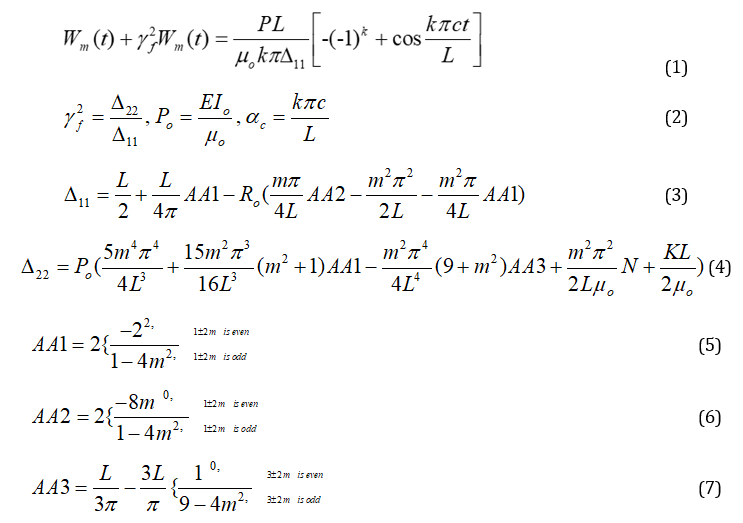
is the mass of the beam

is the moment of inertia

𝐿 is the Length of the beam

𝑥 is the spatial coordinate

𝑡 is the time variable

𝐸 is the Young’s modulus

is the measure of rotatory inertia effect

𝑁 is the prestress constant and

𝐾 is the elastic foundation constant.

Solving equation (1) by means of Laplace transforms and Convolution theory with the initial conditions written as,

one obtains an expression for 𝑊𝑚(𝑡) which on inversion yields

Equation (9) represents the transverse displacement response to a distributed force moving with constant speed of a simply supported non-uniform prestressed Rayleigh beam resting on an elastic foundation.

At this point, it is important to establish conditions under which resonance occurs. Resonance takes place when the motion of the vibrating structure becomes unbounded. That is, when the vibrations become intensive. In actual practice, when this happens, the structure would probably break as the intensive vibrations cause cracks, permanent deformation and destruction in the frequently vibrating structures. Equation (9) clearly shows that the beam reaches a state of resonance when,

1. Bokaian A (1988) Natural frequencies of beams under compressive axial loads. Journal Sound Vibration 126(1): 49-65.
2. Bokaian A (1990) Natural frequencies of beams under tensile axial loads. Journal Sound and Vibration 142(8): 481-498.
3. Omolofe B, Ogunyebi SN (2009) Transverse vibrations of elastic thin beam resting on variable elastic foundation and subjected to travelling distributed forces. The Pacific Journal of Science and Technology 10(2): 112-119.
4. Li XF, Tang AY, Xi LY (2013) Vibration of a Rayleigh cantilever beam with axial force and tip mass. Journal of Constructional Steel Research 80: 15-22.
5. Andi EA (2017) Vibrations under moving distributed loads of a non-prismatic prestressed Rayleigh beam. International Journal Dynamical Systems and Differential Equations 7(4): 328-352.