Analysis the Role of Oxygen, Light Intensity, Threshold Dose and Efficacy Improvement of Anti-Cancer via Type-II Photodynamic Therapy

Photodynamic therapy (PDT) is an effective method for anticancer via oxygen-mediated type-II mechanism, where the cytotoxic effect of PDT to tumor tissue is resulted by the generation of singlet oxygen. Efficacy of PDT is mainly influenced by: the concentration of PS drug accumulated into the cells, molecular oxygen in tissue, the light dose, intensity and dose (fluence) [1]. High concentrations of singlet oxygen can lead to necrotic cell death. In contrast, low concentrations lead to cell survival and increase the metabolism; whereas medium singlet oxygen concentrations lead to initiation of apoptosis or autophagy [2]. Therefore, the threshold light dose and singlet oxygen dose play the important role in PDT for anticancer. Recently, the singlet oxygen threshold dose, and the dosedependence cell viability curves of human cancer cells of K562 and Hela after red-light irradiation of Radachlorin were reported in vivo [3].

The kinetics and macroscopic modeling of PDT have been reported for anti-cancer using an oxygen-mediated type-II PDT [4-8] and more recently, for corneal diseases using non-oxygenmediated type-I PDT [9,10] since, the earlier work of Foster et al. [4] in 1991. Most of the previous modeling [4-8] have ignored the dynamic of light intensity and the depth-dependent profile PS and light intensity, where the exact modeling requires numerical simulations, especially when both type-I and type-II coexist [10- 12].

This study will theorize the role of concentration of PS and oxygen, rate constant, oxygen external source term, light dose, intensity and exposure time in the efficacy and threshold dose of anti-cancer via oxygen-mediated type-II mechanism. We will also analyze the measured in vitro singlet oxygen threshold dose reported by Klimenko et al. [3]. Both analytic formulas (for the first time) and numerical calculations will be presented.

Kinetcis and modeling

The kinetics of PDT for corneal collagen crosslinking was previously reported by Lin et al. [13] using UVA (365nm) initiated riboflavin solution as the photosensitizer. The three pathways kinetics are revised for a more general polymer system and briefly summarized as follows [12]. In type-I pathway, the excited PS triplestate (T3) can interact directly with the substrate (A); or with the ground state oxygen (O2) to generate a superoxide anion (O-), which further reacts with oxygen to produce reactive oxygen species (ROS). In comparison, in type-II pathway, T3 interacts with (O2) to form a reactive singlet oxygen (O*). In general, both type-I and type-II reactions can occur simultaneously, and the ratio between these processes depends on the types and the concentrations of PS, substrate and oxygen, the kinetic rates involved in the process [10].

A set of macroscopic kinetic (quasi steady-state) equation for the concentration of PS ground-state, C(z,t), and the ground state oxygen molecule [O2] was constructed [7,8,10].

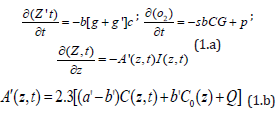
where b=aqI (z,t); a=83.6wa’; w is the light wavelength; a’ and b’ are the molar extinction coefficient of the initiator and the photolysis product, respectively; Q is the absorption coefficient of the monomer and the polymer repeat unit.

Eq. (1.a) includes the type-I term,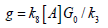, 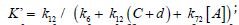and type-II; d is a low concentration correction related to the diffusion of singlet oxygen [4,7]. [A] is the substrate concentration. q is the triplet state [T] quantum yield given by 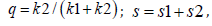with s₁ and s₂ are the fraction of [O2] converted to the singlet oxygen and other ROS, respectively, in type-I and type-II [7].

In Eq. (1.c) we have included the light intensity in the polymer given by a time-dependent Beer-Lambert law [13]. Eq. (1.b) includes the oxygen source term P( z,t) = p( 1− [O2] / [0_O]) , with a rate constant p to count for the situation when there is an external continuing supply, or nature replenishment (at a rate of p), besides the initial oxygen, [0_O], in the cells [7].

We note that Eq. (1) was also presented by Gkigkitzis et al. [6], Zhu et al. [7,8] and Klimenko et al. [3] for the anti-cancer kinetics. However, they have assumed a constant light intensity, i.e., A’(z,t) is a constant in Eq. (1.d). They also ignored the contribution from the type-I term, k₈[A], since type-II is dominant in their anti-cancer process. The previous model [6-10] have also ignored the dynamic of light intensity given by Eq. (1.c) and the depth-dependent profile PS and light intensity. Exact solutions of Eq. (1) require numerical simulations, specially when both type-I and type-II coexist [10- 12]. For comprehensive analysis and empirical formulas, we will present analytic methods and focus on type-II efficacy.

Efficacy profiles

The normalized photo-polymerization efficacy defined by Ceff =1− [A] / [A]_O = 1− exp −S , with S-function, for a type-II dominant process, given by [10].

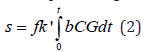
where f = k₇₂[ A] / k₁₂ , proportional to the substrate concentration [A]. We note that the S function is proportional to the cumulative singlet oxygen generation, [¹O₂], multiplied by a factor f, and [¹O₂] =bK’CG.

Analytic formulas

For analytic formulas, three methods are available for the effective extinction coefficient: (I) using the mean light intensity given by I’(z) = 0.5(I1+ I 2) , with Ij = I₀exp (−Ajz) ; A1 = 2.3aC₀ +Q , and 2 0 A = 2.3bC +Q; (ii) a mean (over z) C’(t), A(t) = 2.3(a − b)C’(t) +Q , in which C’(t)is a decreasing function of time, such that l (z,t) is an increasing function of time; and (iii) using a time-dependent light intensity given by 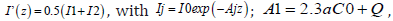where t* is the crosslink steady-state time (t*) defined by when the PS concentration is depleted to 0.018 (or 1/e4) of its initial value, given by t* = 4m’ / [a’I ( z, t )] , which is inverse proportional to the light intensity. we will use an effective A(z,t) or its mean value, such that A’(z,t) becomes time-independent in solving Eq. (1). The effective extinction coefficient is given by [12], A = 2.3a’m (1− 0.25z / D) C₀ +Q . with m is a numerical fit parameter, m=0.4 to 0.6 depending on the value of a’ and b’.

In Eq. (1.a), for type-I dominant case (with g’<< g), C(z,t) has a simple exponential decaying function of bK’, if b (or light intensity) is not time-dependent, given by 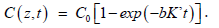However, for general case with time-dependent light intensity, C(z,t) has a more complex decaying function and requires a numerical solution. For the case of simple exponential decaying, the value of bK’ = (aqgK’) I (z,t ) , may be empirically found if C(z,t) is measured.

Type-II process is much more complex than type-I due to the complex function of G(z,t) which depends on oxygen concentration and requires numerical solutions [12,13]. For analytic formula in type-II dominant case (with g’>>g), and for the low concentration correction, d>>C₀, we assume an approximated PS concentration given by a similar form as type-I, C (z,t) = C₀ Fexp −Bt , with B = dbK’,b = aqI (z) ; the oxygen concentration, [O2], may be obtained by solution of Eq. (1.b) which leads to the solution of a nonlinear equation as follows:

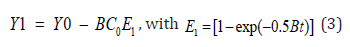
and Y1 = [O2] + kln[O2], Y0 = [O₀] + kln[O₀.] . Eq. (4) still needs numerical solution for the oxygen concentration, [O2], and will be shown later. Approximate solution is given by [O2] = [O₀] – mt, m = f ’bC , with f’ is a fit parameter. Therefore, G=N –N’ t, with 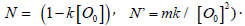. The secondorder PS concentration then becomes , with B₁ t = bK (N − 0.5N’t) , which reaches its steady-state (C’), when oxygen is completely depleted, or [O2]=0 at t=t’, and the steady-state given by

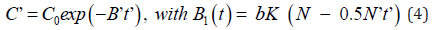
We note that higher C₀ leads to faster depletion of oxygen, as shown by Eq. (4), and has a smaller t’, which also gives smaller value of B’t’ leading to a larger C’. This feature will be justified by our numerical results later. Moreover, C(t) is decreasing function less strong than a simple exponential rate of bKNt due to the negative term of -0.5N’t².

Using he analytic functional forms for C(t), the time integral of Eq. (2) gives us, for k<< [O0] and P=0,

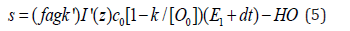
with I’=0.5(I₁+I₂) is a mean light intensity, and HO is a highorder term.

Eq. (5) shows that the type-II efficacy is an increasing function of I₀C₀ [O0]; It has a transient state (with E1=t) proportional to the light dose, I₀t; and steady-state is only dose-dependent (for the case of P=0), to be justified by numerically later.

Dynamic profiles

The following numerical results are for type-II (with g<< g’) and light intensity given by 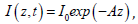, with A=0.3C(z,t); and the parameters of [5]: k=8.7um, d=33um, [O0]=220um, b = b’I (z,t ) ; p, K’, b’, I₀, and C₀ will be adjustable variables to explore their roles in the efficacy and cell viability. Moreover, the light intensity is simplified to a constant,I (z,t) = I₀ , which is valid for thin cell layer, such that exp(-Az) =1. The more general case with time-dependent I(z,t), for z>0 (or thick cell system) will be presented elsewhere.

Eq. (1.a) shows that when oxygen is depleted, with [O2]=0, G=0, and C(z,t) reaches its steady state constant value (for the type-II dominant case), bK’/B. This implies that C(z,t) and [O2] have the same decaying rate to reach their steady states, which also define the maximum efficacy, or minimum cell viability. We will present the role of these parameters: C₀, [O0], p, K’, I₀, light dose, or exposure time as follows. Referring to Figure 1 to 4 for the time profiles of oxygen, PS concentration, S-function and cell viability (CV), the following important features are summarized.

Figure 1:Normalized PS concentration, C(t), vs. time for various initial PS concentration, C0= (5,10,15)uM (for curve 1,2,3) and fixed value of [O]0=100uM, K’=0.0025 (1/um), and p=0, for light intensity I0= 20 and 50 mW/cm2, for Figure (A) and (B), respectively.

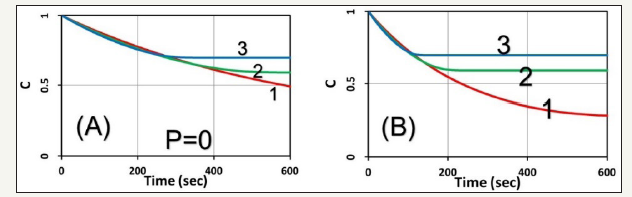
Figure 2:Normalized oxygen concentration, y=[O2], vs. time associate to Figure 1.

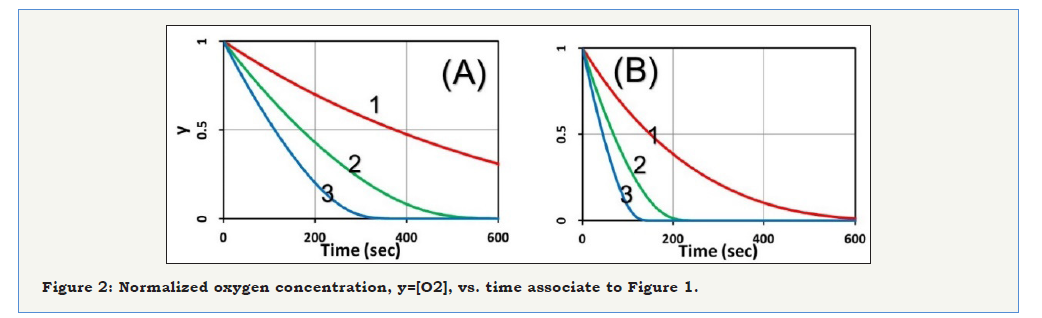
Figure 3:Cell viability (CV) vs. time associate to Figure 1 (for p=0).

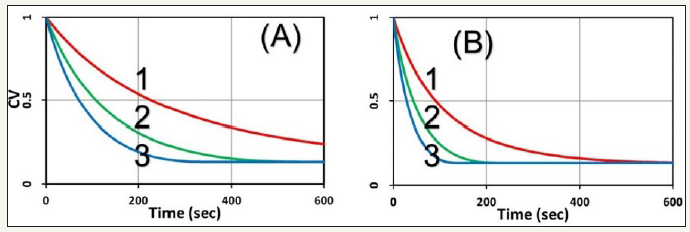
Figure 4:Same as Figure 1 for the normalized PS concentration vs. time but for p=0.2 (uM/s), for light intensity I0= 20 and 50 mW/cm2, for Figure (A) and (B), respectively.

The role of C₀ and I₀: The role of initial PS concentration (C₀) and light intensity (I₀), are shown by (Figure 1), the normalized PS concentration vs. time for the case of no external oxygen supply (or p=0) for various initial PS concentration, C₀= (5,10,15)uM, and fixed value of [O₀] =100 uM , K’ = 0.0025 (1/ uM ) , aq = 0.02(cm² / mW / s) , with intensity I = (20, 50) mW / cm² . The oxygen concentration profiles are shown in (Figure 2); and cell viability, defined by CV=1- exp(-S) is shown in (Figure 3). Higher C₀ and/or light intensity (I₀) result a faster PS and oxygen depletion leading to a higher efficacy, or lower CV. As shown by (Figure 3), CV reaches approximately 0.2 at 400 seconds, fo I = 20 mW / cm² , comparing to 200 seconds for I = 20 mW / cm² , and both have the same dose of 4 J/cm². Therefore, the CV is mainly determined by the light dose and follow the socalled Bunsen Roscoe law (BRL) for the case of p=0 in the type-II process. This BRL is slightly revised when p>0, in contrast to type-I efficacy which follows a non-BRL.

As shown by (Figure 2), without the external oxygen supply (with p=0), oxygen is depleted by a negative slope proportional to bC₀, referring to Eq. (5). Therefore, higher C₀ and/or light intensity (I₀) has a faster depletion rate. As shown by (Figure 1), C(t) reaches a steady-state (C’) when oxygen is completed depleted; noting that C’ is higher for higher C₀, as also shown by our analytic Eq. (4), for a smaller t’ (or faster oxygen depletion). Moreover, C(t) is a decreasing function less strong than a simple exponential rate of bKNt due to the negative term of -0.5N’t², as predicted by Eq. (4).

Profiles for p>0: With the external oxygen supply (with p>0), above feature changed significantly, comparing to (Figure 1), that the PS concentration shown by (Figure 4) does not reach a steadystate, but continuously decreases due to the replenishing oxygen, as shown by (Figure 4), (Figure 5) shows the oxygen profiles, in which higher C₀ and/or light intensity (I₀) results to faster oxygen and PS depletion, and leading to lower CV, as shown by (Figure 5).

Figure 5:Normalized oxygen concentration vs. time associate to Figure 4 (for p=0.2 uM/s).

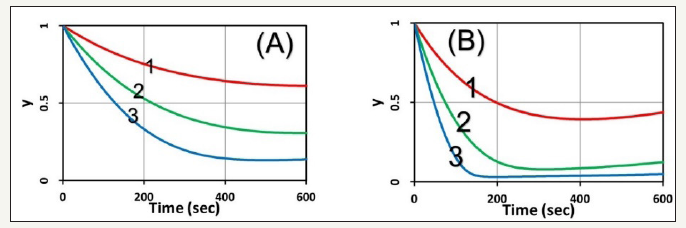
Figure 6:Cell viability for p=0 and p=0.4 (uM/s) shown by (A) and (B), respective; also shown are the threshold time (t*) to reach a cell viability CV*< 25%.

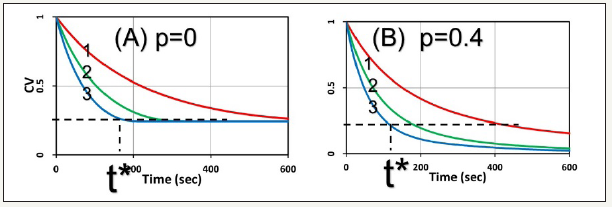
The threshold dose: Figure 6 show the cell viability for p=0 and p=0.4 (uM/s), respective. They show that the cell viability, defined by CV=exp(-S), is lower for higher C₀ and/or light intensity (I₀). Moreover, with p>o, external oxygen offers lower CV, or better cell killing. It also shows the threshold dose E*=I₀t* (or time t* for a fixed light intensity) to reach a cell viability CV*<25%, is higher for smaller C₀ and/or I₀, in consistent with the measured data of Klimenko et al. [5], in which CV also follows out formula of CV=exp(-S), referring to their (Figure 5). Moreover, (Figure 6) also shows that the product of C₀E* follows BRL for the case of p=0, whereas BRL is invalid for the case of p>0 (with external oxygen supply).

Efficacy improvement

Clinically, the external oxygen supply may be from the blood circulation in the cancer cells. For the situation for such as skin or oral cancer in which extra PS may be applied to the cancer tissue surface to improve its efficacy. As shown by S-formulas, Eq. (5), for the anti-cancer type-II PDT efficacy S~ [O2]C, which requires both PS concentration C and [O2]. Therefore, resupply of PS or oxygen would enhance the generation of singlet oxygen radicals and improve the anti-cancer efficacy via type-II PDT. This new strategy has been proposed in type-I corneal crosslinking [13], but not yet in anti-cancer PDT. Therefore, further experimental/clinical studies are highly desired.

We have demonstrated that our formulas predict very well the measured results of Klimenko et al. [3]. However, the accuracy of our formulas will require accurate measurement of the parameters involved, such as the rate constant (K), the quantum yield (q), the molar extinction coefficient of the initiator (a’) and the photolysis product etc. In addition, further experimental measurements should also include the roles of PS concentration and light intensity. Our group has been working on the in vitro measurement of cell viability, which may be empirically analyzed by our formulas. Further study will be published elsewhere.

For the same dose, lower light intensity achieves a higher steady-state-efficacy (SSE) in type-I; in contrast to type-II, in which the efficacy is mainly dose-dependent. Type-II process is also affected by the available oxygen. Without external oxygen supply, higher light intensity produces more efficient singlet oxygen, resulting a higher transient efficacy, in which all intensities reach the same SSE when oxygen is completely depleted. With external oxygen, type-II efficacy increases with time and dose without a steady-state limitation. The overall efficacy may be enhanced by resupply of PS or oxygen during the light exposure.

This work was supported by the internal grant of New Vision Inc. KT Chen is partially supported by the Ph.D program of Graduate Institute of Applied Science and Engineering, Fu Jen Catholic University, Taiwan.

1. Lin JT (2018) Advances of cancer synergic photo-therapy: kinetics and efficacy. Nov Appro in Can Study 2(1): 1-5
2. Straten DV, Mashayekhi V, de Bruijn HS, Oliveira S, Robinson DJ (2017) Oncologic photodynamic therapy: basic principles, current clinical status and future directions. Cancers 9(2): 19.
3. Klimenko VV, Shmakov SV, Kaydanov NE, Knyazev NA, Kazakov NV, et al. (2017) In vitro singlet oxygen threshold dose at PDT with Radachlorin photosensitizer. Proc SPIE:10047.
4. Foster TH, Murant HRS, Bryant RG, Knox RS, Gibson SL, et al. (1991) Oxygen consumption and diffusion effects in photodynamic therapy. Radiat Res 126(3): 296-303.
5. Finlay JC, Conover DL, Hull EL, Foster TH (2001) Porphyrin bleaching and PDT-induced spectral changes are irradiance dependent in ALAsensitized normal rat skin in vivo. Photochem Photobiol 73(1): 54-63.
6. Gkigkitzis I, Feng Y, Yang C, Lu JQ, Hu XH, et al. (2012) Modeling of oxygen transport and cell killing in type-II photodynamic therapy. Photochemistry and Photobiology 88(4): 969-977.
7. Zhu TC, Finlay JC, Zhou X, Li J (2007) Macroscopic modeling of the singlet oxygen production during PDT Proc SPIE 6427: 6427O81-6427O812.
8. Kim MM, Ghogare AA, Greer A, Zhu TC (2017). On the in vivo photochemical rate parameters for PDT reactive oxygen species modeling. Phys Med Biol 62(5): R1-R48.
9. JT Lin, DC Cheng (2017) Modeling the efficacy profiles of UV-light activated corneal collagen crosslinking. PloS One 12(4): e0175002.
10. Lin JT (2018) Efficacy S-formula and kinetics of oxygen-mediated (type-II) and non-oxygen-mediated (type-I) corneal cross-linking. Ophthalmology Research 8(1): 1-11.
11. Lin JT, Chen KT, Liu HW (2018) Analysis of kinetics and efficacy of anticancer via oxygen-enhanced photodynamic therapy. J Cancer Research update 7(1): 21-23.
12. Lin JT (2018) Optimal efficacy in light-activated biomedical systems and nonlinear laws versus linear Beer-Lambert law and Bunsen-Roscoe reciprocal law. Op Acc J Bio Eng & Biosc 1(5): 1-4.
13. Lin JT (2018) A proposed concentration-controlled new protocol for optimal corneal crosslinking efficacy in the anterior stroma. Invest Ophthalmol Vis Sci 59(1): 431-432.