Neuroblastoma and Glioblastoma Brain Cancers: «Human Genome Optimum» (HGO) a Global Genome Strategy controlling all Human Chromosome LOH Deletions

Background

Thanks to the CRISPR (Clustered regularly interspaced short palindromic repeats) technology, it is now possible to locally modify the genomes, and particularly the human genome [1]. Almost simultaneously, the fractal and global structures of the human genome were demonstrated [2]. In such a context, apart from ethical questions, can a local technology as powerful as CRISPR be applied, ignoring its possible effect on the possible global and long-range equilibria and balancing at the chromosome scale or even the entire genome scale? For more than 25 years, we have been looking for possible global, even numerical, structures that would organize DNA, genes, chromosomes and even whole genomes [3-6]. Curiously, the method of numerical analysis of whole genomes as well as the discovery of a global law of impact of the LOH deletions associated with tumors that will be the subject of | this article may seem to the reader too simple or even “naive”... In effect, these laws are based on a well-known type of analysis that could be thought to have explored all aspects: the analysis of GC/TA ratios. It has long been known that such ratios [7] characterize the diversity of chromosomes. Under the name of “isochores,” Giorgio Bernardi has extensively explored its richness and diversity [8,9]. We have already demonstrated a numerical structure at the scale of each human chromosome as well as on the whole genome [10- 13]. In [10] we have already highlighted this numerical value of 0.6909830056, the HGO in this article: it controls the population of triplet’s codons analysing single stranded DNA sequence from the whole human genome. However, it is only by deepening the notion of “fractal periodicity”, outlined in [14], and we will highlight in various articles in preparation [15] that we have re-discovered the major role that this GC/TA ratio at the whole chromosome and whole genome scales. Particularly, in 2015, we have demonstrated [14] how a global structure organizes any DNA sequence. This numerical organization is based on the atomic masses of the “G” bases of the double stranded DNA sequence, therefore on the bases C and G of the single stranded DNA sequence. Here is another reason sufficient to consider the relations and proportions between bases C + G on the one hand, and T + A on the other hand. Comparing the three genomes of reference of Neanderthal [16], Sapiens Build34 of 2003 [17] and Sapiens hg38 of 2013 [18], we will demonstrate in [15] the evidence of “Fractals periods”and “resonance periods” characterizing each of the 24 human chromosomes. It is for these simple reasons that we have decided to focus on these C + G/T + A ratios at the scale of each of the 24 human chromosomes as well as on the whole genome analysing the 46 chromosomes single stranded DNA sequences.

Material and Methods

Analysed whole human genomes

We analyzed completely and systematically each of the 24 chromosomes of each of the following three reference genomes:

Neanderthal genome

a. Neanderthal genome [16]

b. Sapiens Build34 [17]

c. Sapiens Build34 (2003) genome

d. Sapiens hg38 human reference genome [18]

e. Sapiens hg38 (2013) genome

Computing the HGOs

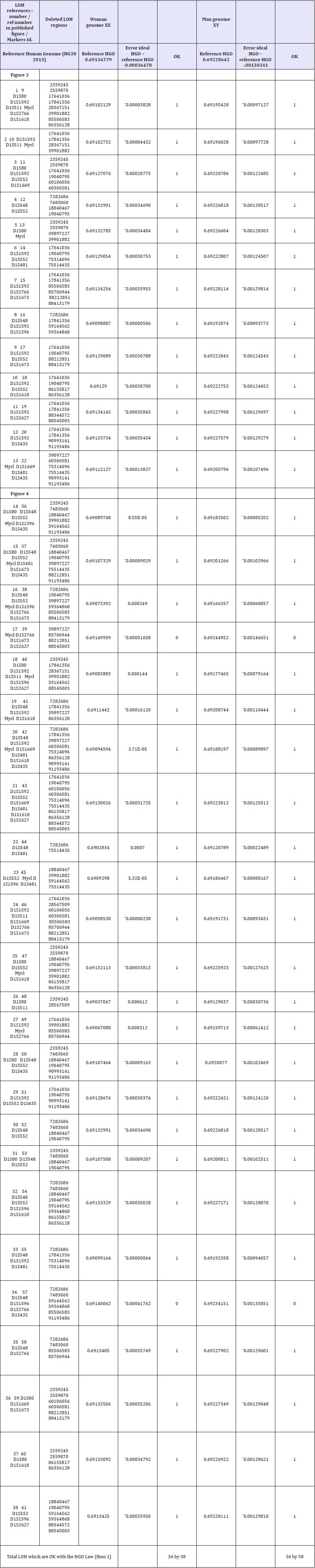
LOH selection criteria: We retain only the LOH corresponding to regions delimited by 2 markers, as well as regions comprising at least 2 markers alone. The analyzed LOH deletions may vary from a single deletion of a single region to 2, 3, 4, 5 or 6 non-contiguous regions deleted in the same chromosome. Indeed some LOH are reduced to a single marker, that is to say approximately 200000bp, which is too insignificant. Selection LOH region example, the first of the markers delimited LOH region in this study is D10S249 D10S211: chr10: 134851 - 21719222.

Let us now distinguish the three types of HGO that will be discussed

a. Theoretical HGO (tHGO)

tHGO = (3-Phi)÷2 = 0.6909830056, where Phi is the Golden Ratio Phi = 1.618033989

b. Reference female HGO (rwHGO) : rwHGO = 0.6913477936 error (tHGO – rwHGO) = 0.6909830056 - 0.6913477936 = ¯0.0003647879784 and

c. Reference male HGO (rmHGO) : rmHGO = 0.6922864236 error (tHGO – rmHGO) = 0.6909830056 - 0.6922864236 = ¯0.001303417973

Computing HGO (LOH) function and errors: HGO (LOH) is considered as a function: with LOH the deletion disturbing the computed CG/TA whole human genomic ratio and « n » the LOH partially deleted chromosome and « chrs » all chromosomes from 1 to 22 which are different with « n ». HGO is computed by compiling C+G and T+A nucleotides populations from each 46 chromosomes DNA single strand.

Example:

HGOwoman (LOH chr n) = (C+G population from 46 chromosomes strand1) + (C+G population from 46 chromosomes strand1)] [ (T+A population from 46 chromosomes strand1) + (T+A population from 46 chromosomes strand1) ] Then: HGOwoman (LOH chr n) = [ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrX) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrX) ]

HGOman (LOH chr n) = [ (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chrn) + (sum C+G chrX) + (sum C+G single strand 1 to 22 chromosomes except chrn) + (sum C+G chr LOH n) + (sum C+G chrY) ] [ (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chrn) + (sum T+A chrX) (sum T+A single strand 1 to 22 chromosomes except chrn) + (sum T+A chr LOH n) + (sum T+A chrY) ]

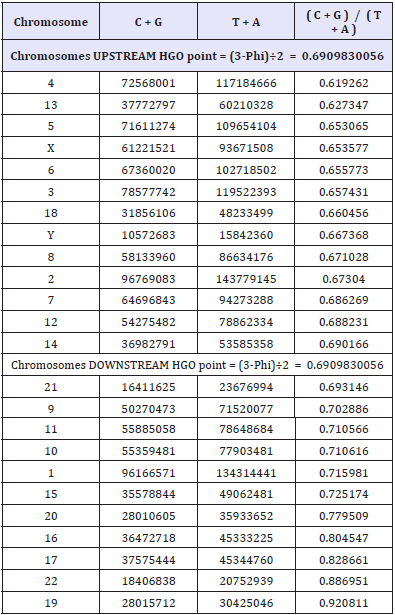
Recall the single stranded C+G, T+A and individual chromosome HGO values (Table 1).

Table 1: CG values, TA values and CG/TA ratio for each Sapiens HG38 individual chromosome.

Results

In all that follows, the general methodology will be as follows: we calculate, for the 46 chromosomes constituting each genome studied, only the single-stranded DNA sequences. In these sequences, we count the relative populations of bases T + A on the one hand, and C + G on the other hand.

HGO of the 3 Whole Genomes : Neanderthal, Sapiens Build 34 and Sapiens HG38

The three genomes we compare here are differentiated on the one hand by their respective evolution levels, on the other hand by the sample of individual genomes of which they form the syntheses, and finally by the precision of the sequencing of DNA.

For example, this work by the Craig Venter team demonstrates this level of dispersion between more than 10,000 individual genomes and reference genomes such as HG28 [19].

The 3 analyzed genomes are:

d. Neanderthal genome [16]

e. Sapiens Build34 genome [17]

f. Sapiens hg38 genome [18]

The detailed data related to the 3 whole genomes shows the various distances and errors between real computed HGOs for each genome and theoretical HGO optimum value = 0.6909830055.

The detailed data related to the 3 whole genomes shows the various distances and errors between real computed HGOs for each genome and theoretical HGO optimum value = 0.6909830055.

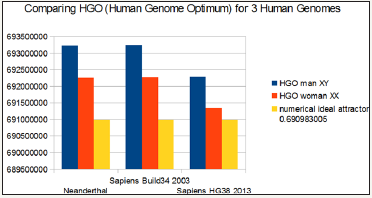
It is also observed that female genomes (XX) are more optimal than male genomes (XY).

On the other hand, the genomes of Neanderthal and Sapiens (Build34 of 2003) have very close optimization levels. We believe this result from the fact that the precisions of their respective DNA sequencing are similar.

On the contrary, the hg38 genomes of 2013 show the most optimal levels, this is most certainly due to the deeper quality of their DNA sequencing. Figure 1 summarizes HGO results for these 3 human genomes of varying levels of evolution.

Figure 1: The respective HGOs of 3 human genomes of varying levels of evolution are shown here.

HGO Spectral Hierarchy of the 24 Human Chromosomes

The following 2 figures (Figure 2 & 3) illustrate the hierarchical spectrum of the individual HGOs of each of the 24 chromosomes for each of the three genomes analyzed. It should be noted that the upstream / downstream tipping point lies between chromosomes 14 and 21, which is closely related to the probable mechanisms explaining trisomy21 (whose disorders involve precisely these two chromosomes).

Figure 2: HGO diversity of human chromosomes UPSTREAM of the numerical attractor HGO = 0.6909830056.

Figure 3: Diversity of HGOs of human chromosomes DOWNSTREAM of the numerical attractor HGO = 0.6909830056.

Finally, we note that it is the downstream region (Figure 3) that contributes the most to the superiority of optimality of sapiens hg38 compared to sapiens Build34. However, a more detailed analysis of the upstream and downstream regions shows that when passing from sapiens Build34 2003 to hg38 2013, the notorious optimization obeys the global strategy law of the LOH. Also of note is that 20 out of 24 chromosomes are OK, with the exception of chromosomes 13, X, Y, and 1. The law presented here states that there is reduction of optimality for upstream chromosomes and improvement of optimality for downstream regions.

It is therefore remarkable that this is the same and only law which seems to simultaneously control two domains as different as: 1) the global strategy of LOH deletions of tumors on the one hand and 2) the difference of evolution of the same genome following two increasing precision levels of DNA sequencing (Build34 2003 and hg38 2013) on the other!

We have sorted the 24 chromosomes by increasing values of CG/TA ratios in the 3 cases of compared genomes (Figure 1).

It then reveals a hierarchical classification scale of 24 chromosomes ranging from 1 / Phi (chromosome4) to 3/2 Phi (chromosome 19).

HGO Disturbed by 240 LOH Deletions Related to 5 Different Chromosomes and 5 Different Tumors

After demonstrating how 3 human genomes with increasing levels of sequencing quality and evolution accuracy seem to “fit” this theoretical value of HGO, we will now analyze how small mutations on one of the chromosomes can “disrupt” this HGO. For this purpose there are a very large number of publications associating such nucleotide regions with deletions of the chromosomal DNA of different tumor cells.

We analyzed the Loss of Heterozygosis’ associated with 240 cases published in [20-25]. These 240 cases relate successively to the Breast [20,21], Glioblastoma [22], Colorectal [23], Neuroblastoma [24], and Prostate [25] cancers. They successively affect the chromosomes 13, 5, 10, 1 and 16.

This exhaustive analysis will then reveal the following generic law

“When an LOH deletion affects a chromosome upstream of the HGO point (Figure 1, chromosomes 4 13...) in the chromosomal spectrum, this deletion degrades the genomic optimum of the cancer genome.

When an LOH deletion affects a chromosome downstream of the HGO point (Figure 1, chromosomes 19 22...) In the chromosomal spectrum, this deletion improves the genomic optimum of the cancer genome. (Table 2)

Global graphical analysis of the 240 LOH tumor cases

In Figures 4-6 &7 below present an overall analysis of the HGOs resulting from the 240 cases of LOH deletions associated with 5 types of cancers and 5 distinct chromosomes.

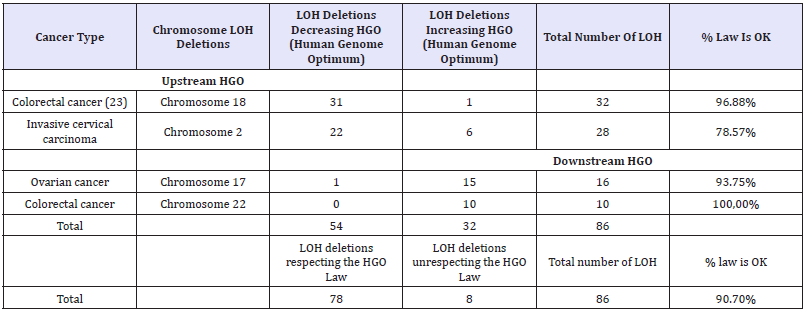
Table 2: Table of synthesis of 240 LOH relating to 5 types of cancer and 5 different chromosomes. The shaded areas represent those that comply with the HGO law, ie 227 cases out of 240. In blue the 53 caeses related to Neuroblastoma and Glioblastoma cancers.

In the Table 2 the shaded areas represent cases of LOH complying with the generic rule, while the unshaded areas represent cases of LOH that do not comply with this rule. In total, 227 cases respect the rule and only 13 cases of LOH do not respect it, a success rate of this law equal to 94.58%. In particular, on 53 cases of LOH mutations analyzed for the two types of Glioblastoma and neuroblastoma cancers, the HGO optimality law is verified in 50 cases and in failure for only 3 cases, ie a percentage of validity of this universal law equal to 94.24. %.

Figure 4: Case of a woman genome, the 82 on the left are for decreased HGO chromosomes: 1/ at the bottom axis level, the theoretical HGO, 2/ in blue, the reference woman HGO value, then, 3/ the 240 LOH cases curve : on the left part of the figure LOH HGO values are principally higher than reference woman HGO, on the right part of the figure LOH HGO values are principally lower than reference woman HGO.

Figure 5: Case of a woman genome, the 82 on the left are for decreased HGO chromosomes: 1/ at the zero axis level, the theoretical HGO, 2/ in blue, the reference woman HGO error, then, 3/ the 240 LOH cases curve: on the left part of the figure LOH HGO errors are principally higher than reference woman HGO error, on the right part of the figure LOH HGO errors are principally lower than reference woman HGO error.

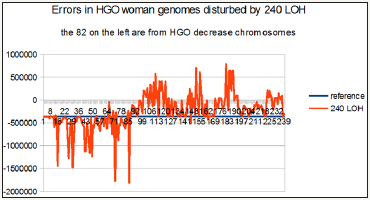
Figure 6: Case of a man genome, the 82 on the left are for decreased HGO chromosomes: 1/ at the bottom axis level, the theoretical HGO, 2/ in blue, the reference man HGO value, then, 3/ the 240 LOH cases curve : on the left part of the figure LOH HGO values are principally higher than reference man HGO, on the right part of the figure LOH HGO values are principally lower than reference man HGO.

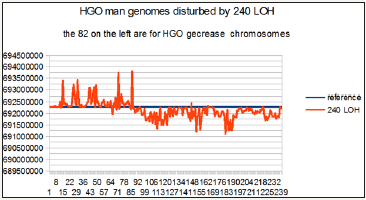
Figure 7: Case of a man genome, the 82 on the left are for decreased HGO chromosomes: 1/ at the zero axis level, the theoretical HGO, 2/ in blue, the reference man HGO error, then, 3/ the 240 LOH cases curve : on the left part of the figure LOH HGO errors are principally higher than reference man HGO error, on the right part of the figure LOH HGO errors are principally lower than reference man HGO error.

For this purpose we recall how to distinguish 3 types of HGO:

a. The theoretical HGO: (3-Phi)÷2 = 0.6909830055, where Phi is the « golden ratio » Phi = 1.618033...

b. The 2 reference HGOs relating to the respective hg38 reference genomes of the female (0.691347793) and man (0.692286423).

c. The 240 HGOs relating to each of the 240 chromosomes having ubi LOH deletions.

On the other hand, the chromosomes are presented in these 4 figures according to the order sequence of the hierarchical spectrum shown in Figure 2 & 3 above.

Consequently, these 240 cases are presented in the order of upstream towards downstream with respect to the theoretical HGO.

In particular, this is the case for the first 82 LOHs for breast tumors affecting chromosomes13 and 5, both of which are upstream (Figure 2), on the contrary, all remaining LOHs will be downstream (Figure 3) of the theoretical HGO point, thus downstream.

Thus, Figure 4 & 6 will synthesize the relative positions of all these HGOs.

Similarly, the errors or distances Figure 5 & 7 will also be calculated relative to the respective distances between HGO of the 240 cases of LOH deletions, or of the reference HGOs, with respect to the HGO theoretical.

These 4 graphs of Figure 4-7 summarize the relevance of the generic law in visual form. Indeed, the fact of having ordered the chromosomes and their associated LOHs according to the classification of the 24 chromosomes of Figure 2 has helped to highlight the statistical reality of this law.

We have successively demonstrated that, in the Human Genome Evolution and in the precision of sequencing of the genomes, these genomes seemed to “seek” a sort of numerical optimum: HGO (Figure 1).

Then, we demonstrated how the LOH deletions affecting the tumor cell chromosomes obeyed a generic law based on the chromosome hierarchization illustrated in Figure 2 & 3.

However, an important open-ended question: do these LOH deletions affecting the HGO optimum have any potential significance for the pathogenicity and aggressiveness of these tumors? This is what we are going to demonstrate now.

First analysis : 15 Glioblastoma tumors LOH in Chromosome 10

Glioblastoma is a particularly dangerous brain cancer. Glioblastoma (World Health Organization [WHO] Grade IV) is the most frequent and malignant human brain tumor, occurring at a frequency of two to three cases per 100,000 population and per year for most European and North American countries.

Basic Data

The article supporting our analysis: [22]

The chromosome support of our analysis: chr10:1- 133,797,422 133,797,422 bp.

Allelic patterns of chromosome 10 in 17 primary and 13 secondary glioblastomas. Case numbers are indicated at the top of each column. The overall frequency of loss of heterozygosity (LOH) on chromosome 10 is similar in both glioblastoma subtypes but the extent of chromosomal loss differs. Primary glioblastomas often show complete loss (10p,q) while in secondary glioblastomas, LOH is typically restricted to the long arm (10q).

Basic results (Table 3)

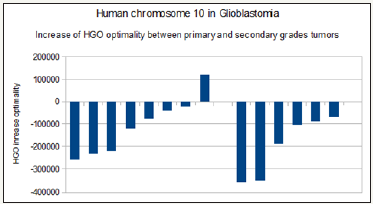
To conclude: Note that the chromosome 10 is downstream with respect to the tipping point HGO (Figure 3). Therefore, by virtue of our “global LOH strategy law by chromosomes”, the majority of LOHs “should” improve the HGO value: in effect, it is observed that 14 cases out of 15 increase the HGO.

Second analysis : 38 Neuroblastoma tumors LOH in Chromosome 1: Neuroblastoma is a very complex form of brain cancer, often involving LOH on several chromosomes. A very pathogenic form is based on LOHs of chromosome 1p. From this published paper [24], we studied and then compared respectively the evolution of the HGO for 13 LOH of local / regional tumors, then 25 other LOHs of highly pathogenic stage 4 tumors.

Table 3: Detail of 15 Glioblastoma tumors LOH deletions of chromosome 10.

Basic Data

The article supporting our analysis: [24]

The chromosome support of our analysis: chr1:1- 248,956,422 248,956,422 bp.

The 2 figures supporting our analysis:

Local-regional tumors with LOH at diagnosis. Approximate map location of polymorphic markers is shown at the left. Shading highlights the region of potential loss at 1p36, the most commonly deleted area, and defines the shortest region of overlap. Black boxes represent LOH, gray boxes are non-informative loci, white boxes are retained heterozygosity, and hatched boxes indicate microsatellite mutations.

Stage 4 tumors at diagnosis with LOH involving shortest region of overlap on 1p36. Approximate map location of polymorphic markers is shown at the left. Shading highlights the region of potential loss within 1p36 and defines the shortest region of overlap. Black boxes represent LOH, gray boxes are non-informative loci, white boxes are retained heterozygosity, and hatched boxes indicate microsatellite mutations.

Table 4: 15 : Detail of 38 Neuroblastoma tumors LOH deletions of chromosome 1

Basic results (Table 4)

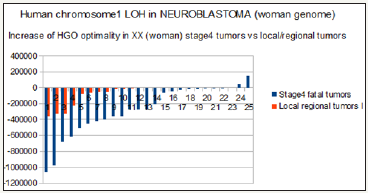
To conclude: Recall that chromosome 1 is downstream with respect to the tipping point HGO (see manuscript Figure 3). Therefore, by virtue of our “global LOH strategy law by chromosomes”, most LOHs “should” improve the HGO value: indeed, 36 out of 38 cases increase HGO as well in the case of (XX) than in the case of a male genome (XY).

Conclusion

15 Glioblastoma tumors LOH in chromosome 10

Glioblastoma is a particularly dangerous brain cancer. Glioblastoma (World Health Organization [WHO] Grade IV) is the most frequent and malignant human brain tumor, occurring at a frequency of two to three cases per 100,000 population and per year for most European and North American countries.

Based on this same publication [22], we studied 15 cases of tumors involving LOH deletions of chromosome 10. These 15 cases are subdivided into 8 cases of primary glioblastomas characterized by deletions covering the p and q arms of chromosome 10, whereas the 7 other cases affect only the q arm. Paradoxically, they cause secondary glioblastomas that are more pathogenic than the primaries. Analysis by our HGO law demonstrates that since chromosome 10 is downstream of the HGO swapping point (Figure 3), this second category of deletions is more pathogenic than the first one in that it optimizes 1.20 times more LOH (Figure 11).

Figure 8: The case analyzed from Figure 1 in publication [22]

Figure 9: The case analysed from Figure 3 in publication [24]

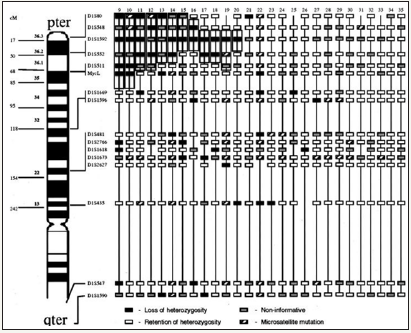
Figure 10: the case analysed from Figure 4 in publication [24].

Figure 11: Human chromosome 10 in glioblastoma : HGO optimality increased 1.2 between primary (left) and secondary (right) grade tumors.

38 Neuroblastoma tumors LOH in chromosome 1

Figure 12: Evidence of an increase HGO (Human Genome Optimality) between local and regional tumors and stage 4 high pathogenic tumors in the case of male (XY) NEUROBLASTOMA chr1 LOH tumors.

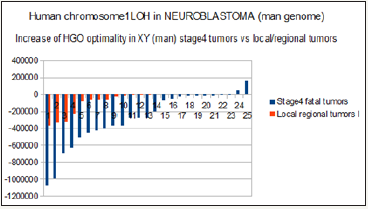
Neuroblastoma is a very complex form of brain cancer, often involving LOH on several chromosomes. A very pathogenic form is based on LOHs of chromosome 1p. From this published paper [24], we studied and then compared respectively the evolution of the HGO for 13 LOH of local / regional tumors, then 25 other LOHs of highly pathogenic stage 4 tumors. Out of 38 cases analyzed, 36 increase the optimality of HGO. In the case of stage 4 tumors, the average increase in HGO optimality is 2.3 times higher than that of the 13 local / regional tumors. Figure 12 & Figure 13 analyze these HGO evolutions according to whether the genomes studied are those of a male XY (Figure 12) or a female XX (Figure 13).

Figure 13: Evidence of an increase HGO (Human Genome Optimality) between local / regional tumors and stage 4 highly pathogenic tumors in the case of female (XX) NEUROBLASTOMAS chr1 LOH tumors.

Finally, on 53 cases of LOH mutations analyzed for the two types of Glioblastoma and neuroblastoma cancers, the HGO optimality law is verified in 50 cases and in failure for only 3 cases, ie a percentage of validity of this universal law equal to 94.24. %.

About universality of HGO law relating to chromosomal LOH deletions of tumors

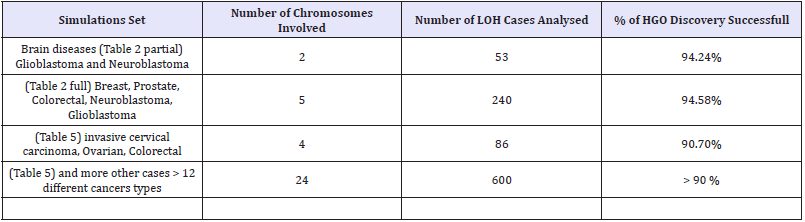
In a more exhaustive but informal analysis of more than 600 LOH deletions, we wanted to verify the universality of this law unifying the LOH associated with various tumors. For this, we analyzed several dozen types of tumors exclusively from peer review publications and affecting almost all of the 24 human chromosomes. This short sampling of 4 independent examples confirms the UNIVERSALITY of the law set out throughout this article : >90% success of the generic law on 86 LOH cases related to chromosomes 18, 2, 17 and 22 LOH deletions (Table 5).

Table 5: Four sample examples from the 600 LOH large scope analysis demonstrating the UNIVERSALITY of the LOH deletions HGO law.

This short sampling of 4 independent examples confirms the UNIVERSALITY of the law set out throughout this article.

Table 6: Universality of HGO discovery.

Finally, the Synthetic Table below Demonstrates the UNIVERSALITY of HGO Discovery (Table 6)

General considerations on this theoretical human genetic optimum (HGO) of (3 – Phi) / 2: This formula is particularly simple. We can even make it more “beautiful”, indeed

Since 1 + Phi = Phi * 2, we can write:

(3 – Phi)/2 = C +G/T + A = (4 − (1+ Phi))/2 = (4 − (Phi*2)) 2 = (2*2 − Phi*2)/2 = C+G/T+A

This new equivalent formula contains only the numbers “2” and “Phi”: A second track to be studied could consist in replacing this writing by:

By this artifice of writing, we thus make the “3” appear in the numerator and the denominator (!)

(3− Phi)/2=(3−Phi)/(5−3)=C+G/T+A

The formula then becomes:

(3−Phi)x(T+A)=2x(C+G)=(5−3)x(C+G)

3(T+A)+3(C+G)=5(C+G)+Phi(T+A)

3(T+A+C+G)=5(C+G)+Phi(T+A)

Therefore, if we consider that the single copy (single strand DNA) of the 24 chromosomes whole genomes XX or XY all lead to the same attractor HGO = (3-Phi) / 2, to write :

Considering the cumulative population of 24 chromosomes of the single human genome (single strand DNA),

We check the following perfect balance

“THREE times the whole genome

“(T+A+C+G)=FIVE _times(C+G)PLUS _{Phi times}(T+A)

Verification on 24 hg38 chromosomes single strand DNA:

CG = 1200551672

TA = 1737087441

3×(CG+TA) = 8812917339

(5×CG)+(PHI×TA) = 8813424881

8812917339÷8813424881 = 0.9999424126

8812917339-8813424881 = ¯507542

Finally, it is remarkable that this formula is based on integers 3 or 5. In fact, these numbers are very small integers and they are Fibonacci numbers. It will therefore be interesting to postpone the error calculations on the accuracy of these two integers 3 and 5:

(5×CG)+(Phi×TA) = 8813424881

(CG+TA) = 2937639113

8813424881 / 2937639113 = 3.000172772

and

3×(CG+TA) = 8812917339

-

(Phi×TA) = 2810666521

8812917339 -2810666521 = 6002250818

CG = 1200551672

6002250818÷CG = 4.999577243

The exact formula can then be written:

3.000172772 (T+A+C+G) = 5(C+G) + Phi(T+A)

or

3(T+A+C+G) = 4.999577243 (C+G) + Phi(T+A)

We still have à lot to discover on this fascinating CODE that is DNA

To conclude, it is difficult to fully understand the extent of this discovery:

a. At the theoretical level it seems fascinating that there exists this perfect digital fit of the whole genome around this sort of digital attractor.

b. At the theoretical level again, one will note the universality of the HGO law, which applies to ALL the cancers.

c. At the applied level, the correlation between this law and the increasing degrees of pathogenicity of the tumors is remarkable. It is thus well understood that the mechanism of invasive pathogenicity of a tumor is because its genome is more optimal than that of a healthy cell ...

d. Its immediate application is the prioritization of tumor pathogenicity stages.

In this study we have just raised a new corner of sail on DNA and the human genome.

A jump was the discovery of the fractal nature of DNA [2,28] or certain structures of the brain [29]. Thus, mathematics has become imbedded in genetics. Other mathematical approaches to genomes, which are equally original, are to be noted with approaches to matrix [30] or mathematical topology [31]. Then it is frankly an hypothetical « quantum theory of DNA information» that invites itself into DNA [32].

And, of course, there is the famous golden ratio and its Fibonacci numerical patterns. They’re not only found in the rhythms of the heart and in the arborescence of our arteries [33], but also in the RNA [34] or in quantum physics [35].

Finally, like these different researchers, we have just demonstrated how the “CODES” [36] are at the heart of the mechanisms of Nature ... “Codes” real today ... “Codes” artificial tomorrow [37].

As demonstrated in [38], a substantial fraction of mutations in human cancer are attributable to random errors occurring during DNA replication. Therefore, we think that our « long range human genome law » controling cancer mutations is probably important.

In [5,39,40-49] we will present other “hidden mathematical codes” that organize the DNA sequences of the human genome.

However, the major conclusion seems to be the following

All the human genetic heritage is concentrated in 2 genomes: the nuclear genome and its 23 pairs of chromosomes on the one hand, and the small mitochondrial genome mtDNA, on the other hand.

The majority of mutations associated with genetic diseases as well as all cancers most often lead to deletions affecting each of these 2 genomes.

Then, in the article “Sapiens mtDNA circular long-range numerical meta-structures are High correlated with mtDNA diseases mutations” [39], as in the present article, we demonstrate that all these mutations unbalance, for both genomes, a kind of optimum of each of these genomes.

This is probably the major result that we will have to continue to reflect on and experiment with Finally, our approach may be related to these hundreds of unpredictable mutations resulting from manipulation of genomes by CRISPR revolutionary technology [43]. Effectively in their 2017 article, authors note that « …/...They found that the technique had successfully corrected a gene that causes blindness in the mice, but the two mice that had undergone CRISPR gene-editing had sustained more than 1,500 unintended single-nucleotide mutations, and more than 100 larger deletions and insertions …/...».

Acknowledgements

We especially thank Dr. Robert Friedman M.D. practiced nutritional and preventive medicine in Santa Fe, New Mexico, worldwide expert on Golden ratio Life applications. We also thank the mathematician Pr. Diego Lucio Rapoport (Buenos aires), Marco F. Paya Torres (M.D Alicante), the french biologist Pr. François Gros (Pasteur institute,co-discoverer of RNA messenger with James Watson and Walter Gilbert ), Professor Sergey V. Petoukhov (Dr. Phys.Math.Sci, Grand Ph.D., FullProfessor, Laureate of the State prize of the USSR), Volkmar Weiss (Dr. rer. nat. habil. Dr. phil. Habil. Leipzig, Germany), and Pr. Luc Montagnier, medicine Nobel prizewinner for their interest in my research of biomathematical laws of genomes.

References

1. Suzuki K, Tsunekawa Y, Hernandez-Benitez R, Wu J, Zhu J, et al. (2016) In vivo genome editing via CRISPR/Cas9 mediated homologyindependent targeted integration. Nature 540(7631): 144-149.
2. Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, et al. (2009) Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326(5950): 289-293.
3. Perez JC (1991) Chaos DNA and neuro-computers: a golden link. Speculations in Science and Technology 14: 336-346.
4. Marcer PJ (1992) Order and chaos in DNA - the Denis Guichard Prizewinner: Jean-Claude Perez. Kybernetes 21: 60-61.
5. Perez JC (1997) L’adn Décrypté. Resurgence publisher Liege, Belgium.
6. Perez JC (2009) Codex Biogenesis. Resurgence, Liege Belgium.
7. Šmarda P, Bureš P, Horová L, Leitch IJ, Mucina L, et al. (2014) Ecological and evolutionary significance of genomic GC content diversity in monocots, PNAS 111(39): E4096-E4102.
8. Bernardi G (2007) The neoselectionist theory of genome evolution. Proc Natl Acad Sci USA 104(20): 8385-8390.
9. Bernardi G (2000) Isochores and the evolutionary genomics of vertebrates. Gene 241(1): 3-17.
10. Perez JC (2010) Codon Populations in Single-Stranded Whole Human Genome DNA Are Fractal and Fine-Tuned by the Golden Ratio 1.618. Interdiscip Sci 2(3): 228-240.
11. Perez JC (2011) Caminos Interdisciplinaios. Seminario CLAVE_INTER, Espacio Interdisciplinario, Universidad de la Republica Montevideo, Uruguay.
12. Perez JC (2011) Decoding Non-Coding DNA Codes: Human Genome Meta-Chromosomes Architecture. BIT Life Sciences’ 3rd Annual World Vaccine Congress, Beijing, China.
13. Perez JC (2013) The “3 Genomic Numbers” Discovery: How Our Genome Single-Stranded DNA Sequence Is “Self-Designed” as a Numerical Whole. Applied Mathematics 4(10B): 37-53.
14. Perez J (2015) Deciphering Hidden DNA Meta-Codes -The Great Unification & Master Code of Biology. J Glycomics Lipidomics 5: 131.
15. Perez JC Fractal Self-similarity, Scale Invariance and Stationary waves Codes Architecture Human Chromosomes DNA sequences 1(1).
16. Neanderthal genome (2014).
17. Sapiens Build34 (2003) genome.
18. Sapiens HG38 (2013) genome.
19. Venter JG, Telenti A, Pierce LC, Biggs WH, di Iulio J, et al. (2016) Deep Sequencing of 10,000 Human Genomes Proc Natl Acad Sci U S A 113(42): 11901-11906.
20. Eiriksdottir G, Johannesdottir G, Ingvarsson S, Björnsdottir IB, Jonasson JG, et al. (1998) Mapping loss of heterozygosity at chromosome 13q: loss at 13q12-q13 is associated with breast tumour progression and poor prognosis. Eur J Cancer 34(13): 2076-2081.
21. Johannsdottir HK, Jonsson G, Johannesdottir G, Agnarsson BA, Eerola H, et al. (2006) Chromosome 5 imbalance mapping in breast tumors from BRCA1 and BRCA2 mutation carriers and sporadic breast tumors. Int J Cancer 119: 1052-1060.
22. Fujisawa H, Reis RM, Nakamura M, Colella S, Yonekawa Y, et al. (2000) Loss of Heterozygosity on Chromosome 10 Is More Extensive in Primary (De Novo) Than in Secondary Glioblastomas, Laboratory Investigation 80(1): 65-72.
23. Lengauer C Thiagalingam S, Laken S, Willson JK, Markowitz SD, et al. (2001) Mechanisms underlying losses of heterozygosity in human colorectal cancers, Proc Natl Acad Sci U S A 98(5): 2698-2702.
24. Mora J, Cheung NK, Kushner BH, LaQuaglia MP, Kramer K, et al. (2000) Clinical Categories of Neuroblastoma Are Associated with Different Patterns of Loss of Heterozygosity on Chromosome arm 1p. J Mol Diagn 2(1): 37-46.
25. Latil A, Cussenot O, Fournier G, Driouch K, Lidereau R et al. (1997) Loss of heterozygosity at chromosome 16q in prostate adenocarcinoma: identification of three independent regions. Cancer Res 57(6): 1058- 1062.
26. Wolf-Hirschhorn syndrome, in Genetics Home Reference, NIH U.S. National Library of Medicine, USA.
27. Friedman R, Cross M (2013) The Golden Ratio & Fibonacci Sequence: Golden Keys to Your Genius, Health, Wealth & Excellence. (1st edn), Hoshin Media, USA.
28. Pellionisz AJ, Graham R, Pellionisz PA, Perez JC (2012) Recursive Genome Function of the Cerebellum: Geometric Unification of Neuroscience and Genomics. In: Manto M & DL, et al. (Eds.), Handbook of the Cerebellum and Cerebellar Disorders. (1st edn), Springer, USA.
29. Dokukin ME, Guz NV, Woodworth CD, Sokolov I (2015) Emergence of fractal geometry on the surface of human cervical epithelial cells during progression towards cancer. New J Phys 17(3).
30. Petoukhov S (2011) Mathematics of Bioinformatics: Theory, Methods and Applications. (1st edn), John Wiley & Sons, USA.
31. Rapoport DL (2015) Klein Bottle Logophysics, Self-reference, Heterarchies, Genomic Topologies, Harmonics and Evolution. Part III: The Klein Bottle Logic of Genomics and its Dynamics, Quantum Information, Complexity and Palindromic Repeats in Evolution , Quantum Biosystems 7(1): 107-174.
32. Montagnier L, Aïssa J, Capolupo A , Craddock TJA , Kurian P, et al. (2017) Water Bridging Dynamics of Polymerase Chain Reaction in the Gauge Theory Paradigm of Quantum Fields, Water 9(5): 339.
33. Dharam P, O’Leary, James P (2015) Fibonacci Series, Golden Proportions, and the Human Biology HWCOM Faculty Publications. Paper 27, USA.
34. Hengwu Li, Daming Zhu, Zhang C, Han H, Crandall KA (2014) Characteristics and Prediction of RNA structure. BioMed Research International Article ID 690340.
35. Vaezi A, Barkeshli M (2014) “Fibonacci Anyons From Abelian Bilayer Quantum Hall States.” Physical Review Letters 113.
36. Marshall P (2015) Evolution 2.0. Benbella Books, USA.
37. Yampolskiy RV (2017) On the origin of synthetic life: attribution of output to a particular algorithm. Physica Scripta 92(1).
38. The Royal Swedish Academy of Sciences (2017) Phys Scr 92.
39. Tomasetti C, Lu Li, Vogelstein B (2017) Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention. Science 355(6331): 1330-1334.
40. Perez JC (2017) Sapiens Mitochondrial DNA Genome Circular Long Range Numerical Meta Structures are Highly Correlated with Cancers and Genetic Diseases mtDNA Mutations. J Cancer Sci Ther 9: 512-527.
41. Perez JC (2017) DUF1220 Homo Sapiens and Neanderthal fractal periods architectures break through SDRP Journal of Cellular and Molecular Physiology 1(1).
42. Perez JC (2017) Humans and Primates Chromosomes4 Fractal CODES: periodic stationnary waveforms charaterizing and differenciating Neanderthal and Sapiens whole chromosomes DNA sequences.
43. Perez JC (2017) Symmetry and Asymmetry in the MENDELEEV’s Periodic Table Predictive Equation. SDRP Journal of Computational Chemistry & Molecular Modelling 2(1).
44. Schaefer KA, Wu WH, Colgan DF, Tsang SH, Bassuk AG, et al. (2017) Unexpected mutations after CRISPR-Cas 9 editing in vivo, Nature Methods. Nature Methods 14: 547-548.
45. Perez JC (2017) Decyphering “the MASTER CODE ®” Structure and Discovery of a Periodic Invariant Unifying 160 HIV1/HIV2/SIV Isolates Genomes. Biomed J Sci & Tech Res.
46. Perez JC (2017) The “Master Code of DNA”: Towards the Discovery of the SNPs Function (Single-Nucleotide Polymorphism). J Clin Epigenet 3(3): 26.
47. Perez JC (2017) The “Master Code of Biology”: Self-assembly of two identical Peptides beta A4 1-43 “Amyloid” in Alzheimer’s Diseases. Biomed J Sci & Tech Res 1(4)-2017.
48. Perez JC (2017) The «Master Code of Biology»: from Prions and Prionslike Invariants to the Self-assembly Thesis. Biomed J Sci & Tech Res 1(4)- 2017.
49. Perez JC (2017) Why the genomic LOCATION of individual SNPs is FUNCTIONAL? (2017)SDRP Journal of Cellular and Molecular Physiology 2(1).