Resolving the Controversial Issues and Optimal New Protocols for Accelerated Corneal Cross-Linking (CXL)

Corneal collages cross-linking (CXL) is a clinical procedure using UVA light (at 365nm) to activate riboflavin solution causing biomechanical properties change of the corneal stroma for the treatment of keratoconus, or producing free oxygen radicals to treat corneal ulcers. Other potential applications include the reduction of postoperative regression in vision correction and scleral treatment in malignant myopia, scleromalacia and low tension glaucoma. The first animal data was reported by Wollensak [1] in 2003 for the treatment of keratoconus. Extensive clinical aspects of CXL have been covered in a recent book edited by Hafezi and Randleman [2]. The theoretical aspects of CXL analyzing the kinetics and fundament formulas have been developed by Lin [3-13]. This Editorial Review will address the current controversial issues in CXL with possible theoretical resolutions. It will also update (with greater details) the new protocol called controlled-concentration-method (CCM) proposed by Lin [11].

The controversial issues to be discussed include:

A. Safety criteria (and the minimum corneal thickness

B. Dynamic profiles and depletion of riboflavin

C. Validation of Bunsen Roscoe law (BRL)

D. UV light Intensity cutoff maximum and minimum exposure time

E. The role of oxygen and pulsed mode

F. CXL efficacy (type-I and type-II)

G. Dresden vs. Modern protocols

H. Demarcation line depth vs. CXL efficacy

New safety criteria [3,7]

The conventional accepted safety criteria for minimum corneal thickness z*=400um, for a dose of 5.4J/cm2, proposed by Wollensak et al. [1] was meaningless without specifying the riboflavin (RF) concentration, C0, and its profile, besides its underestimated the endothelium damaged threshold (Ed) at least a factor of 8 according to the clinical data of Mooren et al. [14]. The minimum corneal thickness formula is given by [7] z=(1/A) [2.2+ln(E/E’)], where A is an effective absorption given by A=290m(1-0.25z/D) C0+32 (with fit parameter m). We note that z is a decreasing function of C0 and D and increasing function of the UV dose ratio E/Ed, At the referenced point, E=E’, z*=400um, as expected. The conventional safety criteria [1], E=5.4J/cm2 and z=400um, is just one of the special case, for Ed=0.35mW/cm2 (under the Dresden protocol) and cannot be the safety standard.

Dynamic profiles

Conventional modeling [15-18] assumed a constant RF concentration during the crosslink, which is true only under the so-called Dresden protocol [1,2], in which the RF is constantly resupplied to compensate its depletion. However, it also reduced the available effective dose to approximately about 70% to 80% of the applied dose 5.4J/cm2. The constant-RF also underestimated the UV light intensity, which in general, is an increasing function of time (when RF depletion is included), given by [5,6] I(z,t)=I0 exp[-A(z,t)] with A(z,t) is a decreasing function of time when C(z,t) is depleted, given by A(z,t)=2.3[(a-b)C(z,t)G(z)+bC0]+Q, where a,b and Q are, respectively, the absorption constant of RF, photolysis product and stroma (without RF); G(z)=1-0.25z/D; and F(z)=1-0.5z/D is the initial RF distribution defined by a diffusion constant (D) [6].

The dynamic profiles of RF and concentration and UV light intensity are shown, where C(z,t) is a decreasing function (depletion) of time, whereas I(z,t) is an increasing function of time due to reduced absorption, A(z,t). Crosslink time, T*(z,t), defined by the when C(z,t) is depleted to 0.13, and is given by T*=T0 exp(Az), with the surface value T0=258/I0. Lin also defined a crosslink depth (z*) when the CXL efficacy reaching it maximum, given by z*=ln (NE0)/A, with N=0.16 (for D>>1cm) and N=0.224 (for D=500um). We note that z* is an increasing function of the UV dose, but decreasing function of A and C0.

The UV light intensity increases from its initial value I(z,t)=I0 exp[-A1z] to steady-state vale given by I(z,t)=I0 exp[-A2z], with 0 0 A1 = 2.3aC +Q, A2 = 2.3bC +Q . For C0=0.1%, a=204 (1/cm/%), b=50 (1/cm/%), and Q=32 (/cm), we obtain A1=79 (1/cm), and A2=43.5 (1/cm), with an averaged value of 61 (1/cm), which are much larger than the RF-constant model with a value of 42.5 (1/ cm). If one assumes Q=b=0, then A=46.9 (1/cm), which is smaller than our averaged value of 61 (1/cm). Numerical simulation of Lin and Cheng [6], also showed another fit A=2.3[mbC0 + Q], with m=1.5 for b=50(1/%/cm), which is fit to the CXL efficacy (at steady state). In this fitting, (for D=500um), A=49 and 66 (1/cm) for C0=0.1% and 0.2%.

Validation of Bunsen roscoe law (BRL)

To shorten the CXL treatment duration while maintaining the similar CXL efficacy, accelerated CXL (AXL) protocols have been proposed to replace the Dresden low-power protocol based on the BRL of reciprocity [19] stating that the effect of a photo-biological reaction is proportional only to the total irradiation dose (E=It), or the product of intensity (I) and exposure time (t). To achieve the same efficacy, the required exposure time based on BRL is given by t=E/I, which gives the protocol for AXL; for example, t= (30, 10, 5, 3,2) minutes for I= (3,9,18,30,45) mW/cm2. Validation of BRL has been challenged by Lin’s non-linear law and the S-formulas for CXL efficacy [6,7,10]. Wernli et al. [17] also pointed out the limitation of BRL due to the sudden drop of efficacy at UV intensity around 45mW/cm2. To improve the CXL efficacy, extended exposure time and/or dose, has been proposed [20,21] to compensate the drawback of exposure time predicted by BRL. Moreover, a concentration-controlled method (CCM) was proposed by Lin [11] to improve the CXL efficacy by resupply of RF during the UV exposure.

The role of oxygen and pulsed mode

CXL efficacy is governed by both oxygen-mediated (OM) and non-oxygen-mediated (NOM) 3-pathway processes, rather than the conventionally believed type-II only (oxygen-mediated) mechanism [9,10]. Both type-I and type-II reactions can occur simultaneously, and the ratio between these processes depends on the type of photosensitizers (PS) used, the concentrations of PS, substrate and oxygen, the kinetic rates involved in the process, and the light intensity, dose, PS depletion rate etc. The CXL 3-pathway kinetics maybe described as follows. For type-I, the riboflavin triplet state [T] may interact directly with the stroma collagen substrate [A] under NOM (with a rate constant k8, pathway-1); or with the ground-state oxygen [3O2] to form reactive oxygen species [O-] under OM; and in type-II process, [T] interacts with [3O2] to form a singlet oxygen [1O2]. [T] may also relax to riboflavin ground state (with a rate constant k5). Both reactive oxygen species (ROS), [O-] and [1O2], can either relax to [3O2], or interact with [A] for crosslinking.

Figure 1:Schematics of the oxygen concentration profiles in CXL; in the transient stage, both type-I and type–II coexist until the oxygen is depleted; then type-I dominates before the oxygen is replenished [9,10].

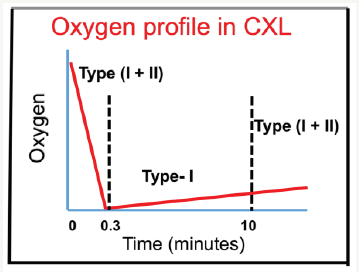
Schumacher et al. [15] reported the NOM-type-I CXL, in contrast to Kling et al. [22] claiming that oxygen-mediated type-II played the critical role of CXL efficacy. Furthermore, Kamaev et al. [18] claimed that CXL is NOM-type-I dominant, while the OM-type-II only plays a limited and transient role, as shown by Fig. 2. If Kling et al. [5] were correct, then all the reported results of epi-on CXL would not be possible, since only limited and transient oxygen supply is available. Lin [9,11] proposed mathematical model in supporting the claims of Kamaev et al. [18]. Pulsed mode was claimed to have higher efficacy than CW mode [22]. This conclusion, I believe, is due to clinical measured errors and/or non-controlled comparison of RF concentration during the UV exposure, based in Lin & Kamaev studies [9,18] that OM-type-II only plays a limited and transient role. As shown by (Figure 1), the role of oxygen resupply (and pulsed mode) takes few minutes. Therefore, pulsing in few seconds would not help the Type-II efficacy.

Dresden vs. modern protocols

The standard Dresden (SD) protocol was proposed by Wollensak et al. [2] in 2003, where a UVA light (at 365nm) was used to treat cornea 9mm zone at an intensity of 3.0mW/cm2 for 30 minutes, delivering a fluence (dose) of 5.4J/cm2. Modern protocols, named as CCM by Lin [11], used a limited resupply of RF to eliminate the extra blocking effect due to over resupplied RF in Dresden protocol. CXL efficacy is influenced by multiple factors including, the UV light intensity, exposure period and dose, the initial concentration profiles of RF and oxygen, the quantum yield of the RF triplet state, the kinetic rate constants of RF (in type-I) and oxygen (in type-II).

Besides, the protocol procedures defining how the RF drops are applied pre-operatively and during the UV exposure are also important, because they define the initial, and intra-procedure RF concentration profiles (or diffusion depth). For example, the frequency of RF drops (Fdrop) applied on the cornea after the UV is turned on, and the waiting period (Twait) for each RF drops instillation during the UV exposure. In the conventional Dresden protocol, Fdrop is about 5 to 10 times and Twait=0. In contrast, our proposed concentration-controlled method (CCM) uses Fdrop =2 to 4 (for RF replenishment) and Twait is 1 or 2minutes (for enough diffusion depth, with D>150um). Kling et al. [23] recently reported the use of 1.5mW/cm2 intensity for 30 minutes exposure (or 2.7J/ cm2 dose) has similar efficacy as that of 3mW/cm2 and 30 minutes exposure (5.4J/cm2 dose). This feature may be easily realized by our S-function which has an optimal dose predicted to be about 3 to 4J/cm2, and the 5.4J/cm2 (for 3mW/cm2) is certainly higher than the optimal value proposed by Lin’s CCM [9,11].

Cut-off maximum intensity

Controversial results for the corneal cross-linking (CXL) efficacy in standard low-power Dresden-CXL (DXL) and accelerated-CXL (AXL) have been reported [24-27]. In addition, various maximum (cutoff) UV light intensities were clinically reported by Hammer et al. [25] (18mW/cm2), Webb et al. [26] (34mW/cm2), Bao et al. [27] (30mW/cm2), and Wernli et al. [17] (45mW/cm2). Webb et al. [26] believed that AXL has a shallower crosslink depth which results a lower efficacy in AXL than DXL. However, in most reported protocols, even similar pre-operative RF drops administration were performed, significant different cutoff light intensity and CXL efficacy were still observed [24-27]. Therefore, further analysis based on influencing factors during the UV exposure, other than the pre-operative Rf condition, are required. Bao et al. [27] and O’Brart et al. [28] reported that higher efficacy can be achieved by using a higher RF concentration, in consistent with the predicted role of Rf concentration by Lin [12].

CXL efficacy

Figure 2:Efficacy vs. light intensity from clinical data of Wernli et al. [17] (triangles), Hammer et al. [25] (cubic), Bao et al. [27] (bar), and Webb et al. [26] (circle).

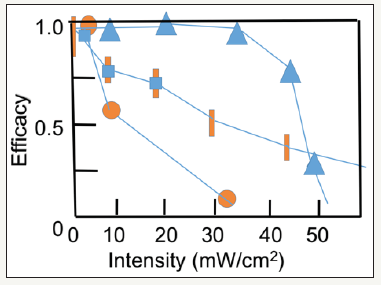
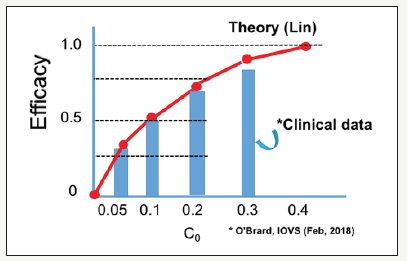
The type-I CXL efficacy is given by [6] Eff=1-exp(-S), where the S-function is proportional to (FC0/I0)0.5 exp(0.5Az), or (for z=0) and stronger dependence of (for z>0), because A is also proportional to C0. given by ( ) 0 A = 290m 1− 0.25z / D C + 32 (with fit parameter m). Figure 2 shows the efficacy vs. light intensity from clinical data of Wernli et al. [17] (triangles), Hammer et al. [25] (cubic), Bao et al. [27] (bar), and Webb et al. [26] (circle). (Figure 3) shows the CXL efficacy versus riboflavin concentration shows the nonlinear feature, where theoretical curve (red curve) is compared with the clinical data (bars) of O’Brart et al. [28] (Figure 2 & 3).

Figure 3:CXL efficacy versus riboflavin concentration shows the nonlinear feature, where theoretical curve (red curve) is compared with the clinical data (bars) of O’Brart et al. [28].

Update on lin’s CCM

The intrinsic efficacy drawbacks of AXL, under a non-controlled situation in Dresden protocols, may be overcome by a newly proposed protocol called controlled-concentration-method (CCM) by Lin [11], in which extra Rf drops are applied to the cornea, at every crosslink time (T*), during the UV exposure, having a frequency defined by Fdrop=N-1, with N= 0.365 [I0/C0]0.5, where N=2, for the referenced point with I0=3mW/cm2 and C0=0.1%. Therefore, Fdrop = (1, 2, 4, 5, 7), for I0 = (3, 9, 18, 30, 45) mW/ cm2 and for C0=0.1%; which reduced to Fdrop = (1, 1, 2, 3, 4), for higher C0=0.3%. Given Fdrop=N-1, the combined efficacy defined as c −Ceff =1− exp −(S1 + S2 + …Sj) , with j=N=Fdrop+1. The above Fdrop plays the critical factor influencing the CXL efficacy. Therefore, comparison of DXL and AXL without specifying the exact Fdrop-protocol is questionable. WE note that in the CCM, the time to resupply Rf drops is given by T* which is a deceasing function of the light intensity. In comparison, the Dresden protocol (DXL), Rf drops were continuously administrated during the UV exposure, every 3 to 5minutes, a fixed time regardless the light intensity.

For a low intensity (3mW/cm2) in DXL, the total exposure time is 30 minutes, therefore it has Fdrop= 6 to 10, which is overdone and will reduce the effective dose approximately 25% to 30% out of the 5.4J/cm2. In the protocol of Bao et al. [27] and Webb et al. [26], they did not resupply any Rf drops in their high intensity studies, corresponding to Fdrop=0 (or N=1). Therefore, their concluded comparison between DXL and AXL did not have a fair reference, and their AXL efficacy is lower than what are predicted by CCM, which has the maximum efficacy for AXL. The results of Spadea et al. [20,21], based on resupply of Rf drops (during the UV exposure) every 3 and 5 minutes, which showed similar efficacy of 3 and 9mW/cm2. Lin’s S-formulas also demonstrates that epi-on CXL (having a smaller D and C0) is less efficient than epi-off CXL, in consistent with reported data of Spadea et al. [20].

Crosslink volume

A new CXL efficacy was proposed by Lin [12] given by the product of [strength] (or the maximal value of S) and the [depth] (or z*), i.e., the volume of stroma being cross-linked. It should be noted that deeper CXL (or larger z*) may be achieved by larger fluence (E0), i.e, more superficial CXL in higher C0 may be compensated by larger light-dose. However, considering optimal CXL with minimal UV exposure time (or dose), one requires an optimal range of C0- 0.15% to 0.3% and and 2 E₀ = 3.5 to 4.5 J / cm , such that [depth] z*=200 to 300um, with [strength] S1=1.5 to 2.0 (or CXL efficacy 1-exp(-S1)=0.78 to 0.86), noting that high C0 causes a competing of [strength] and [depth] which needs to be optimized. Greater detail with numerical simulation will be presented elsewhere.

Demarcation line depth and CXL efficacy

Spadea et al [20,21] studied the relationship between CXL efficacy and the UV light exposure duration, intensity, and the demarcation line (DL) depth based on available measured data. They concluded that the duration of the procedure might be the rate-limiting step in the efficacy of CXL. The sudden-drop of DL depth at high intensity (>45mW/cm2) has the similar feature as the AXL efficacy reported by Wernli et al. [17]. However, it is clinically unclear whether DL depth is proportional to the crosslink depth or the CXL efficacy. Moreover, controversial results of AXL efficacy were reported due to inconsistent protocols which were not optimized.

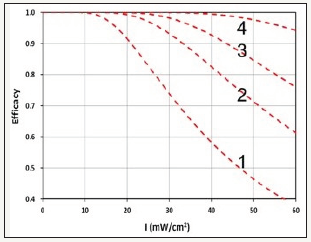
The measured DL depth may be compared with a combined CXL efficacy given by c-Ceff=1-exp (-4R), with , where F(z)=1-0.5z/D, is the Rf initial concentration profile defined by a diffusion depth (D); t’ is the resupply Rf drops every t’-minutes. R is the efficacy ratio between the non-controlled Dresden protocol and the optimal protocol (via CCM) having R=1.0, and c-Ceff=0.98, for all range of UV intensity I0=3 to 60mW/cm2. Figure 2 shows the theoretical Curves (1,2,3,4) calculated from the combined efficacy (c-Ceff) formula, with time of resupply Rf drops t’= (4,2,1,0.5) minutes; noting that smaller t’ associated with larger Fdrop, therefore, has higher efficacy.

(Figure 4) may be compared with (Figure 2) (measured efficacy data). Comparing the theoretical curves and the measured DL depth, one may conclude that CXL efficacy is proportionally related to the DL depth, and both have a cutoff maximum intensity, under the non-controlled Dresden protocol, as reported by Wernli et al. [4]. It should be noted that the theoretical Curve-4 (with t’=0.5 minutes, or Fdrop=3) gives the optimal efficacy similar to CCM [11] (Figure 4).

Figure 4:Theoretical CXL efficacy vs. UV light intensity for resupply of RF drops at various time, t’ = (4,2,1,0.5) minutes, for Curves (1,2,3,4).

We have presented the resolutions of controversial issues in CXL via factors influencing the CXL efficacy. To improve the efficacy of ACXL, a CCM was proposed. A new CXL efficacy defined by the product of [strength] (or the maximal value of S) and the [depth] (or z*), i.e., the volume of stroma being cross-linked is introduced. CXL efficacy is proportionally related to the DL depth, and both have a cutoff maximum intensity.

1. Wollensak G, Spoerl E, Wilsch M, Seiler T (2003) Endothelial cell damage after riboflavin-ultraviolet-A treatment in the rabbit. J Cataract Refract Surg 29(9): 1786-1790.
2. Hafezi F, Randleman JB (2016) Corneal collagen cross-linking. Slack Inc, NJ, USA.
3. Lin JT (2015) Analytic formulas on factors determining the safety and efficacy in UV- light sensitized corneal cross-linking. Invest Ophthalmol Vis Sci 56: 5740-5741.
4. Lin JT (2015) On the dynamic safety for cross linking in thin corneas (350-398 um) with extra protection under a contact lens. J Refract Sur 31(7): 495-496.
5. Lin JT, Cheng DC, Chang C, Yong Zhang (2015) The new protocol and dynamic safety of UV-light activated corneal collagen cross-linking. Chinese J Optom Ophthalmol Vis Sci 17: 140-147.
6. Lin JT, Cheng DC (2017) Modeling the efficacy profiles of UV-light activated corneal collagen crosslinking. PloS One 12: e0175002.
7. Lin JT (2017) Efficacy and Z* formula for minimum corneal thickness in UV-light crosslinking. Cornea 36(11): 30-31.
8. Lin JT (2017) Photochemical Kinetic modeling for oxygen-enhanced UVlight- activated corneal collagen crosslinking. Ophthalmology Research 7(1): 1-8.
9. Lin JT (2018) Efficacy S-formula and kinetics of oxygen-mediated (type-II) and non-oxygen-mediated (type-I) corneal cross-linking. Ophthalmology Research 8(1): 1-11.
10. Lin JT (2018) A Critical review on the kinetics, efficacy, safety, nonlinear law and optimal protocols of corneal cross-linking. J Ophthalmology & Visual Neuroscinece 3: 017.
11. Lin JT (2018) A proposed concentration-controlled new protocol for optimal corneal crosslinking efficacy in the anterior stroma. Invest Ophthalmol Vis Sci 59(1): 431-432.
12. Lin JT (2018) The role of riboflavin concentration and oxygen in the efficacy and depth of corneal crosslinking. Invest Ophthalmol Vis Sci 59 (in press).
13. Lin JT (2018) Corneal Collagen Cross-linking (CXL): Controversy and Fundamentals. Ophthalmol Clin Res 1(1): 17-21.
14. Mooren P, Gobin L, Bostan N, Wouters K, Zakaria N, et al. (2016) Evaluation of UVA cytotoxicity for human endothelium in an ex vivo corneal cross-linking experimental setting. J Refract Surg 32((1): 41-46.
15. Schumacher S, Mrochen M, Wernli J, Bueeler M, Seiler T (2012) Optimization model for UV-riboflavin corneal cross-linking. Invest Opthamol Vis Sci 53(2): 762-769.
16. Kling S, Hafezi F (2017) An algorithm to predict the biomechanical stiffening effect in corneal cross-linking. J Refract Surg 33(2): 128-136.
17. Wernli J, Schumacher S, Spoerl E, Mrochen M (2013) The efficacy of corneal cross-linking shows a sudden decrease with very high intensity UV light and short treatment time. Invest Ophthalmol Vis Sci 54: 1176- 1180.
18. Kamaev P, Friedman MD, Sherr E, Muller D (2012) Photochemical kinetics of corneal cross-linking with riboflavin. Invest Ophthalmol Vis Sci 53: 2360-2367.
19. Bunsen RW, Roscoe HE (1862) Photochemical researches-Part V. On the measurement of the chemical action of direct and diffuse sunlight. Proc R Soc Lond 12: 306-312.
20. Spadea L, Genova LD, Tonti E (2018) Corneal stromal demarcation line after 4 protocols of corneal crosslinking in keratoconus determined with anterior segment optical coherence tomography. J Cataract Refract Surg 44(5): 596-602.
21. Spadea L, Tonti E, Vingolo EM (2016) Corneal stromal demarcation line after collagen cross-linking in corneal ectatic diseases: a review of the literature. Clin Ophthalmol 10: 1803-1810.
22. Kling S, Hafezi F (2017) An algorithm to predict the biomechanical stiffening effect in corneal cross-linking. J Refract Surg 32(2): 128-136.
23. Kling S, Hafezi F (2017) Biomechanical stiffening: Slow low-irradiance corneal crosslinking versus the standard Dresden protocol. J Cataract Refract Surg 43(7): 975-979.
24. Toker E, Cerman E, Oscan DO, Seferoglu OB (2017) Efficacy of different accelerated corneal crosslinking protocols for progressive keratoconus. J Cataract Refract Surg 43(8): 1089-1099.
25. Hammer A, Richoz O, Mosquera SA, Tabibian D, Hoogewoud F, et al. (2014) Corneal biomechanical properties at different corneal crosslinking (CXL) irradiances. Invest Ophthalmol Vis Sci 55(5): 2881-2884.
26. Webb JN, Su JP, Scarcelli G (2017) Mechanical outcome of accelerated corneal crosslinking evaluated by Brillouin microscopy. J Cataract Refract Surg 43(11): 1458-1463.
27. Bao FJ, Zheng YR, Liu C, Zheng X, Zhao Y, et al. (2018) Changes in corneal biomechanical properties with different corneal cross-linking irradiances. J Refract Surg 34(1): 51-58.
28. O’Brart NAL, O’Brart DPS, Aldahlawi, Hayes S, Meek KM (2018) An investigation of the effects of riboflavin concentration on the efficacy of corneal cross-Linking using an enzymatic resistance model in porcine corneas. Invest Ophthalmol Vis Sci 59(2): 1058-1065.