Electro magneto Elastic Actuator for Nanotechnology and Biotechnology

The electro magneto elastic actuator of the piezoeffect, the piezomagnetic effect, the electrostriction or the magnetostriction effect is used for precise alignment in the nanotechnology, the biotechnology and the adaptive optics [1-32]. The piezoactuator on the inverse piezoeffect is serves for the actuation of mechanisms or the management, converts electrical signals into displacement and force [1-8]. The piezoactuator for the nanomechanics is provided the displacement from nanometers to tens of micrometers, a force to 1000N. The piezoactuator is used for research in the nanomedicine and the nanobiotechnology for the scanning tunneling microscopes, scanning force microscopes and atomic force microscopes [14-32].

In the present paper the generalized structural-parametric model and the generalized parametric structural schematic diagram of the electro magneto elastic actuator are constructed by solving the wave equation with the Laplace transform for the equation of the electro magnetolasticity, the boundary conditions on loaded working surfaces of the actuator, the strains along the coordinate axes. The transfer functions and the parametric structural schematic diagrams of the piezoactuator are obtained from the generalized structural-parametric model. In [6,7] was determined the solution of the wave equation of the piezoactuator. In the [14-16,30,31] were obtained the structural-parametric models, the schematic diagrams for simple piezoactuator and were transformed to the structural-parametric model of the electro magneto elastic actuator. The structural-parametric model of the electroelastic actuator was determined in contrast electrical equivalent circuit for calculation of piezoelectric transmitter and receiver [9-12]. In [8,27] was used the transfer functions of the piezoactuator for the decision problem absolute stability conditions for a system controlling the deformation of the electro magneto elastic actuator. The elastic compliances and the mechanical and adjusting characteristics of the piezoactuator were found in [18,21-23,28,29] for calculation its transfer functions and the structural-parametric models. The structural-parametric model of the multilayer and compound piezoactuator was determined in [18-20]. In this paper is solving the problem of building the generalized structural parametric model and the generalized parametric structural schematic diagram of the electro magneto elastic actuator for the equation of electro magneto elasticity.

The general structural-parametric model and the parametric structural schematic diagram of the electro magneto elastic actuator are obtained. In the electro elastic actuator are presented six stress components ^Ti, ^T, ^T3, ^T4,^T,^T6, the components ^Ti - ^T3 are related to extension-compression stresses, ^T4 - ^T to shear stresses. For the electro elastic actuator its deformation corresponds to stressed state. For polarized piezoceramics PZT the matrix state equations [12,14] connected the electric and elastic variables have the form two equations, then the first equation describes the direct piezoelectric effect, the second - the inverse piezoelectric effect.

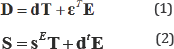
Where D is the column matrix of electric induction; S is the column matrix of relative deformations; T is the column matrix of mechanical stresses; E is the column matrix of electric field strength; s^E is the elastic compliance matrix for E = const; ε^T is the matrix of dielectric constants for T= const; d^t is the transposed matrix of the piezoelectric modules.

The piezoactuator (piezoplate) has the following properties: δ- the thickness, h - the height,b - the width, respectively i = { S, h, b the length of the piezoactuator for the longitudinal, transverse and shift piezoeffect. The direction of the polarization axis P, i.e., the direction along which polarization was performed, is usually taken as the direction of axis 3. The equation of the inverse piezo effect for controlling voltage [6,12] has the form.

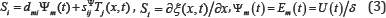
where is the relative displacement of the cross section of the piezoactuator along axis i, Ψ_m (t) is the control parameter along axis m, d_mi is the piezomodule,E_m (t) is the electric field strength along axis m, ^U(^t) is the voltage between the electrodes of actuator,s_ij^Ψ is the elastic compliance, T_jis the mechanical stress along axis j and i, j = 1, 2, ..., 6; m= 1, 2, 3. The main size for the piezoactuator, respectively, the thickness, the height, the width for the longitudinal, transverse, shift piezoeffect. For calculation of actuator is used the wave equation [6,7,12,14] for the wave propagation in a long line with damping but without distortions. After Laplace transform is obtained the linear ordinary second-order differential equation with the parameter p, whereupon the original problem for the partial differential hyperbolic equation of type using the Laplace transform is reduced to the simpler problem [6,13] for the linear ordinary differential equation.

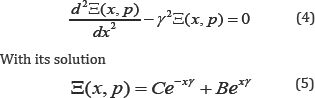
where ( _x, p) is the Laplace transform of the displacement of the section of the piezoactuator, γ = p/c^Ψ + α is the propagation coefficient, c^Ψ is the sound speed for * = const ,is the damping coefficient, Ψ is the control parameter: E for the voltage control, D for the current control, H for the magnet field strength control. From (3, 5), the boundary conditions on loaded surfaces, the strains along the axes the system of equations for the generalized structural-parametric model and the generalized parametric structural schematic diagram Figure 1 of the actuator are determined

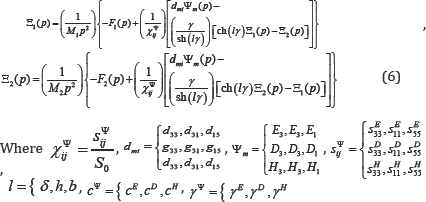
Figure 1: Generalized parametric structural schematic diagram of the electro magneto elastic actuator.

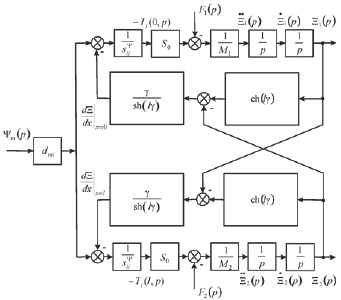
Is the coefficient of the electro magnetolasticity (piezomodule or coefficient of magnetostriction). Figure 1 shows the generalized parametric structural schematic diagram of the electro magneto elastic actuator corresponding to the set of equations (6). The generalized transfer functions of the electro magneto elastic actuator are the ratio of the Laplace transform of the displacement of the face actuator and the Laplace transform of the corresponding control parameter or the force at zero initial conditions. From (6) the generalized matrix equation of the transfer functions of electro magneto elastic actuator.

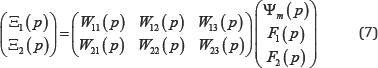
For and the static displacement of the faces of the piezoactuator for the transverse piezoeffect are obtained.

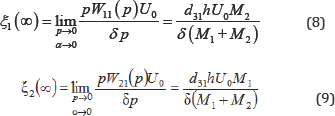
For the piezoactuator from PZT under the transverse piezoeffect at m <1 and m << M₂, d₃₁ = 2.5-10^-13°m/V,h/δ = 20 ,U = 100 V,M₁ = 2 kg andM₂, = 8 kg the static displacement of the faces are determined ξ₁(∞) = 400 nm, ξ₂(∞)= lOOnm, ξ₁(∞)+ξ₂(∞) = 500 nm. For the approximation of the hyperbolic cotangent by two terms of the power series in transfer function (7) the following expressions of the transfer function of the piezoactuator is obtained for the elastic-inertial load at M₁→ ∞, _m << M₂ under the transverse piezoeffect

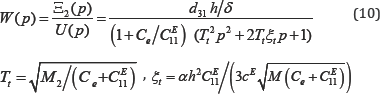
Where U(p) the Laplace is transform of the voltage, T_t is the time constant and ξ_t is the damping coefficient of the piezoactuator. The expression for the transient response of the voltage-controlled piezoactuator for the elastic-inertial load under the transverse piezoeffect is determined.

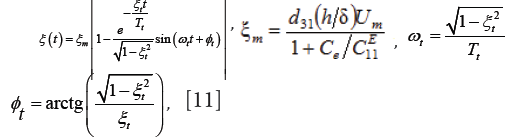
Where ξ_mthe steady-state value of displacement of the piezoactuator is,^um is the amplitude of the voltage. For the voltage-controlled piezoactuator from the piezoceramics PZT under the transverse piezoelectric effect for the elastic-inertial load M₁ →(∞), m << M₂ and input voltage with amplitude U_m = 120 V at d₃₁ = 2.5-10-¹⁰m/V,h/δ = 20,M₂ =4kg, c^E₁₁ = 2.10⁷ N/m,c_e =0.5-10⁷ H/m are obtained values ξ_m=480 nm, T_t = 0.4.1 10^-3c.

The structural-parametric model and parametric structural schematic diagrams of the voltage-controlled piezoactuator for the longitudinal, transverse and shift piezoelectric effects are determined from the generalized structural-parametric model of the electro magneto elastic actuator for the nanotechnology and the biotechnology with the replacement of the generalized parameters. The generalized structural-parametric model, the generalized parametric structural schematic diagram and the matrix equation of the electro magneto elastic actuator are obtained from the solutions of the wave equation with the Laplace transform and from its deformations along the coordinate axes. From the generalized matrix equation for the transfer functions of the electro magneto elastic actuator after algebraic transformations are constructed the matrix equations of the piezoactuator for the longitudinal, transverse and shift piezoelectric effects.

The deformations of the actuator are described by the matrix equation for the transfer functions of the electro magneto elastic actuator for precise alignment in the nanotechnology, the biotechnology, the adaptive optics. The structural-parametric model, the matrix transfer function of the electro magneto elastic actuator is determined. For the control systems in the nanotechnology and the biotechnology. The structural-parametric model, the matrix equation and the parametric structural schematic diagram of the piezoactuator for the transverse, longitudinal, shift piezoelectric effects are obtained from the generalized structural- parametric model of the electro magneto elastic actuator. From the solution of the wave equation, from the equation of the electro magneto elasticity and the deformations along the coordinate axes the generalized structural-parametric model and the generalized parametric structural schematic diagram of the electro magneto elastic actuator are constructed for the control systems for the nanotechnology and the biotechnology.

1. Schultz J, Ueda J, Asada H (2017) Cellular actuators. Butter- worth-Heinemann Publisher, Oxford, UK, p. 382.
2. Uchino K (1997) Piezoelectric actuator and ultrasonic motors, Springer, US, p. 347.
3. Przybylski J (2015) Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering Structures 84(1): 140-151.
4. Ueda J, Secord T, Asada HH (2010) Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Transactions on Mechatronics 15(5): 770-782.
5. Karpelson M, Wei GY, Wood RJ (2012) Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical 176: 78-89.
6. Afonin SM (2006) Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics 73(2): 307-313.
7. Afonin SM (2008) Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady Physics 53(3): 137-143.
8. Afonin SM (2014) Stability of strain control systems of nano-and microdisplacement piezotransducers. Mechanics of solids 49(2): 196-207.
9. Talakokula V, Bhalla S, Ball RJ, Bowen CR, Pesce GL, et al. (2016) Diagnosis of carbonation induced corrosion initiation and progressionin reinforced concrete structures using piezo-impedance transducers. Sensors and Actuators A: Physical 242: 79-91.
10. Yang Y, Tan L (2009) Equivalent circuit modeling of piezoelectric energy harvesters. Journal Of Intelligent Material Systems And Structures 20(18): 2223-2235.
11. Cady WG (1946) Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals, (1st edn), McGraw-Hill Book Company, USA, p. 806.
12. Mason W (1964) Physical Acoustics: Principles and Methods, (1st edn), Academic Press, US, p. 532.
13. Zwillinger D (1989) Handbook of Differential Equations. Academic Press, US, p. 673.
14. Afonin SM (2015) Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. In: Parinov IA (Ed.), Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Nova Science, New York, pp. 225-242.
15. Afonin SM (2016) Structural-parametric model electro magneto elastic actuator nano-and microdisplacement for precision engineering. Precision Engineering. Engineering and Technology 3(6): 110-119.
16. Afonin SM (2016) Structural-parametric models and transfer functions of electro magneto elastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59.
17. Afonin SM (2002) Parametric structural diagram of a piezoelectric converter. Mechanics of solids 37(6): 85-91.
18. Afonin SM (2003) Deformation, fracture, and mechanical characteristics of a compound piezoelectric transducer. Mechanics of solids 38(6): 7882.
19. Afonin SM (2004) Parametric block diagram and transfer functions of a composite piezoelectric transducer. Mechanics of solids 39(4): 119-127.
20. Afonin SM (2005) Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics 50(2): 77-82.
21. Afonin SM (2010) Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids 45(1): 123-132.
22. 22.  Afonin SM (2011) Electromechanical deformation and transformation of the energy of a nano-scale piezomotor. Russian Engineering Research 31(7): 638-642.
23. Afonin SM (2011) Electroelasticity problems for multilayer nano- and micromotors. Russian Engineering Research 31(9): 842-847.
24. Afonin SM (2012) Nano-and micro-scale piezomotors. Russian Engineering Research 32(7-8): 519-522.
25. Afonin SM (2015) Optimal control of a multilayer submicromanipulator with a longitudinal piezo effect. Russian Engineering Research 35(12): 907-910.
26. Afonin SM (2015) Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of Computer and Systems Sciences International 54(3): 424-439.
27. Afonin SM (2006) Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics 74(3): 943-948.
28. Afonin SM (2007) Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids 42(1): 43-49.
29. Afonin SM (2009) Static and dynamic characteristics of a multy-layer electroelastic solid. Mechanics of Solids 44(6): 935-950.
30. Afonin SM (2017) Structural-parametric model electro magneto elastic actuator nanodisplacement for mechatronics. International Journal of Physics 5(1): 9-15.
31. Afonin SM (2017) A structural-parametric model of electroelastic actuator for nano-and microdisplacement of mechatronic system. In: Bartul Z, Trenor J (Eds.), Advances in Nanotechnology, Volume 19, Nova Science, New York, USA, pp. 259-284.
32. Bhushan B (2004) Springer Handbook of Nanotechnology. Springer, New York, p. 1222.

© 2018 Afonin SM. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.