Remarks on Parameters Characterizing the Properties of Porous Materials Used in Biomedicine

Synthetic porous materials play a substantial role in numerous biomedical applications, like tissue engineering, blood rectification, dressing materials design etc. Controlling the structural parameters of pores: their size, form and interconnectivity as well as monitoring the stability of the parameters are important components of the processes of porous material production. On the other hand, some authors pay attention to the influence of structural pores’ parameters on final properties of porous materials, like permeability for fluids and small particles or providing a microenvironment for cells adhesion to the pore walls, their proliferation and differentiation [1-5]. The computer-aided analysis of microscope images of porous materials cross-sections occur to be an effective tool for the assessment of the materials’ characteristics [6]. Among the geometrical and morphological properties, the pore size, non-circularity and their statistical distributions are the most frequently ones taken into consideration [7]. However, it should be remarked that the above-mentioned characteristics usually concern the 2D sections of pores but not the pores as 3D objects themselves. Moreover, the numerical values of geometrical parameters of small objects (like pores) substantially depend on the assumed type of geometry (Euclidean or discrete) and in the case of discrete geometry they also depend on the assumed type of connectivity (4- or 8-connectivity of points on a rectangular grid, typical for computer data processing [8]). Below, some critical remarks concerning numerical characteristics of pores are more exactly presented.

Discrete objects interpretation

Figure 1:Typical microscope image of a porous material cross-section.

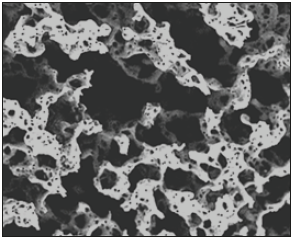
In Figure1 a typical scanning electron microscope (SEM) image of porous material cross-section, subjected to several preliminary operations making easier its computer analysis, is shown. A large variety of pores’ size and irregularity of their form is here remarkable. The problem consists in computer-aided evaluation of selected parameters characterizing the porosity of the given sample of porous material.

One of basic parameters characterizing a porous material is the porosity factor [9]:

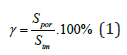
where S_por denotes a total area of visible pore cross-sections, S_im stands for the total image area.

Another important characteristic of a porous material is its porosity histogram χ (S) , defined as a function describing normalized frequency of occurring pores dependently on their size.

Basic measurable geometrical parameters in computer-aided image analysis are length l of lines and surface S of selected 2D objects. For this purpose, some basic concepts of discrete geometry should be used.

Discrete objects are defined as subsets of pixels selected due to their brightness intensity criterion. Points, by definition, are discrete objects represented by pixels not (4- or 8-) connected to any other pixel; lines – by ordered sequences of pixels connected to at most two other pixels of the object. Each 2D object is assumed to be contoured. Contours are defined as lines consisting of pixels belonging to the object and (4- or 8-) connected to at least one pixel not belonging to the given object. Object’s interior consists of object pixels not belonging to its contour.

In any case, a numerical assessment of any geometrical parameter needs a preliminary selection of pixels belonging to the object being of interest. The length l expressed in screen units [su] (which can easily be recalculated into metric units) is defined as the number η₁ of interconnections between the pairs of pixels constituting the line. The surface S, expressed in square screen units [squ], is defined as the sum int 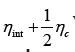where η_int is the number of pixels constituting the object interior while η_c is the number of pixels constituting the contour.

The above given set of assumes is a basis of numerous computer programs of image analysis. However, in some cases they may lead to misunderstandings, as it will be shown below. Figure 2 shows a given configuration of pixels which in different ways should be contoured under the assumption of 4- and 8-connectivity. In the 4-connectivity sense (case a)) the contour consists of 4 disjoin parts whose total length equals 8 [su]. In the 8- connectivity sense (case b)) the contour has the form of a closed line whose length equals 16 [su]. The estimated size (area) in both cases (but only in this example!) is equal: 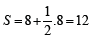[squ] in the case a) and 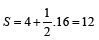[squ] in the case b).

Figure 2:The same discrete object contoured in the sense of:

a) 4-connectivity (contour discontinuous),

b) 8-connectivity

Figure 3:Different interpretations of contours:

a) pixels in circles don’t belong to the contour in the 4-connectivity, belong to it in the 8-connectivity sense,

b) two objects in 4-connectivity, one object in 8-connectivity sense.

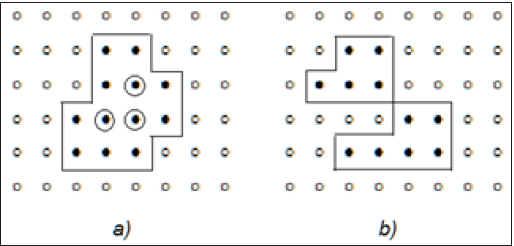
Figure 3 illustrates the case of different interpretation of objects in 4- and 8-connectivity sense. The object shown in (Figure 3a) in the 4-connectivity sense (case I)) contains 4 interior points, while in 8-connectivity sense (case II) it does not contain any interior points. The estimated parameters will then be: case I: l = 6 [su], 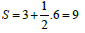[squ]; case II: l = 12, 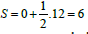[squ]. (Figure 3b) presents: two separate objects in the 4-connectivity or one object in the 8-connectivity sense. Such duality of interpretation may cause substantial differences in results of counting pores and statistical parameters evaluation. Moreover, the effects of size-based classification of pores are strongly dependent on the magnification of the images of porous materials cross-sections.

Shape characterization

Shape is another important pore feature whose evaluation depends on the effects of discrete objects contouring. We are able to visually distinguish the oval, elongated, branched and more complicated shapes of pore cross-sections. For pore characterization numerical shape characteristics are preferred. Among them the smallest rectangle circumscribing the pore crosssection seems to be the simplest and the most convenient one. If d_max and d_min are the lengths of, respectively, the maximal and the minimal side of rectangle, then the ratio:

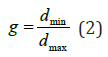
can be established as a compactness coefficient of the rectangle, equal 1 for a square and decreasing to 0 as the rectangle is in one direction up to infinity elongated. The same coefficient can be used to any irregular 2D figure closely circumscribed by the rectangle. However, for this purpose generation of rectangles of any size, position and orientation angle on a plane is necessary. Alas, the notion of a rectangle fully equivalent to this used in Euclidean geometry, in discrete geometry does not exist. Consequently, the above-presented compactness coefficient cannot be used but to characterization the shape of large pores. An alternative possibility to shape of pores parameterization is based on the contour folding concept. It takes the form of a contour folding coefficient expressed by the formula:

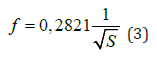
where, once again, l stands for the contour length and S-for object surface. The coefficient f takes value 1 for circles and increases infinitely when contours take more irregular form.

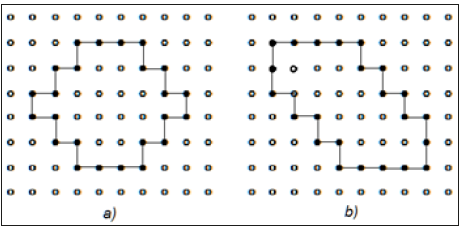
The main critical remark about this concept is caused by the fact that the contour folding coefficients of some different shape objects may be equal, as illustrated by (Figure 4a & 4b). The two objects have the same contour lengths l = 24 [su], surfaces S = [squ] and contour folding coefficients f = 1,382. Remark also that both figures can be inscribed into 7×7 -size squares. Therefore, using this approach, as an auxiliary one to improve shapes discrimination, in this case would be ineffective. Finally, it should be also remarked that magnification of images destined to computer analysis as well as some widely used preliminary image enhancement operations (e.g. noise filtering, morphological closure and/or opening, thresholding, etc. [10]) substantially influence on pore size and visibility.

Figure 4:Two objects of the same size and non-circularity coefficient but different shapes.

Computer-aided image processing methods are an effective tool for evaluation of porous materials properties. However, their effectiveness depends on adequate choosing parameters characterizing pores. In most cases they are based on geometrical parameters, like length of contours or surface of planar crosssections of pores. Numerical values of such parameters in discrete geometry used by computers are not identical to those measured in Euclidean geometry. Moreover, they also depend substantially of the assumed connectivity of points in discrete geometry. This leads to misinterpretations and errors in parametric characterization of pores. For this reason, if any numerical parameters of material porosity resulted from computer-aided analysis are presented, the formal assumptions the corresponding computer program has been based on should be clearly explained. Otherwise, the results can be incomparable. On the other hand, the differences between various methods of porosity parameterization may be inessential if a method (despite of its deficiencies) to control and compare the results reached within a given series of experiments is used.

1. O’Brien FJ, Harley BA, Yannas IV, Gibson LJ (2005) The effect of pore size on cell adhesion in collagen-GAG scaffolds. Biomaterials 26(4): 433-441.
2. Murphy CM, Haugh MG, O’Brien FJ (2010) The effect of mean pore size on cell attachment, proliferation and migration in collagen-glycosaminoglycan scaffolds for bone tissue engineering. Biomaterials 31(3): 461-466.
3. Silva MMCG, Cyster LA, Barry JJA, Yang XB, Oreffo ROC, et al. (2006) The effect of anisotropic architecture on cell and tissue infiltration into tissue engineering scaffolds. Biomaterials 27(35): 5909-5917.
4. Stenhamre H, Nannmark U, Lindahl A, Gatenholm P, Brittberg M (2011) Influence of pore size on the redifferentiation potential of human articular chondrocytes in poly (urethane urea) scaffolds. J Tissue Eng Regener Med 5(7): 578-588.
5. Nuernberger S, Cyran N, Albrecht C, Redl H, Vécsei V, et al. (2011) The influence of scaffold architecture on chondrocyte distribution and behavior in matrixassociated chondrocyte transplantation grafts. Biomaterials 32(4):1032-1040.
6. Chwojnowski A, Przytulska M, Wierzbicka D, Kulikowski J, Wojciechowski C (2012) Membranes’ porosity evaluation by computer-aided analysis of SEM images- a preliminary study. Biocybernetics and Biomed Eng 32(4): 67-75.
7. Wu Q, Wu B (1995) Study of membrane morphology by image analysis of electron micrographs☆. Journal of Membrane Science 105(1-2): 113-120.
8. Russ JC (2011) The image processing handbook. (6^th edn), CRC Press, Boca Raton, Florida, USA.
9. Przytulska M, Kulikowski J (2017) Multi-aspect assessment and classification of porous materials. In: Kurzynski M, et al. (Eds.), Advances in Intelligent Systems and Computing (578), Springer International Publishing AG, Basel, Switzerland, pp. 22-32.
10. Przytulska M, Kulikowski JL, Wierzbicka D (2015) Biomedical images enhancement based on the properties of morphological spectra. Biocybernetics and Biomed Eng 35(3): 206-215.