- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Integrative Journal of Conference Proceedings
Entropy and Fractals
Korablev G А1*, Korablev R G2 and Petrova N G3
1 Department of Physics, Russia
2 Department of Agriculture, Russia
3 Department of Information Security and Communications, Russia
Department of Computer Science & Engineering, Nepal
*Corresponding author:Korablev Grigory Andreevich, Doctor of Science in Chemistry, Professor of the Department of Physics, Russia.
Submission: June 07, 2019;Published: July 09, 2019
Volume1 Issue4July, 2019
Abstract
The resonance stationary state of structural processes takes place under the condition of equality of degrees of corpuscular and wave interactions. The fractal structures are formed under the condition of equilibrium statistic interaction of entropic and negentropic characteristics of all particles. Such principle is realized not only for snowflakes but also in many other natural phenomena, for example, during the cloud formation and even during dust concentration in premises. This condition is also fulfilled in microworld that is confirmed by the equations of Plank’s constant, fine structure constant and for number. The conclusions obtained can be used in practice to search for optimal technological solutions.
Keywords: Spatial-energy parameter; Structural interactions; Entropic nomograms; Laws of thermodynamics; Reversible and irreversible processes; Fractal systems
Introduction
In statistic thermodynamics the entropy (S) of the closed and equilibrious system equals the logarithm of the probability of its definite macrostate [1]
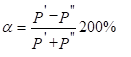
where W-number of available states of the system or degree of the degradation of microstates; k-Boltzmann’s constant. These correlations are general assertions of macroscopic character, do not contain any references to the structure elements of the systems considered and they are completely independent of microscopic models. Therefore, the application and consideration of these laws can result in a large number of consequences. The thermodynamic probability W is the main characteristic of the process. In actual processes in the isolated system the entropy growth is inevitable-disorder and chaos increase in the system; the quality of internal energy goes down. Thermodynamic probability equals the number of microstates corresponding to the given macrostate. An analysis was made of the nature of the change in the value of potential energy by its sign for various potential fields [2].
In the systems in which the interactions proceed along the potential gradient (positive performance) the Lagrangian is performed and the resulting potential energy is found based on the principle of adding reciprocals of the corresponding energies of subsystems [2]. Similarly, the reduced mass for the relative motion of two-particle system is calculated.
In the systems in which the interactions proceed against the potential gradient (negative performance) the algebraic addition of their masses as well as the corresponding energies of subsystems is performed (by the analogy with Hamiltonian). In this investigation the attempt is made to apply such concepts to assess the degree of spatial-energy interactions for fractal systems.
Spatial-energy interactions
The maximum degree of structural interaction evaluated via the coefficient a is determined by the condition of minimum value of a, which represents the relative difference of effective energies of external orbitals of interacting subsystems:
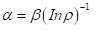(2)
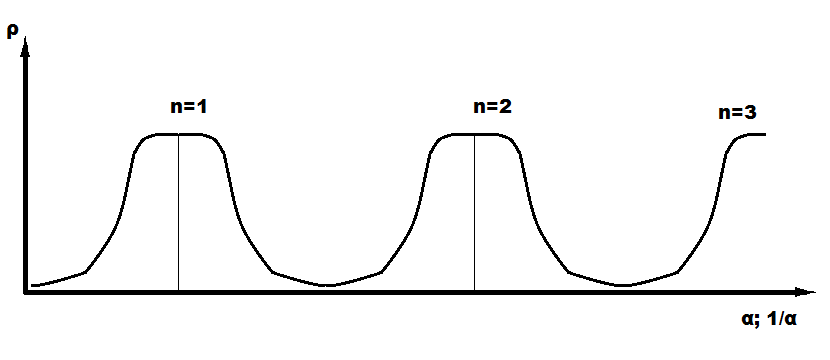
Where P is the spatial-energy parameter, applying reliable experimental data, the dependence nomogram of the degree of structural interactions 𝛒on the coefficient α, the same for a wide class of structures, was obtained (Figure 1). This approach allowed assessing the degree and direction of structural interactions of phase-formation, isomorphism and solubility processes in multiple systems, including the molecular ones [3-10].
Figure 1:Nomogram of structural interaction degree dependence (ρ) on coefficient α.
This type of nomogram and its ambidextrous variant (Figure 2) are widely applied to characterize many processes and phenomena in nature, engineering and even in economy [11-14].
Figure 2:Nomogram of structural interaction degree dependence (ρ) on coefficient 1/α.
Nomogram No 1 can be also displayed [2] in the form of logarithmic dependence
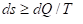(3)
where coefficient β-constant value for this class of structures. β can structurally change mainly within ±5% from the average value. Thus, coefficient α is reversely proportional to the logarithm of the degree of structural interactions and therefore can be characterized as the entropy of spatial-energy interactions of atomic-molecular structures. The more is ρ, the more probable is the formation of stable ordered structures (e.g. the formation of solid solutions), i.e. the less is the process entropy. But also, the less is coefficient α. Conclusion: the relative difference of spatial-energy parameters of the interacting structures can be a quantitative characteristic of the interaction entropy α≡ S.
Entropy in corpuscular-wave processes
In the second law of thermodynamics only those processes are possible in the isolated system, which flow with entropy increase (ds):
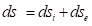(4)
where dQ-change in the heat energy, T- Thermodynamic temperature.
In thermodynamics reversible and irreversible processes are distinguished. Thus, in irreversible expansion the gas transits from less probable to more probable state, i.e. this process flows along the probability gradient. Similarly, the transit of heat from a hotter body to a colder one is irreversible, which also flows along the temperature gradient. As it was already demonstrated, corpuscular interactions also flow along the field gradient. Therefore, it is presumed that the entropy can be a theoretical concept of corpuscular processes.
In the open system there is an interaction with the external environment and general change of the entropy (ds) is expressed by the equation
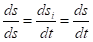
where dsi -changes of the entropy as a result of the processes inside the system on the nomogram number 1, dse change of the entropy conditioned by the interaction with the external environment on the nomogram number 2. Then within the time dt:
Where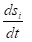 
total velocity of the entropy changes in the closed system, 
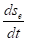entropy products, 
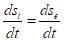entropy flow (negative entropy). For the dynamic stationary state, the total velocity of entropy change must equal zero: ds/dt=0 And then
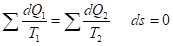(5)
Thus, the entropy products in the stationary state are completely compensated by the negative entropy flow. The processes flowing in an open system are reversible. For example, all mechanical processes without friction belong to them. But there is friction in actual processes, as well as the conversion of mechanical work into heat, and this is already an irreversible process [15]. In the thermal machine there is heat conversion from a colder body to a hotter one. In this case and in all reversible processes the work is performed against the field gradient. And the entropy corresponding to these processes is called negative entropy. As it was demonstrated, the system work against the field gradient corresponds to the wave processes, e.g., in electric field generator.
Such analogy in directed entropic and corpuscular-wave processes allows assuming that the entropy is a theoretical concept of corpuscular interactions, and negative entropy-a concept of wave interactions. Besides, this analogy gives the possibility to use the entropic equation of the stationary state of open systems for the corresponding corpuscular-wave processes. At the same time, the following correlation is fulfilled in the heat machine: At the circular process the increase in the system entropy due to the incoming heat is completely compensated by the decrease in entropy due to the heat output, and the total entropy value equals zero [16]:
(6,7)
As applicable to corpuscular-wave processes, the condition of dynamic stationary state is the condition of equilibrium of their degrees of structural interactions:
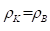(8)
This condition is graphically fulfilled when nomogram No 1 (entropy) is overlapping nomogram No 2 (negative entropy), which gives the following value
Such equality of corpuscular and wave interactions determines the resonance stationary state of the system and it corresponds to the most optimal technological variants. The stationary state is mathematically and graphically fulfilled (Figure1 & 2) by the equation (9).
In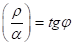
(9)
Thus, e.g., for the constant fine structure this equation is as follows:
In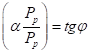 
(10)
Here Pp =WpR=938.2756 МeV х 0.856 fm = 803.107 МeVfm
PeWer=1.43998 МeVfm
-fine structure constant
Pp and Pe-energy parameters of free proton and electron
Pp and Pe- their energy masses
R-dimensional characteristic of proton [17]
r-classical radius of electron
-geodesic angle.
The equation (9) is fulfilled within the accuracy limit of the initial data.
Similarly, for the equation for :
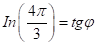
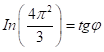(11,12)
The equations (11,12) are fulfilled with the accuracy of up to 1%. But such possible deviations are graphically shown in nomograms No 1 and No 2.
Entropic fractal systems
The main definition of fractal is as follows: “Fractal is the structure consisting of parts, which, in some sense, are similar to the whole” [18]. Fractals are widely manifested in nature. For example, clouds, seashores, bark and crowns of trees. They are also available in structural formations: clusters, polypeptide chains, plasma. The fractal geometry of nature is rather complex and diverse. Its study and modeling are widely introduced in different areas of science and engineering. For example, in the processes of diffusion and adsorption, turbulent flow of liquid, combustion. Based on the fractal definition and from the point of physical chemistry, electrostatically heterogeneous systems are not fractals. Either electrically neutral or similarly charged systems can be the fractals.
Therefore, we can assume that the main condition of fractal formation should be the approximate equality of their corresponding energy characteristics. In this approach the degree of structural interaction is evaluated through the relative difference of energy parameters of particles-coefficient of structural interaction (α) by equation (6). Apparently, many organic structures are formed following this condition polypeptide chains, which can be considered as fractal formations [2,4].
Based on equations (5) and (8) the stable state of each single particle is determined by the condition of equality of its entropic and negentropic components:
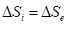(13)
With the statistic aggregation of such particles the entropy of the given particle is in the interaction with the negentropy of the neighboring particle (from one side), and its negentropy interacts with the entropy of the neighboring particle (from another side)-Figure 3 by equations
(14)
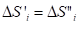(15)
Figure 3:Statistic interaction of entropic and negentropic characteristics; where n-particle number.
In Figure 3 the ascending part of the graph corresponds to negentropy, and the descending one-to entropy. Apparently, the cumulative values of these parameters determine the change in the overall contour of the structure being formed, which can be formally repeated in new bigger fractals. There are different types of fractal curves on the plane (Lévy, Minkowski, Hilbert). Koch curve (Koch snowflake) is especially popular and quoted. Figure 4 demonstrates the step-by-step fractal formation, n-number of stages [19,20]. The triangle (n=1), gradually introduced into the conformation generator, is the initial element of this process. In this approach the lateral sides of the triangle correspond to entropic and negentropic characteristics of the particle itself. In general, Koch curve correlates with the graph of change of entropic characteristics by Figure 3, both by separate small fragments and by bigger formations.
Figure 4:Plotting of Koch curve.
Conclusion
The resonance stationary state of structural processes takes place under the condition of equality of degrees of corpuscular and wave interactions. The fractal structures are formed under the condition of equilibrium statistic interaction of entropic and negentropic characteristics of all particles. Such principle is realized not only for snowflakes but also in many other natural phenomena, for example, during the cloud formation and even during dust concentration in premises.
This condition is also fulfilled in microworld that is confirmed by the equations of Plank’s constant, fine structure constant and for number. The conclusions obtained can be used in practice to search for optimal technological solutions. However, many factors, providing remarkable variety of fractal pictures, still need to be evaluated.
References
1. Gribov LA, Prokofyeva NI (1992) Basics of physics. М Vysshaya shkola, P. 430.
2. Korablev GA (2018) Spatial-energy interactions. Monograph Stary Oskol TNT, p.132.
3. Korablev GA (2012) Activation energy of diffusion of atoms and molecules in biosystems, Bulletin of Kazan Technological University, Russia 5: 133-120.
4. Korablev GA, Zaikov GЕ (2012) Biostructure energy criteria of functional states news of universities. Applied Chemistry and Biotechnology 1(2): 118-124.
5. Korablev GA, Hohryakov NV, Zaikov GЕ, Vasilev YG (2012) The processes of transformation of high-energy bonds in ATP. News of universities. Applied chemistry and biotechnology, Irkutsk State Technical University, Russia 2(3): 114-123.
6. Korablev GA, Petrova NG, Kodolov VI, Korablev RG, Zaikov GЕ (2014) Nomograms of biophysical and economic processes news of universities. Applied Chemistry and Biotechnology 2(7): 48-57.
7. Korablev GA, Zaikov GЕ (2014) Spatial and energy characteristics of photosynthesis news of universities. Applied chemistry and Biotechnology 3(8): 53-66.
8. Korablev GA, Zaikov GE, Khokhriakov NV (2013) Calculation of bond in cluster aqueous nanostructures. journal of characterization and development of novel materials. Nova Science Publishers 5(3-4): 213-218.
9. Korablev GA, Zaikov GЕ (2013) Energy correlations of electron affinity with the values of the spatial-energy parameter. Chemical Physics and Mesoscopy 15(3): 447-456.
10. Korablev GA (2017) On the equations of motion of planets. Successes of Modern Science 1(5): 24-27.
11. Korablev GA, Petrova NG, Zaikov GE (2013) Diversified demonstration of entropy. Nev Book Announcement Nanotechnologies to Nano Industry, USA, P. 120-130.
12. Korablev RG, Petrova NG, Osipov AK, Zaikov GE (2014) Entropy criteria of structural interactions and business quality. Journal of Nature Science and Sustainable Technology 8(3): 461-468.
13. Korablev RG, Maksimov PL, Ktodzinska E, Zaikov GE (2015) Entropic nomograms and S-curves. Monomers, Polymers and Composites Theory and Practical Applications. USA, Pp. 9-21.
14. Korablev GA, Vasil'ev YG, Zaikov GЕ (2015) Hexagonal structures in nano systems. Chemical Physics and Mesoscopy 17(3): 424-429.
15. Chulanovskaya MV (1972) Course of physics for biologists, Leningrad University, Russia, P. 248.
16. Gevorkyan RG, Shepel VV (1972) Course of general physics. Vysshaya shkola, P. 600.
17. Murodyan RM (1977) Physical and astrophysical constants and their dimensional and dimensionless combinations. Fechaya М Atomizdat 8: 175-192.
18. Feder E (1991) Fractals. Moscow, USA, P. 260.
19. https://ru.m.wikipedia.org/wiki/Фрактал.
20. Dresvyannikov AF, Kolpakov ME (2006) Fractals and their applied aspect. Indication method. Kazan State Technological University, Kazan, P. 28.
© 2019 Gajendra Sharma*. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version