- About Us
- Guidelines
-
The Author ensures that the research has been conducted responsibly and ethically with adherence to all relevant regulations. read more..
- For Authors
- For Reviewer
- Manuscript Guidelines
- Membership
-
- Journals
- Reprints
- e-Books
- Videos
- Indexing
- Contact Us
COVID-19
- Submissions
Full Text
Integrative Journal of Conference Proceedings
Energy of Corpuscular-Wave Mechanism
Korablev GА*
Doctor of Chemical Sciences, Russsia
*Corresponding author:GА Korablev, Doctor of Chemical Sciences, Russsia
Submission: March 06, 2019;Published: March 21, 2019
Volume1 Issue2March, 2019
Abstract
On the basis of the first law of thermodynamics, an analysis of the orientation of structural interactions was carried out. In the systems in which the interaction proceeds along the potential gradient (positive work), the resultant potential energy is found based on the principle of adding reciprocals of corresponding energies of subsystems-there is a corpuscular mechanism. In the systems in which the interactions proceed against the potential gradient (negative performance) the algebraic addition of their masses, as well as the corresponding energies of subsystems is performed-there is a wave mechanism. Act of quantum action expressed via Plank’s constant is narrowed to the energy equilibrium-exchange redistribution between the corpuscular and wave processes, that is demonstrated via the angular vector of such motion. Energy characteristics of functional states of bio-systems are defined basically by P-parameter values of atom first valence electron. The principles of stationary biosystem formation are similar to the conditions of wave processes in the phase. Under the condition of the minimum of such interactions, the pathological (but not stationary) biostructures containing the molecular hydrogen can be formed.
Keywords: Potential gradient; Corpuscular-wave dualism; Spatial-energy parameter; Biosystems; Stationary and pathological states
Introduction
To obtain the dependence between energy parameters of free atoms and degree of structural interactions in simple and complex systems is one of strategic tasks in physical chemistry. Classical physics and quantum mechanics widely use Coulomb interactions and their varieties for this. Thus in [1] Van der Waals, orientation and charge-dipole interactions are referred to electron-conformation interactions in bio-systems. And as a particular case exchange-resonance transfer of energy. But biological and many cluster systems are electroneutral in structural basis. And non-Coulomb equilibrium-exchange spatial-energy interactions, i.e. non-charge electrostatic processes, are mainly important for them. The structural interactions of summed electron densities of valence orbitals of corresponding conformation centers take place-processes of equilibrium flow of electron densities due to overlapping of their wave functions. Heisenberg & Dirac [2] proposed the exchange Hamiltonian derived in the assumption on direct overlapping of wave functions of interacting centers: H =Iο S1 S2 = where: H – spin operator of isotropic exchange interaction for pair of atoms, Iο – exchange constant, S1 and S2 –overlapping integrals of wave functions. In this model electrostatic interactions are modeled by effective exchange Hamiltonian acting in the space of spin functions. In particular, such approach is applied to the analysis of structural interactions in cluster systems. It is demonstrated in Anderson’s works [3] that in compounds of transition elements when the distance between paramagnetic ions considerably exceeds the total of their covalent radii, “super-exchange” processes of overlapping cation orbitals take place through the anion between them. In this work similar equilibrium-exchange processes are evaluated through the notion of spatial-energy parameter-Р-parameter. On two principles of adding energy characteristics of interactions The analysis of kinetics of various physical and chemical processes shows that in many cases the reciprocals of velocities, kinetic or energy characteristics of the corresponding interactions are added. And also: “From classical mechanics it is known that the relative motion of two particles with the interaction energy U(r) takes place as the motion of material point with the reduced mass μ:
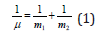
in the field of central force U(r), and general translational motion-as a free motion of material point with the mass:
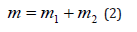
Such things take place in quantum mechanics as well” [4].
For moving thermodynamic systems the first commencement of
thermodynamics is as follows: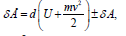
where: δÅ-amount of energy transferred to the system; element
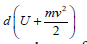-characterizes the changes in internal and kinetic energies of
the system; +δÀ -work performed by the system; −δÀ-work
performed with the system. As the work value numerically equals
the change in the potential energy, then:
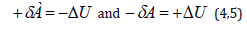
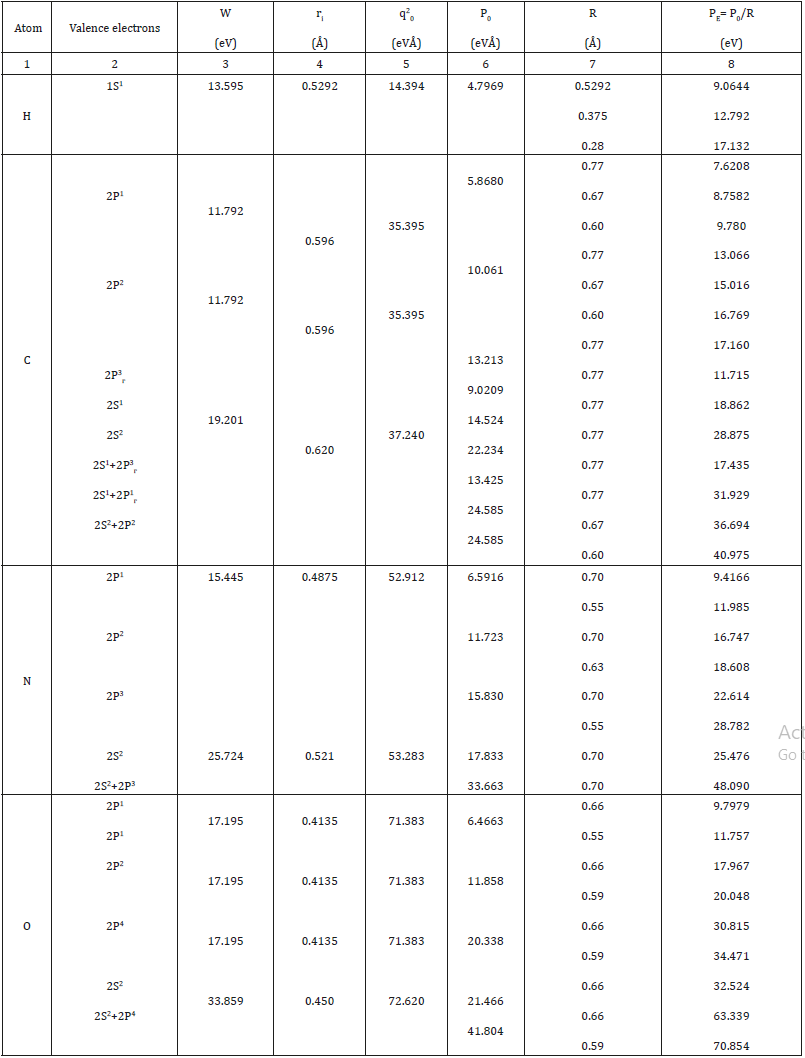
Table 1:Directedness of the interaction processes.
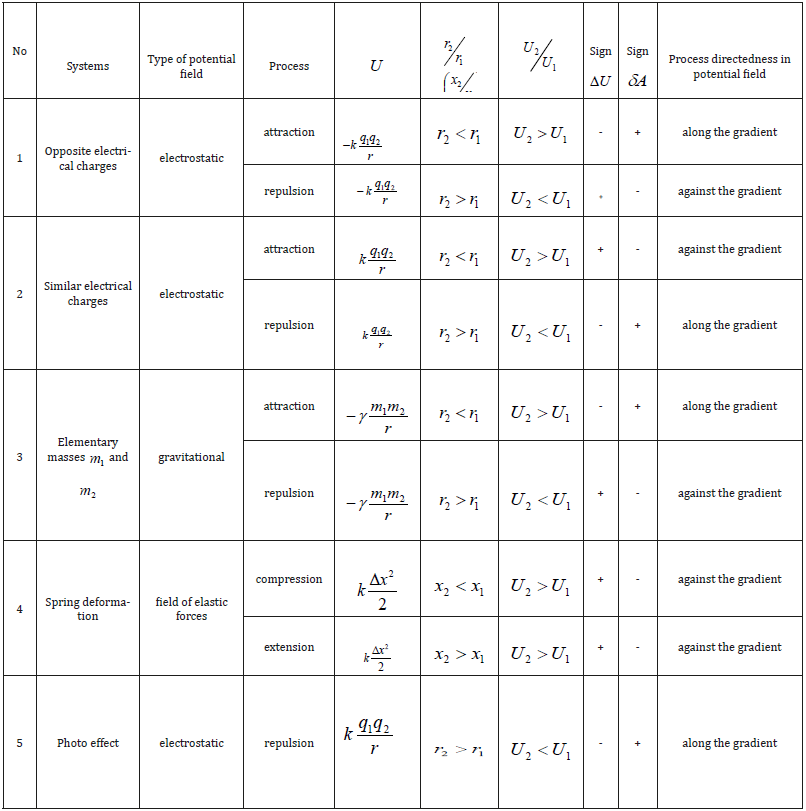
The character of the change in the potential energy value (ΔU) was analyzed by its sign for various potential fields and the results are given in Table 1. From the table it is seen that the values –ΔU and accordingly +δA (positive work) correspond to the interactions taking place along the potential gradient, and ΔU and −δA (negative work) occur during the interactions against the potential gradient. The solution of two-particle task of the interaction of two material points with masses m1 and m2 obtained under the condition of the absence of external forces, corresponds to the interactions flowing along the gradient, the positive work is performed by the system (similar to the attraction process in the gravitation field).
The solution of this equation via the reduced mass (μ ) is the Lagrangian equation for the relative motion of the isolated system of two interacting material points with masses m1 and m2, which in coordinate х is as follows:
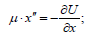
Here: U-mutual potential energy of material points; μ -reduced mass. At the same time, х″=a (feature of the system acceleration). For elementary portions of the interactions Δх can be taken as follows:
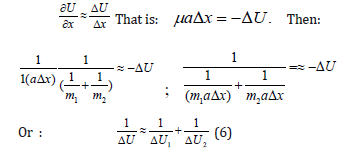
where 1 ΔU and 2 ΔU -potential energies of material points on the elementary portion of interactions, ΔU -resulting (mutual) potential energy of these interactions.
Thus:
A. In the systems in which the interactions proceed along the potential gradient (positive performance) the resulting potential energy is found based on the principle of adding reciprocals of the corresponding energies of subsystems [5]. Similarly, the reduced mass for the relative motion of two-particle system is calculated.
B. In the systems in which the interactions proceed against the potential gradient (negative performance) the algebraic addition of their masses, as well as the corresponding energies of subsystems, is performed (by the analogy with Hamiltonian).
Spatial-energy parameter (P-parameter)
From the equation (6) it is seen that the resulting energy
characteristic of the system of two material points interaction
is found based on the principle of adding reciprocals of initial
energies of interacting subsystems. “Electron with mass m moving
near the proton with mass М is equivalent to the particle with mass:
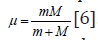Therefore, when modifying the equation (6), we can
assume that the energy of atom valence orbitals (responsible for
interatomic interactions) can be calculated [5] by the principle of
adding reciprocals of some initial energy components based on the
following equations:
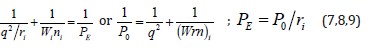
Here: Wi-electron orbital energy [7]; ri -orbital radius of i–orbital [8]; q = Z * /n*9 1 , ni-number of electrons of the given orbital, Z* and n*-nucleus effective charge and effective main quantum number, r-bond dimensional characteristics. Р0 was called spatial-energy parameter (SEP), and РE-effective Р-parameter (effective SEP). Effective SEP has physical sense of some averaged energy of valence electrons in the atom and is measured in energy units, e.g. electronvolts (eV). The values of Р0-parameter are tabulated constants for the electrons of the given atom orbital. For dimensionality SEP can be written down as follows:
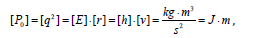
where [E], [h] and [υ]-dimensions of energy, Planck’s constant and velocity. Thus Р-parameter corresponds to the processes going along the potential gradient.
The introduction of Р-parameter should be considered as further development of quasi-classical notions using quantummechanical data on atom structure to obtain the criteria of energy conditions of phase-formation. At the same time, for the systems of similarly charged (e.g.-orbitals in the given atom), homogeneous systems the principle of algebraic addition of such parameters is preserved:
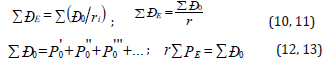
Here Р-parameters are summed on all atom valence orbitals (Table 2). According to the established rule [5] of adding P-parameters of similarly charged or homogeneous systems for two orbitals in the given atom with different quantum characteristics and according to the energy conservation rule we have:
Table 2:Р-parameters of atoms calculated via the electron bond energy.
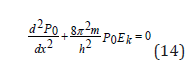
where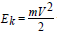 
electron kinetic energy. Schrodinger equation for the stationery
state in coordinate х:
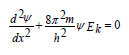
When comparing these two equations, we see that Р0-parameter numerically correlates with the value of Ψ-function: 0 Ð ≈ Ψ and is generally proportional to it: Р0~Ψ. Taking into account the broad practical opportunities of applying the P-parameter methodology, we can consider this criterion as the materialized analog of Ψ-function. Since Р0-parameters like Ψ-function have wave properties, the superposition principles should be fulfilled for them, defining the linear character of the equations of adding and changing P-parameter.
Structural exchange spatial-energy interactions
In the process of solid solution formation and other structural equilibrium-exchange interactions the single electron density should be set in the points of atom-component contact. This process is accompanied by the redistribution of electron density between the valence areas of both particles and transition of the part of electrons from some external spheres into the neighboring ones. Apparently, the frame atom electrons do not take part in such exchange. Obviously, when electron densities in free atomcomponents are similar, the transfer processes between boundary atoms of particles are minimal; this will be favorable for the formation of a new structure. Thus, the evaluation of the degree of structural interactions in many cases means the comparative assessment of the electron density of valence electrons in free atoms (on averaged orbitals) participating in the process, which can be correlated with the help of P-parameter model. The less is the difference (Р›0/r’i-P”0/r”i), the more favorable is the formation of a new structure or solid solution from the energy point. In this regard, the maximum total solubility, evaluated via the coefficient of structural interaction α, is determined by the condition of minimum α value, which represents the relative difference of effective energies of external orbitals of interacting subsystems:
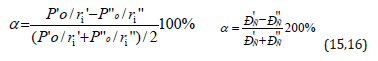
where РS-structural parameter found by the equation:
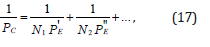
Table 3:Structural РC-parameters calculated via the electron bond energy.
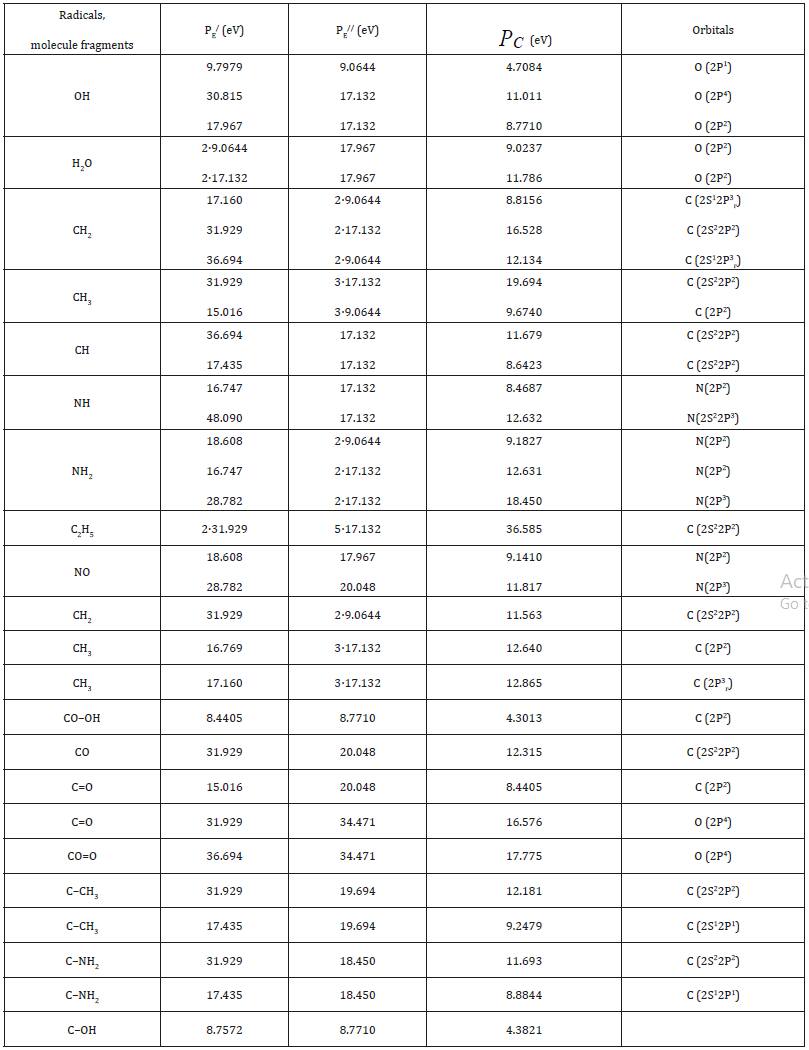
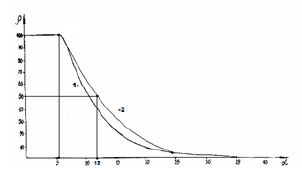
here N1 and N2-number of homogeneous atoms in subsystems. (Table 3). Applying the reliable experimental data we obtain the nomogram of structural interaction degree dependence (ρ ) on coefficient α , the same for a wide range of structures (Figure 1). This approach gives the possibility to evaluate the degree and direction of the structural interactions of phase formation, isomorphism and solubility processes in multiple systems, including molecular ones.
Corpuscular-wave mechanism
The formalism of the equations (7,8,17) is not principally new. Already in 1924 the following equation was obtained based on Compton’s effect:
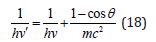
Here: hν’-energy of scattered photon, hν-energy of incident photon, mc2-own energy of electron, ϴ-scattering angle. At the same time, the energy of photons decreases by the value additionally obtained by the electron. In this way the act of quantum action takes place, resulting in the energy redistribution between the corpuscular and wave properties of the interacting systems.
In this process, the same as in photo effect, the interaction proceeds along the potential gradient and the work is positive. During the quantum transitions in the atom the similarly charged particles (electrons) interact by irradiation, i.e., by the wave process. At the same time, for dissimilarly charged particles (electrons and nucleus of atoms) the process goes along the potential gradient, i.e., the corpuscular mechanism is realized. It is known that a particle can have three main motions: translational, rotational and oscillatory. But quantum mechanics does not consider the issue of electron trajectory as we can speak only of the possibility of its location in the given point in space.
But an electron also moves if this translational motion goes along the potential gradient, then it corresponds to corpuscular process, and rotational motion-to wave one. Electric current is the motion of electrons along the potential gradient. If we assume that the magnetic field generated by it is the wave process, there have to be ratio between the electric and magnetic constants. The difference of phases of electric and magnetic oscillations in electromagnetic wave is π/2.
Having introduced the coefficient (2/π)^2, we have the equation for Plank’s constant with the accuracy close to the initial data themselves:
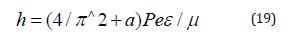
Here а=0.0023293-experimental quantum correction to spingsfactor of the electron, ɛ-electric constant, μ-magnetic constant, h-Plank’s constant. For a free electron Pе=Wr, where W=0.510034 МeV=0.81872˟10-13J. The value of classical radius of electron r=2.81794˟10-15m was used as the dimensional characteristic and, therefore, Ре=2.30712˟10-28Jm. The proportionality coefficient in the equation (19) has the velocity dimensionality (m/sec) for the ratio (F/Hn), i.e. in such way the rate of energy redistribution in the system “particle-wave” is characterized.
Therefore, the act of quantum action expressed via Planck’s constant is narrowed to the energy equilibrium-exchange redistribution between the corpuscular and wave processes. Generalizing the formalism of the equations (7,8,17) onto all other interactions flowing along the potential gradient, we can make the conclusion that corpuscular processes take place in these cases, and wave dualism corresponds to the interactions against the potential gradient.
Corner angles
Let us consider some macroprocesses important in this case. The silkworm winds the natural (organic) silk thread only at a definite rotation angle. In cosmonautics the cellulose-viscose thread is wound around the metal cylinder of the spaceship following the special technology, and, what is important, at the same winding angle as the silkworm. The spaceship becomes most durable, more technologically high-quality and lighter [9-13]. We can also speak of other examples of such phenomenon.
This angle (mainly as applicable to organic systems) was called the geodesic angle: φg = 54.73º=54º44’. The notions of breaking stress in the process of plastics stretching by its winding pitch are used in papers [12,13]: σα-axial, σβ-circumferential stress, which are replaced by the value Nα-axial “effort” and Nβ-circumferential “effort” proportional to them. At the same time, the following equation is fulfilled:
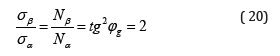
“This condition allows obtaining the equally tensioned system of threads with the minimal item weight”13.
Thus, the rotation angle numerically determines the ratio of two legs of the triangle, whose values characterize energy and dependencies in the system with quantum and wave processes through axial and circumferential stresses.
All this is broadly demonstrated in macro- and micro-processes. Below are some examples.
A. Characteristic of spin-orbital interaction-constant of fine structure α=r/λ, where r-classical radius of electron, λ-its Compton wavelength.
B. Formally, but similarly: the interaction force of two long conductors with current is proportional to the ratio l/2πr, where l-length of conductors, r-distance between them.
C. π equals the ratio of circumference length to its diameter.
In quantum mechanics the ratio of magnetic moment to its mechanical moment is called the magneto mechanic ratio-g. At the same time, gs=2, if the electron magnetic moment is conditioned only by the spin component, and g=1, if it is produced by the orbital motion of electrons. Their ratio gs/g=2, the same as tg2φг =2, characterize the existing corpuscular-wave dependencies. The ratios of the sides of the right triangle were used as the basis of the well-known Babylonian Table written thousands of years ago. It is this table, and obviously, its principle of equally stressed-strained systems were applied in the technology of unique construction, which still remains a puzzle. In these examples, as in many others, such approach allows evaluating structural interactions based on corpuscular and wave dependencies in each action act, e.g., in the equation of dependence of rotational and orbital motion of planets [14]. Using the algorithm in the ratio ρ/α to obtain the linear dependence with the rotation angle φ and in accordance with the equation (20) we have:
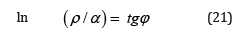
In homogeneous systems with the closeness of values of their P-parameters (wave process) if α→0, then tgφ→∞ and φ=90°. In the corpuscular mechanism of interaction if α→∞, then tg α→0, and φ=0. In general case, in the system “particle-wave” the rotation angle φ changes from 0° (at ρ=0%) up to 90° (at ρ=100%). It can be assumed that equally strained system is obtained under the condition of approximate equality of corpuscular and wave parameters, i.e. at the geodesic angle ρ=50%. Then the calculation of the coefficient α by the equation (21) gives 12.16%, approximately corresponding to the coordinates obtained in nomogram in Figure 1. Similar types by this nomogram and its reverse-reading variants are the graphic characteristics of many phenomena and processes in nature, engineering and economy. Therefore, such S-curves have been called “Lines of life”.
Figure 1:Nomogram of structural interaction degree dependence (ρ) on coefficient α Here curve 2-for biosystems.
Bio-structural energy criteria of functional states
Isomorphism as a phenomenon is usually considered as applicable to crystal structures. But, obviously, similar processes can also flow between molecular compounds, where the bond energy can be evaluated via the relative difference of electron densities of valence orbitals of interacting atoms. Therefore the molecular electronegativity is quite easily calculated via the values of the corresponding P-parameters. Since Р-parameter possesses wave properties (Similar to Ψ’-function), mainly the regularities in the interference of the corresponding waves should be fulfilled. The interference minimum, oscillation weakening (in anti-phase) takes place if the difference in wave move (Δ) equals the odd number of semi-waves:
where n = 0, 1, 2, 3, … (22)
The difference in wave move (Δ) for Р-parameters can be
evaluated via their relative value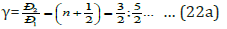 
Interference maximum, oscillation enhancing (in phase) takes place if the difference in wave move equals an even number of semiwaves:
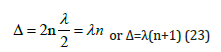
As applicable to P-parameters, the maximum enhance of interaction in the phase corresponds to the interactions of similarly charged systems or systems homogeneous by their properties and
functions (e.g. between the fragments or blocks of complex organic structures, such as CH2 and NNO2).And then: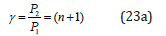
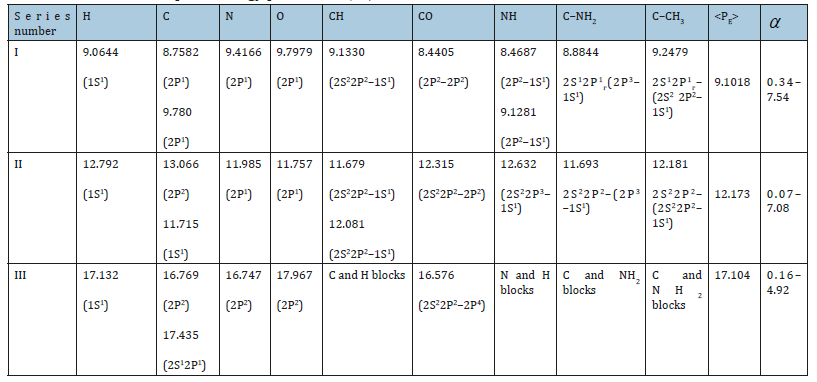
It was shown [15] that the molecular negativity is numerically equal to the P-parameter of the first valence electron divided by 3. Hydrogen atom, element No 1 with orbital 1S [1] defines the main energy criteria of structural interactions (their “ancestor”). Table 1 shows its three PE-parameters corresponding to three different characteristics of the atom. R1=0.5292 А0-orbital radiusquantum- mechanical characteristic gives the initial main value of PE-parameter equaled to 9.0644eV;
R2 = 0.375 А0-distance equaled to the half of the bond energy in Н2 molecule. But if hydrogen atom is bound with other atoms, its covalent radius is ≈ 0.28А0. In accordance with equation (23а) P2 = P1 (n+1), therefore P1 ≈ 9.0644eV, P2 ≈ 18.129eV. These are the values of possible energy criteria of stable (stationary) structures. The dimensional characteristic 0.375 А0 does not satisfy them, therefore, there is a transition onto to the covalence radius ≈ 0.28 А0, which provides the value of P-parameter approximately equaled to P2.
It was shown earlier [5] that the condition for the formation of stable structures is an approximate equality of the P-parameter of the subsystems. From a big number of different combinations of interactions we can obtain series with approximately equal values of P-parameters of atoms (or radicals). Such series, by initial values of hydrogen atom, are given in Table 4 (at α < 7.5%). First series for PE=9.0644eV-the main, initial, where Н, С, О, N atoms have PE- parameters only of the first electron and interactions proceed in the phase. Second series for Р›E = 12.792eV is the non-rational, pathological as it more corresponds to the interactions in antiphase: by equation (22а) Р››E=13.596eV. Coefficient α between the parameters Р›E and Р››E equals 6.1%, thus defining the possibility of forming “false” biostructures containing the molecular hydrogen Н2. Coefficient α between series I and II is 34.1%, thus confirming the irrationality of series II. Third series for Р›E = 17.132eV-stationary as the interactions are in the phase: by equation (22а) Р››E = 18.129eV (α =5.5%). Specific local energy effects (electromagnetic fields, radiation, etc.) upon structural conformations can increasingly follow the pathological series II. Isn’t it one of the reasons of normal functioning failure in biosystems, e.g., in oncological diseases? If so, some practical recommendations can be done, which come down to the necessity of converting the molecular hydrogen into the atomic one, e.g., through the interaction with hydroxyl OH group.
From Table 4 it is seen that the majority of atoms and radicals, depending on the bond types and bond lengths, have PE-parameters of different series. When introducing the stem cells, it is important for the molecular hydrogen not to be present in their structures.SSSS Otherwise atoms and radicals can transfer into the series II and disturb the vital functions of the main first system. The reverse method can be applied to utilize polymeric materials transferring their molecular fragments into the pathological series II.
Table 4:Bio structural spatial-energy parameters (eV).
Conclusion
It is demonstrated that corpuscular interactions flow along the potential gradient (principle of adding reciprocals of energies), and wave processes-against the potential gradient (principle of algebraic addition of energies). Р-parameters of the first valence electron of atoms define the energy characteristics of stationary states (in normal state) under the condition of the maximum of wave processes. Under the condition of the minimum of such interactions, the pathological (but not stationary) biostructures containing the molecular hydrogen can be formed.
References
- Rubin AB (1987) Theoretical biophysics. In: Vysshaya shkola (ed) Biophysics, p. 319.
- Dirac PA (1935) Quantum Mechanics, London, Oxford Univ Press, USA.
- Anderson PW (1963) In Magnetism, Academic Press, USA 1: 25.
- Blokhintsev DI (1961) Basics of quantum mechanics. In: Vysshaya shkola M (ed.), p. 512.
- Korablev GA (2005) Spatial-energy principles of complex structures formation, Brill Academic Publishers, Netherlands, p. 426.
- Eyring G, Walter J, Kimball G (1948) Quantum chemistry, p. 528.
- Fischer CF (1972) Atomic data 4: 301-399.
- Waber JT, Cromer DT (1965) J Chem Phys 42(12): 4116-4123.
- Clementi E, Raimondi DL (1963) Atomic Screening constants from S C F Functions. J Chem Phys 38(11): 2686-2689.
- Korablev GA, Kodolov VI, Lipanov AM (2004) Analog comparisons of lagrange and hamilton functions with spatial-energy parameter. Chemical Physics and Mesoscopy 6(1): 5-18.
- Pidgainy M, Morozova VM, Dudko VA (1967) Methodology for calculating characteristics of geodesic winding of shells of rotational bodies. Mechanics of Polymers 6: 1096-1104.
- Ayushev T (2005) Geometric aspects of adaptive technology of producing structures by winding from fibrous composite materials. Ulan-Ude: BNC SO RAS Publishers, Russia, p. 212.
- Kodolov VI (1992) Polymeric composites and technology of producing aircraft engines from them. Izhevsk Mechanical Institute, Russia, p. 200.
- Korablev GA (2017) On dynamics of rotational motions in macro- and microsystems. European Chemical Bulletin, Budapest 6(2): 79-82.
- Korablev GA (2016) Spatial-energy parameter and its application in research. Lap Lambert Academic Publishing. Germany, pр. 1-65.
© 2019 Korablev GА. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and build upon your work non-commercially.
Editor In Chief
.jpg)
Signup for Newsletter
Quick Links
Editorial Board Registrations
Submit your Article
Best Paper of the Volume
Reprints
Refer a Friend
Advertise With UsOur Recent Edition
.jpg)
Top Editors
.jpg)
.bmp)
.jpg)
.png)
.jpg)
.png)
.png)
.png)
Financial Support
Sponsors
Latest e-Books
Latest Video
a Creative Commons Attribution 4.0 International License. Based on a work at www.crimsonpublishers.com.
Best viewed in 
| Above IE 9.0 version